Euclid’s approach to geometry is commonly described as axiomatic. What does this term mean and is it justified?
In his introduction to Euclid, Thomas Heath quotes a lengthy passage from Aristotle’s Posterior Analytics, which he considers a full and lucid description of an axiomatic system. Taking a leaf out of Heath’s book, I include here a summary of Aristotle’s thesis:
§ 1 All teaching and all intellectual learning come about from already existing knowledge. This is evident if we consider it in every case; for the mathematical sciences are acquired in this fashion, and so is each of the other arts. And similarly too with arguments—both deductive and inductive arguments proceed in this way; for both produce their teaching through what we are already aware of ...
§ 2 ... it is necessary for demonstrative understanding in particular to depend on things which are true and primitive and immediate and more familiar than and prior to and explanatory of the conclusion ... Depending on things that are primitive is depending on appropriate principles; for I call the same thing primitive and a principle. A principle of a demonstration is an immediate proposition, and an immediate proposition is one to which there is no other prior.
§ 3 ... neither is all understanding demonstrative, but in the case of the immediates it is non-demonstrable—and that this is necessary is evident; for if it is necessary to understand the things which are prior and on which the demonstration depends ... it is necessary for these immediates to be non-demonstrable ...
§ 4 ... Demonstration, therefore, is deduction from what is necessary ...
§ 6 Now if demonstrative understanding depends on necessary principles (for what one understands cannot be otherwise), and what belongs to the objects in themselves is necessary ... it is evident that demonstrative deduction will depend on things of this sort ...
§ 10 I call principles in each genus those which it is not possible to prove to be. Now both what the primitives and what the things dependent on them signify is assumed; but that they are must be assumed for the principles and proved for the rest—e.g. we must assume what a unit or what straight and triangle signify, and that the unit and magnitude are; but we must prove that the others are. (Barnes 2-14, Posterior Analytics 71a1-76a37)

The axiomatic method, therefore, is one in which certain primitive assumptions—axioms—are postulated without proof, while the remaining propositions of the theory are deduced as logical consequences of these axioms. Axioms must be assumed without proof, because every proof relies on premises. If these premises are assumed without proof, then they are our axioms, and we have simply replaced one set of axioms with another. If, on the other hand, the premises have been proved, then the same argument applies to the premises of those proofs. And so on ad infinitum. Aristotle was aware that we must start with unproven axioms if we are to avoid such an infinite regress:
§ 3 Now some think that because one must understand the primitives there is no understanding at all; others that there is, but that there are demonstrations of everything. Neither of these views is either true or necessary. For the one party, supposing that one cannot understand in another way, claim that we are led back ad infinitum on the grounds that we would not understand what is posterior because of what is prior if there are no primitives; and they argue correctly, for it is impossible to go through infinitely many things. And if it comes to a stop and there are principles, they say that these are unknowable since there is no demonstration of them, which alone they say is understanding ... (Barnes 5-6, Posterior Analytics 72b5-72b12)
Aristotle believed that a primitive could be understood without the necessity of a proof:
But we say that neither is all understanding demonstrative, but in the case of the immediates it is non-demonstrable—and that this is necessary is evident; for if it is necessary to understand the things which are prior and on which the demonstration depends, and it comes to a stop at some time, it is necessary for these immediates to be non-demonstrable. So as to that we argue thus; and we also say that there is not only understanding but also some principle of understanding by which we become familiar with the definitions. (Barnes 6, Posterior Analytics 72b19-72b24)

Euclid begins the Elements by stating without proof:
23 Definitions
5 Postulates
5 Common Notions
According to Euclid’s 5th-century commentator Proclus:
... it was incumbent on [Euclid] to set apart the principles from their consequences; and this is just what Euclid does in practically every book, besides setting forth at the outset of his whole treatise the common principles of the science. Next he divides them into hypotheses, postulates, and axioms, for these are all different from each other. [Translator’s Footnote: Note that Proclus describes Euclid as dividing the κοιναὶ ἀρχαί [common principles] of geometry into ὑποθέσεις [hypotheses], αἰτήματα [postulates], and ἀξιώατα [axioms] instead of the ὅροι [definitions], αἰτήματα, and κοιναὶ ἔννοιαι [common notions] of our Euclid text.] ... When a proposition that is to be accepted into the rank of first principles is something both known to the learner and credible in itself, such a proposition is an axiom: for example, that things equal to the same thing are equal to each other. when the student does not have a self-evident notion of the assertion proposed but nevertheless posits it and thus concedes the point to his teacher, such an assertion is a hypothesis [definition]. That a circle is a figure of such-and-such a sort we do not know by a common notion in advance of being taught, but upon hearing it we accept it without a demonstration. Whenever, on the other hand, the statement is unknown and nevertheless taken as true without the student’s conceding it, then, he says, we call it a postulate: for example, that all right angles are equal. (Morrow 62-63)
Most scholars can appreciate the distinction between a definition and an axiom. Definitions are somewhat arbitrary and up to the mathematician: Euclid can define anything he likes in whatever way he likes, and we just have to accept it as part of his system. Axioms, on the other hand, are generally thought to be objectively true—possibly, even, obviously true.
But in what sense do Euclid’s postulates differ from his common notions? Proclus again:

The first principles of geometry are divided into three groups: hypotheses [definitions], postulates, and axioms [common notions] ... now let us examine particularly and more precisely the distinction between postulates and axioms ... Hypotheses, or what are called definitions, we have considered in the foregoing ...
It is a common character of axioms and postulates alike that they do not require proof or geometrical evidence but are taken as known and used as starting-points for what follows ... axioms take for granted things that are immediately evident to our knowledge and easily grasped by our untaught understanding, whereas in a postulate we ask leave to assume something that can easily be brought about or devised, not requiring any labor of thought for its acceptance nor any complex construction. Hence clear knowledge without demonstration and assumption without construction distinguish axioms and postulates ... (Morrow 140-141)
In other words:
Common Notions are axioms that do not require proof because they are self-evidently true.
Postulates are axioms that Euclid chooses not to prove, because he has to start from somewhere if he wishes to avoid Aristotle’s infinite regress.
Note that Euclid’s common notions are somewhat controversial. In Theon of Alexandria’s edition, there were nine common notions:
Of the usual Common Notions Heiberg left out one without comment; he bracketed three others, thereby ascribing to them a doubtful status; and he later declared another one to be definitely an interpolation (thus leaving five). T. L. Heath in his edition of The Elements gives the five Postulates and the remaining five Common Notions; these are also precisely the Postulates and Common Notions that Proclus accepts in his Commentary on Book I. Nevertheless Heath considered it probable that Common Notions 4 and 5 were interpolations; and P. Tannery maintained that none were authentic. (Seidenberg 264)
In the Latin translation which Heiberg appended to his critical edition of Euclid’s text, only the five currently accepted common notions are given (numbered by Heiberg I, II, III, VII and VIII (Heiberg 11).
Note also that in the course of the Elements, Euclid introduces a further 108 definitions, making a total of 131. He does not, however, introduce any further postulates or common notions.

Axiomatic System?
It is a commonplace that Euclid’s Elements constitutes an axiomatic system. But is this true? Curiously, there are some scholars who reject this position. One of these was the American mathematician Abraham Seidenberg:
Historians are fond of repeating that Euclid developed geometry on an axiomatic basis, but the wonder is that any mathematician who has looked at The Elements would agree with this. Anyone who looks at The Elements with modern hindsight sees that something is wrong; but we have all been told in our childhood that Euclid had the axiomatic method, so the usual reaction is to speak of “gaps”. The word is hardly right, though, if there was nothing there in the first place. (Seidenberg 263)
Seidenberg concedes that Eudoxus of Cnidus’s Doctrine of Magnitude, which Euclid presents in Book 5 of the Elements, is a good example of an axiomatic system. But, he argues, the method followed by Euclid in Book 1 is fundamentally different. This is particularly clear in the case of Proposition 4 (Elements 1.4), which is the first true theorem in the book. This is the famous SAS (Side-Angle-Side) Theorem, in which it is proved that two triangles ABC and DEF are congruent (equal) if two sides (AB, AC) and the included angle (BAC) of one of the triangles are equal in measure to the respective sides (DE, DF) and angle (EDF) of the other triangle. In proving this theorem, Euclid requires us to “apply” one of the triangles to the other. That is to say, we must “pick up” one of the triangles and superimpose it on the other triangle so that the vertices A and D coincide, with the side AB lying along the side DE. Euclid then shows that the other vertices will also coincide (B with E, C with F), demonstrating that the triangles are equal:
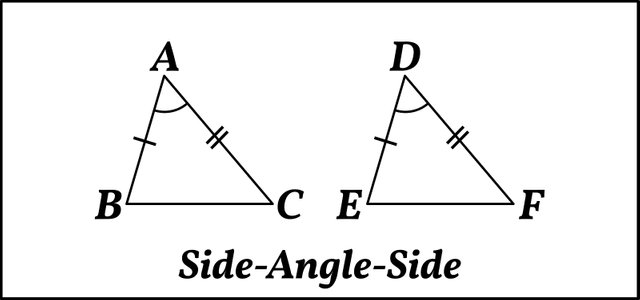
In this argument no appeal is made to any of the postulates nor to the first three propositions ... Nor is there any appeal to the common notions, except perhaps Common Notion 4 (which says that “things which coincide with one another are equal to one another”); and above it was already remarked that there are reasons for thinking Common Notion 4 is an interpolation. Thus from an axiomatic point of view Proposition 4 is based on nothing.
The unsatisfactory nature of Euclid’s proof by superposition of figures is a commonplace, but how this commonplace can be reconciled with the view that Euclid (Book I) had the axiomatic method it is difficult or, rather, impossible to say.
Bertrand Russell (Principles of Mathematics, p. 405) says that Euclid would have done better to assume I, 4 as an axiom. Yes, but Euclid couldn’t have done that, for the simple reason that he had no inkling of a geometric axiom. If our present thesis is correct, Euclid wished to prove everything. (Seidenberg )
Russell’s comments on this point are worth quoting:

390. The fourth proposition is the first in which Euclid employs the method of superposition—a method which, since he will make any détour to avoid it, he evidently dislikes, and rightly, since it has no logical validity, and strikes every intelligent child as a juggle. In the first place, to speak of motion implies that our triangles are not spatial, but material. For a point of space is a position, and can no more change its position than the leopard can change his spots. The motion of a point of space is a phantom directly contradictory to the law of identity: it is the supposition that a given point can be now one point and now another. Hence motion, in the ordinary sense, is only possible to matter, not to space. But in this case superposition proves no geometrical property ...
... 391. Returning now to Euclid’s fourth proposition, we see that the superposition of ABC on DEF involves the following assumptions. (1) On the line DE there is a point E, on either side of D, such that DE = AB. This is provided for by the postulate about the circle. (2) On either side of the ray DE, there is a ray DF such that the angle EDF is equal to the angle BAC. This is required for the possibility of a triangle DEF such as the enunciation demands, but no axiom from which this follows can be found in Euclid. The problem, to construct an angle EDF equal to BAC, does not occur till I. 23, and there I. 4 is used in the proof. Hence the present assumption must be added to Euclid’s axioms. It now follows that on DF there is a point F such that DF = AC. Hence the possibility of two such triangles as the enunciation demands is established. But in order to prove that DEF is equal in all respects to ABC, we need a further axiom, namely: With one angle at D, one side along the ray DE, and the other side of the right (or left) of DE, there exists a triangle which is equal in all respects to the triangle ABC. This is, in fact, the exact assumption which is concealed in the method of superposition. With this assumption, it finally becomes possible to prove that DEF is the triangle satisfying the above conditions and equal in all respects to ABC. (Russell 411 ... 412-413, §§ 390-391)
In his translation of the Elements, Richard Fitzpatrick’s opinion concerning superposition is rather more succinct:
The application of one figure to another should be counted as an additional postulate. (Fitzpatrick 11 fn)

After much discussion on the validity of Euclid’s postulates and common notions, Seidenberg concludes his paper thus:
Our main thesis is that Euclid did not have an axiom system in mind, and did not develop geometry axiomatically, in Book I of The Elements. The main impediment to establishing this thesis is that the Book does have explicitly stated assumptions, indeed, several sets of them: there are the Postulates and the Common Notions ...
If Book I was supposed to have been founded axiomatically, we can only conclude that this was most ineptly done. On the other hand, it is clear that the Book itself is masterfully conceived. The author, beginning with Proposition 1, wastes no words, goes directly to his goal, keeps to essentials, and does not allow himself to get sidetracked. The first 26 propositions give us the basic constructions and basic facts about the mutual relations of the sides and angles of triangles. Then come 7 propositions establishing the theory of parallels, which is needed, first, for the theory of area, and then in Proposition 46 for constructing a square. The author then still adroitly includes the famous Theorem of Pythagoras and its converse. The Book sans Common Notions and Postulate 4 (and the definitions) is worthy of a great mathematician. We see then how unjust it is to attribute an axiomatic method to the author.
Bolyai, writing to his father about his work on the theory of parallels, said: “From nothing I have created another wholly new world.” Euclid might very well have taken this proud declaration as his motto. (Seidenberg )
Bertrand Russell was not willing to go so far as to deny the axiomatic nature of Euclid’s geometry. In his opinion, Euclid’s geometry does constitute an axiomatic system, albeit a flawed one in that several of the essential axioms that underpin it are never stated explicitly in the Elements:
But enough has been said to show that Euclid is not faultless, and that his explicit axioms are very insufficient. (Russell 413)
Russell even accuses Euclid of relying on unstated axioms without being consciously aware of the fact:
The next remark concerns I. 6. Here Euclid first employs an axiom of which he is wholly unconscious, though it is very essential to his system ... (Russell 413)
It is probably fair to say that if Euclid’s geometry constitutes an axiomatic system, then it is a seriously flawed one.

The Mouseion of Alexandria, where Euclid is believed to have taught, was a large centre of learning that later included the famous Library of Alexandria:
Our only knowledge of the ancient Mouseion comes from ancient texts. The ancient texts tell us that the Mouseion was part of the palace complex at Alexandria, which was believed to have been situated along the northeast angle of the promontory of Lochias, which locked in the harbor on the east. (Tour Egypt)
Constructive Geometry
Another term that has been traditionally used to describe Euclid’s geometry is constructive. What this means and how it is relevant to the present discussion will be explored in the next article in this series.
And that’s a good place to stop.
References
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Danielle Macbeth, Diagrammatic Reasoning in Euclid’s Elements, Philosophical Perspectives on Mathematical Practice, College Publications, Rickmansworth, Hertfordshire (2010)
- Glenn R Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- Bertrand Russell, Principles of Mathematics, Routledge, Abingdon, Oxfordshire (2010)
- Abraham Seidenberg: Did Euclid's Elements, Book I, Develop Geometry Axiomatically?, Archive for History of Exact Sciences, Volume 14, Number 4 (30 December 1975), pp 263-295, Springer, New York (1975)
Image Credits
- Aristotle: Lysippos (original sculptor), Museo Nazionale Romano di Palazzo Altemps, Rome, Jastrow (photographer), Public Domain
- Xanthos (Lycia), Childhood Home of Proclus: © Haluk Comertel, Creative Commons License
- Glenn R Morrow: © Rutgers, The State University of New Jersey, Fair Use
- Johan Ludvig Heiberg: Frederik Riise (photographer), Det Kongelige Bibliotek, Copenhagen, Public Domain
- Bertrand Russell: Bertrand Russell in 1907, Public Domain
- Abraham Seidenberg: © George M Bergman (photographer), Creative Commons License
- Plan of Alexandria: William Shepherd, Historical Atlas, pp 34-35, Henry Holt & Co, New York (1911), The University of Texas Libraries, The University of Texas at Austin, Perry-Castañeda Library Map Collection, © Philg88, Creative Commons License
Online Resources
