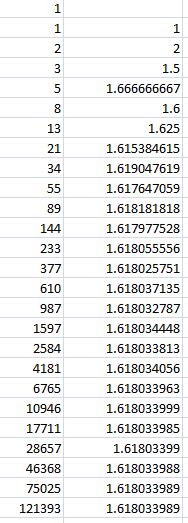
The Fibonacci sequence is a series of numbers where, after two starting values (1 + 1), each following number is the sum of the two proceeding numbers (1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, etc.) Phi = 1.618033988749894848204586834...
(An irrational number that goes on forever without repeating a pattern)
How you begin to get phi through the Fibonacci sequence is by dividing each proceeding number by the last. Example : 1 / 1 = 1, 2 / 1 = 2, 3 / 2 = 1.5, 5 / 3 = 1.6666..., 8 / 5 = 1.6, 13 / 8 = 1.625 and so on
As you can see the further you go the closer the resulting number begins to get closer and closer to phi.
Phi is used in nature, art, architect, etc. because of how irrational (unique) the number truly is. For instance if I'm a flower and I'm trying to grow in a sequence so that each peddle optimizes for getting the most sun light without overlapping other peddles I would grow out my first leaf anywhere, then my second leaf at an angle that is 360° (a circle)/phi (1.618...) This would allow the plant to pop up new leafs in the spaces between old leafs without ever quite filling in evenly, so there's always room for one more leaf without ever having to do a whole new layer. Easiest to see in flowers that spiral like sunflowers 🌻
Another fun fact is some people use Fibonacci as a way to set up bets in gambling to have the best odds of being profitable. To do this, each wager should be the sum of the previous two wagers until a win is made. When you win, the bet goes back two numbers in the sequence because their sum was equal to the previous bet. 😎 Pretty cool I must say!
I wish I could explain the way these numbers effect us and all things around us, but it would cause me to write a book.
If you have more information or thoughts on the topic, please share below in the comment section. Also, like usual, if there's something you would like us to cover next also let us know in the comment section as well.