4-4. Model prediction
Next, the trained model is matched forward. statsmodels provides static and dynamic options for matching and forecasting. The difference lies in whether the observation value is used in the next step of forecasting, or the prediction value generated in the previous step is used iteratively. The prediction effects of log_return (logarithmic rate of return) are as follows:
In [37]:
start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date
pred_dy = model_results.get_prediction(start=start_date, dynamic=False)
pred_dy_ci = pred_dy.conf_int()
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)
plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()
Out[37]:
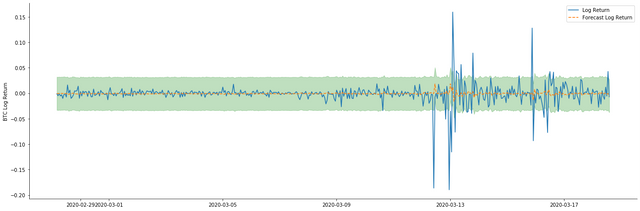
It can be seen that the fitting effect of the static mode on the sample is excellent, the sample data can be almost covered by 95% confidence interval, and the dynamic mode is a little out of control.
So let's look at the data matching effect in dynamic mode:
In [38]:
start_date = '2020-02-28 12:00:00+08:00'
end_date = start_date
pred_dy = model_results.get_prediction(start=start_date, dynamic=True)
pred_dy_ci = pred_dy.conf_int()
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(18, 6))
ax.plot(kline_all['log_return'].loc[start_date:], label='Log Return', linestyle='-')
ax.plot(pred_dy.predicted_mean.loc[start_date:], label='Forecast Log Return', linestyle='--')
ax.fill_between(pred_dy_ci.index,pred_dy_ci.iloc[:, 0],pred_dy_ci.iloc[:, 1], color='g', alpha=.25)
plt.ylabel("BTC Log Return")
plt.legend(loc='best')
plt.tight_layout()
sns.despine()
Out[38]:
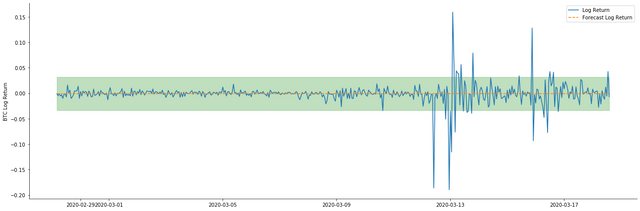
It can be seen that the fitting effect of the two models on the sample is excellent, and the mean value can be almost covered by the 95% confidence interval, but the static model is obviously more suitable. Next, let's look at the prediction effect of 50 steps out-of-sample, that is, the first 50 hours:
In [41]:
# Out-of-sample predicted data predict()
start_date = '2020-03-01 12:00:00+08:00'
end_date = '2020-03-20 23:00:00+08:00'
model = False
predict_step = 50
predicts_ARIMA_normal = model_results.get_prediction(start=start_date, dynamic=model, full_reports=True)
ci_normal = predicts_ARIMA_normal.conf_int().loc[start_date:]
predicts_ARIMA_normal_out = model_results.get_forecast(steps=predict_step, dynamic=model)
ci_normal_out = predicts_ARIMA_normal_out.conf_int().loc[start_date:end_date]
fig, ax = plt.subplots(figsize=(18,8))
kline_test.loc[start_date:end_date, 'log_return'].plot(ax=ax, label='Benchmark Log Return')
predicts_ARIMA_normal.predicted_mean.plot(ax=ax, style='g', label='In Sample Forecast')
ax.fill_between(ci_normal.index, ci_normal.iloc[:,0], ci_normal.iloc[:,1], color='g', alpha=0.1)
predicts_ARIMA_normal_out.predicted_mean.loc[:end_date].plot(ax=ax, style='r--', label='Out of Sample Forecast')
ax.fill_between(ci_normal_out.index, ci_normal_out.iloc[:,0], ci_normal_out.iloc[:,1], color='r', alpha=0.1)
plt.tight_layout()
plt.legend(loc='best')
sns.despine()
Out[41]:
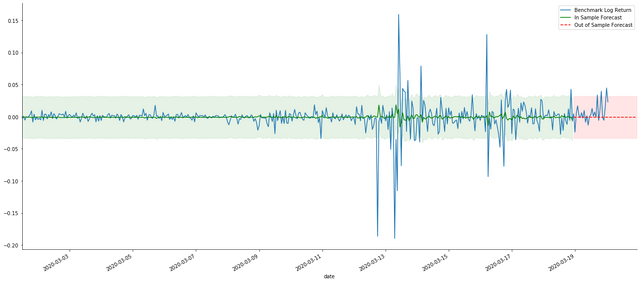
Because the matching of data in the sample is a rolling forward prediction, when the amount of information in the sample is sufficient, the static model is prone to over matching, while the dynamic model lacks reliable dependent variables, and the effect becomes worse and worse after iteration. When forecasting the data outside the sample, the model is equivalent to the dynamic model within the sample, so the accuracy of the error term of long-term prediction is bound to be low.
To be continued...