Inscribed angle of a semicircle always forms a right angle
We want to find the angle AUB (i.e., ∠AUB). Let’s state the conditions imposed on this concept and then see what the implication is for ∠AUB.
Firstly, make a circle C as shown below. Secondly, form a diameter by drawing a line through the center of this circle. The diameter AB is shown. Now, pick any point on the circle (neither inside the circle nor outside) that is different from points A and B; the point U is shown. Next, draw lines (chords) from U to B and from U to A.
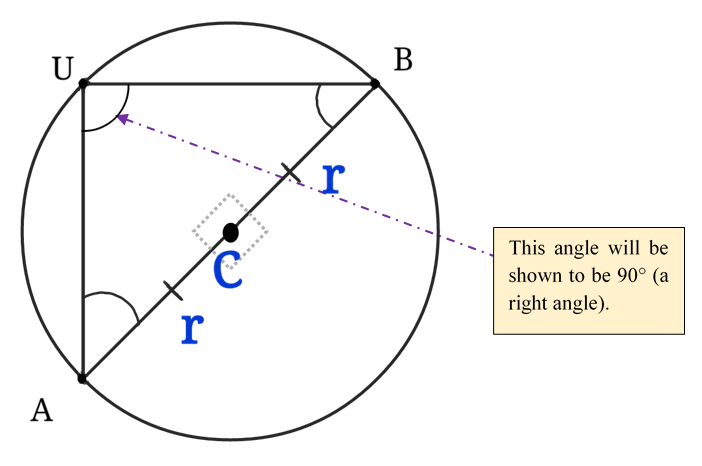
The purpose of this post is to show that whenever lines (chords) are drawn from endpoints of any diameter, the angle formed between those chords is always 90° regardless of where U is on the circle. In other words, ∠AUB is always a right angle (90°) when point U is connected to points A and B. Remember that A and B are endpoints of any diameter of the circle.
The proof of this is rather simple once you accept the fact that the internal angles of a triangle sum to 180° (Euclidean geometry). This fact will be demonstrated in another post. This means that ∠AUB+∠UBA+∠BAU is 180°.
Given:
- AB is a diameter of circle C.
- r is the radius of the circle C.
Known:
- ∠AUB+∠UBC+∠CAU is 180°.
Now draw a radius from C to U (shown next).
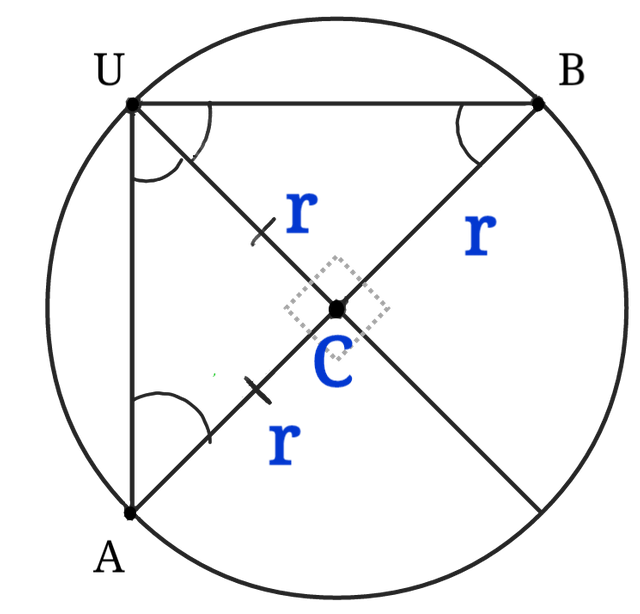
Two isosceles triangles are formed. The triangle CUB is an isosceles triangle as two sides have length r. This means ∠BUC≅∠UBC. The triangle CAU is likewise an isosceles triangle for the same reason. This means ∠UAC≅∠AUC. (≅ means congruent. The congruency symbol is used instead of equals (=) when shapes and sizes are being discussed as opposed to numbers).
Note that ∠AUB≅∠AUC+∠BUC.
Use the fact presented earlier:
∠AUB+∠UBC+∠UAC=180°
∠AUC+∠BUC+∠UBC+∠UAC=180°
Recall:
∠AUC ≅∠UAC
∠BUC ≅∠UBC
Thus,
∠AUC+∠BUC+∠BUC+∠AUC=180°
2∠AUC+2∠BUC=180°
2(∠AUC+∠BUC)=180°
∠AUC+∠BUC=90°
∠AUC+∠BUC=∠AUB=90°
This is what we wanted to show. Therefore, ∠AUB = 90°.