
Task1: Introduction to geometry
Let us explore some history. Originally derived in ancient cultures, geometry is among the first fields of mathematics. All started with pragmatic purposes, like ancient Egypt's earth measurement.
Intesting Inforamtion ( i remeber when the techer said to us this information ) :
"the word ‘geometry’ literally means ‘measuring the earth’ in Greek".
In the school :
we utilized equipment like compasses and rulers to study geometry , these tools helped us comprehend the essentials, they had limits in terms of accuracy and visualization. With intriguing software like GeoGebra, we may examine geometric ideas in a manner that is not only dynamic but also incredibly exact. I was fairly excellent in math, particularly geometry, but I had some difficulty with this project because I learned in French, and in Tunisia, we have a French based school system. So, there were several terms I attempted to translate

Task 2: understanding geometric primitives
Let me demonstrate the basic geometric primitives using GeoGebra:
1.Point: The fundamental element of geometry is represented by the symbol 'dot'. Within the GeoGebra environment, points can be created by selecting the 'Point' option and then clicking on the desired location on the plane. Alternatively, you can create a point that is attached to another object. There are two types of points: one that is free and does not belong to any other object, and one that belongs to an object (for example, a point on a line that moves when the line is moved).
2.Line: The infinite collection of points extends in both directions. In order to create a line in GeoGebra, it is necessary to click on the line icon. .
3.Ray:A ray is characterised by its initial point but lacks a defined terminal point, the process of generating a ray within the Geogebra environment entails the utilisation of the designated ray functionality.
4.Segment: A segment of a line is defined as a portion of said line with two endpoints, in the context of the GeoGebra environment, the creation of a segment is initiated by selecting the Segment command, followed by the placement of the first point, which can be done by clicking anywhere on the interface, this is then followed by the placement of the second point
5.Angle: In the context of GeoGebra, the formation of an angle is achieved through the intersection of three points or two intersecting lines, ro initiate the process, the Angle function must be selected, followed by the input of three points, with the midpoint designated as the vertex, or alternatively, two intersecting lines.
Task 3: Adjacent and Vertical Angles
To demonstrate that adjacent angles sum to 180°:
- Created an initial ray
- Added its supplementary ray
- Created a third ray between them
- Measured the angles to show they sum to 180°
ACD + DCB = 180°
For vertical angles:
- Created two intersecting lines
- Measured the vertical angles
- Demonstrated they remain equal even when moving the lines
AED = BEC
AEC = DEB
AEC + BEC = 180°
AED + DEB = 180°
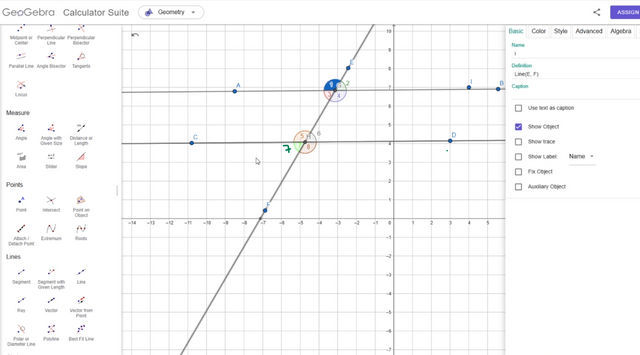
Task 4: parallel and perpendicular lines
Perpendicular (the angels always 90° ) :
Parallel Lines :
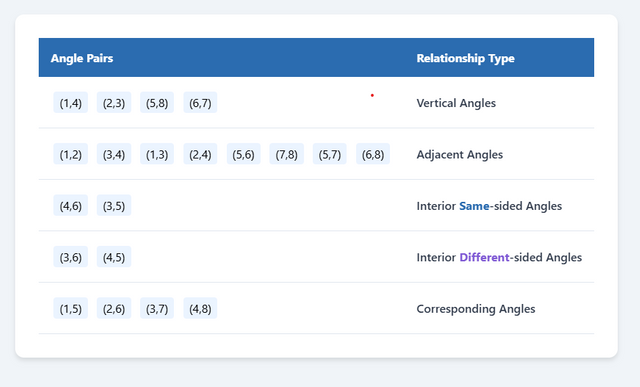
When constructing lines intersected by a transversal, we can identify several angle pairs:
- Corresponding angles (marked in same color)
- Alternate interior angles
- Alternate exterior angles
- Same-side interior angles
- Vertical angles
Task 5: Segment Intersection
To create the intersection point that persists even when segments don't directly intersect:
- Created two segments
- Extended them using the line tool
- Found their intersection point
- Added dashed lines to show the extensions
Working with GeoGebra has made these geometric concepts come alive in ways that traditional tools cannot match. The dynamic nature of the software allows us to see how geometric relationships persist even as we move points and lines around.
I ask my friends @nananrazila, @bimanakhan, and @leonciocastto to join this contest
Hey, I just wanted to let you know that here's the link to my introduction post on Steemit, so you're all set to join me there == > link
About the Author
Hi, I’m Kafio!
- I'm a software engineer interested in data science, trading and development.
- I'm interested in investigating the nexus of technology and innovation, especially data science, trade and software development.
- I'm constantly enthusiastic to learn and share ideas, whether it's studying Computer Science or building new projects.
- I also love to travel
Contact me on [[email protected]] if you have any questions or want to speak.

Upvoted! Thank you for supporting witness @jswit.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit