

OVERVIEW
Getting transactions verified, added to a block and added to the blockchain is not all that easy, especially when you try to do it yourself. Good a thing we have miners and/or validators on the various blockchains.
But how do they manage to verify every single transaction, gather the transactions into blocks, verify and add filled blocks to the blockchain?
One word, hash.

HASH
Hash is simply maths, only that it's not basic maths. Instead, it's a math function that takes a string of data and converts it to another bizarre string of data.
Puzzled? Just wait.
The first string of data, known as the input, can be of any length e.g 'a boy', 'two good boys', 'a good boy is hard to find talk less of two', etc. However, the second string of data is of a fixed length.
E.g
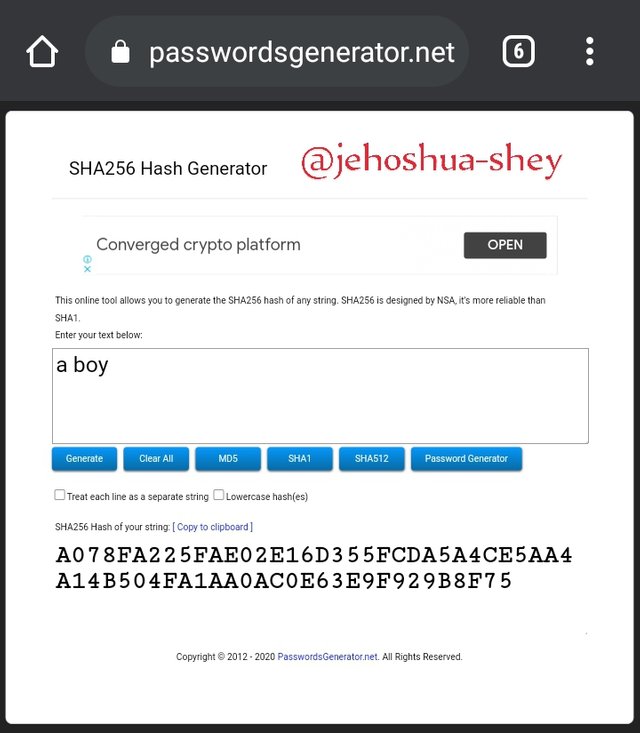
'a boy' would be hashed as 'A078FA225FAE02E16D355FCDA5A4CE5AA4A14B504FA1AA0AC0E63E9F929B8F75'
And
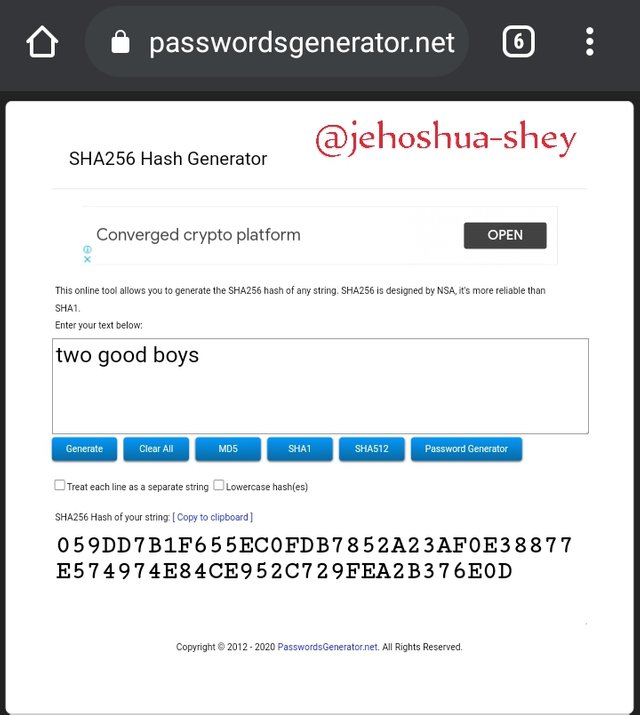
'two good boys' would be hashed as '059DD7B1F655EC0FDB7852A23AF0E38877E574974E84CE952C729FEA2B376E0D'
Now, from the example above, the length of the hash output (called hash value) is the same. That's how hash works.
If you wouldn't mind a gif that gives a more comprehensive illustration
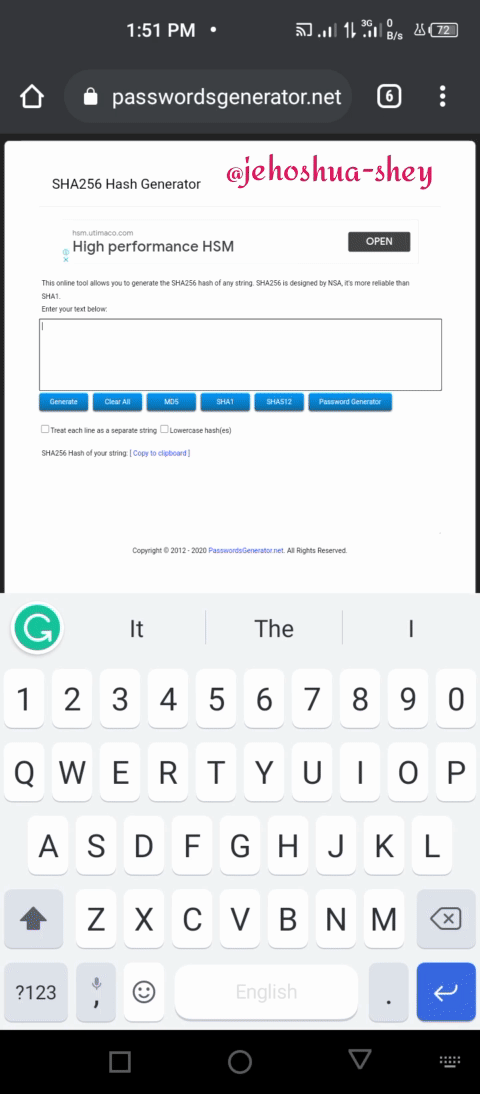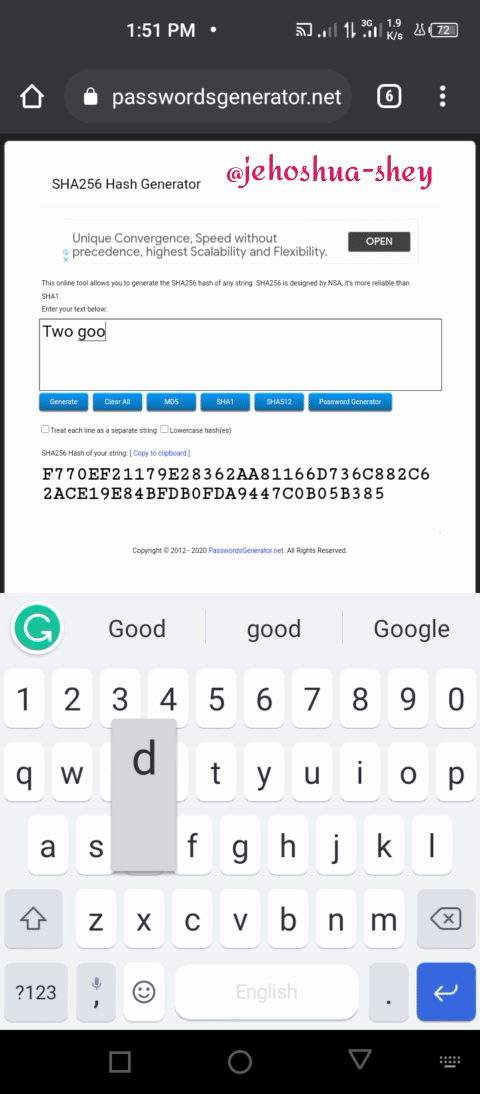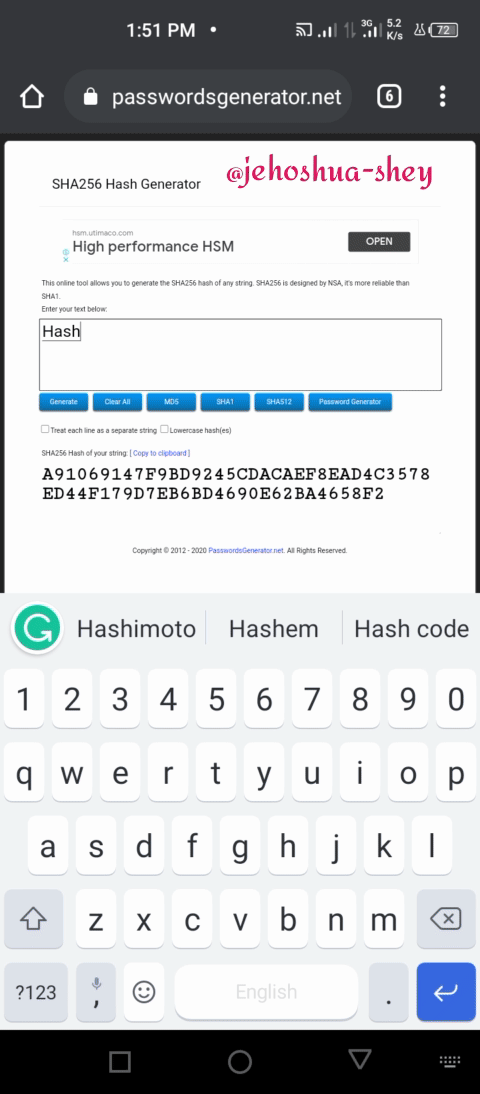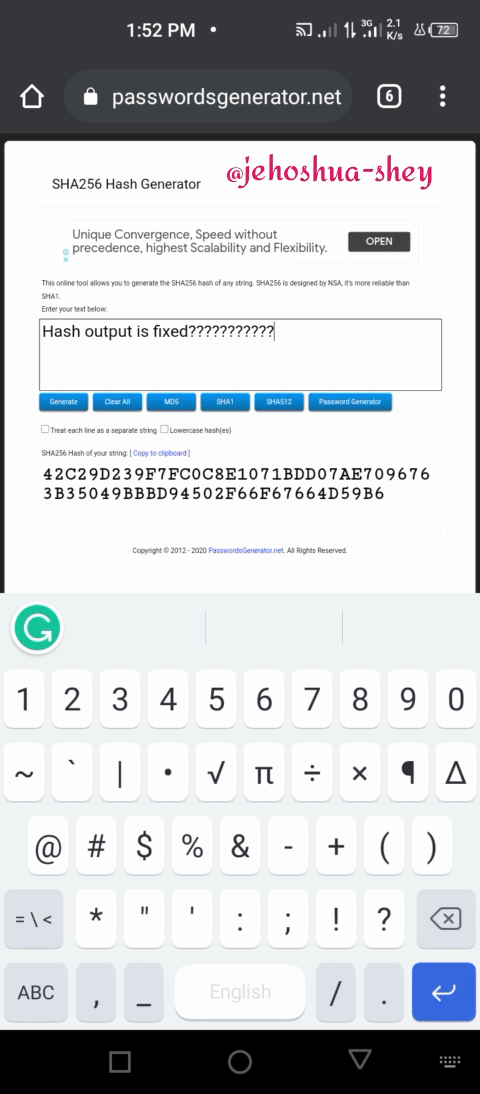
So you now see how that hash outputs don't vary in length right?
Good.
Now, in cryptography, from where we get cryptocurrency, hash (popularly called hash function) was a bit upgraded with some body armour added on. Cryptographers being the nerds they are, spotted some weaknesses in the hash function and decided to tighten up its security.
The 'fork' they did,
And came up with a stealth variant which they christened 'cryptographic hash'. What's new?
No two hash outputs are identical
No reverse engineering (like inputting an output to retrieve its input)
Guessing an input of a cryptographic hash output became as easy as 'successfully mining the remaining bitcoins'. My best wishes when you choose to do so.
With watertight security, cryptographic hash became the go to transaction verification tool in blockchain technology as it could not only hide transaction details, but also could be used to literally summarize any transaction data no matter how lengthy.
Hash output could also be verified. Not by retrieving the input though, but by hashing the exact data claimed to have produced the hash output. This is because the hash output for a given set of data would always be the same.
Now, let's answer an important question.
WHAT IS HASH RATE?
In cryptocurrency mining, hashes are very instrumental in adding a block to the chain. Blockchains that employ PoW require a set of nodes called miner nodes to compete to add each block.
To do this, the miner nodes have to produce a number (which is also a string of data) which when hashed and rehashed with the hash of the block header, will be less than or equal to the target hash.
Please find some friends to have fun with or watch some telemundo, hashing is for miners not you.
If you dare though, this number is called Nonce (Number only used once). It is what determines the hashing difficulty. When it is easier to find, the hashing difficulty is low, when it is not, it means the hashing difficulty is high.
Now, finding this nonce is best done through trial and error. Guided trial and error involving guesses and verification of the guesses.
These guesses are done with complex math computations. The guess is then hashed and rehashed with the block hash and the ensuing hash is compared with the target hash. If it's less than or equal to...boom! Payday!
I talked about hashing difficulty being how easy or not it was to find the nonce. Well, these days, the odds of getting the right nonce at the first guess is beyond gambling.
The norm is, a miner have to guess a string, hash, rehash and compare and then start all over again, hoping that soon enough, the rehash will match.
Interestingly, the computing power the miner has affects how much hash he will be able to do in, say, a second. The more the merrier. The computing power is also identified by the number of hashes it can produce.
Eg. My laptop has a 48 hash per second computing power.
Now, this amount of hash in a given time is what is called HASH RATE.
Hash rates are conventionally in very large measures. Recall that this hash rate is also a measure of computing power, as it tells how much hash the computer processor can deliver in a given time. E.gs of hash rates include
| Hash Rate | Nomenclature | Numerical Rep. (H/s) |
|---|---|---|
| kH/s | kilo hash per second | 1,000 |
| MH/s | mega hash per second | 1,000,000 |
| GH/s | giga hash per second | 1,000,000,000 |
| TH/s | tera hash per second | 1,000,000,000,000 |
| PH/s | peta hash per second | 1,000,000,000,000,000 |
| EH/s | exa hash per second | 1,000,000,000,000,000,000 |
| ZH/s | zeta hash per second | 1,000,000,000,000,000,000,000 |
| YH/s | yotta hash per second | 1,000,000,000,000,000,000,000,000 |
THE IMPORTANCE OF HASH RATE
Majority of the importance of hash rate is appreciated in PoW blockchains like bitcoin. The importance of hash rate includes:
1. Mining
Hash rate determines the possibility of successfully mining a block. Currently the estimated hash rate for mining a bitcoin block is 94.474EH/s according to blockchain.com
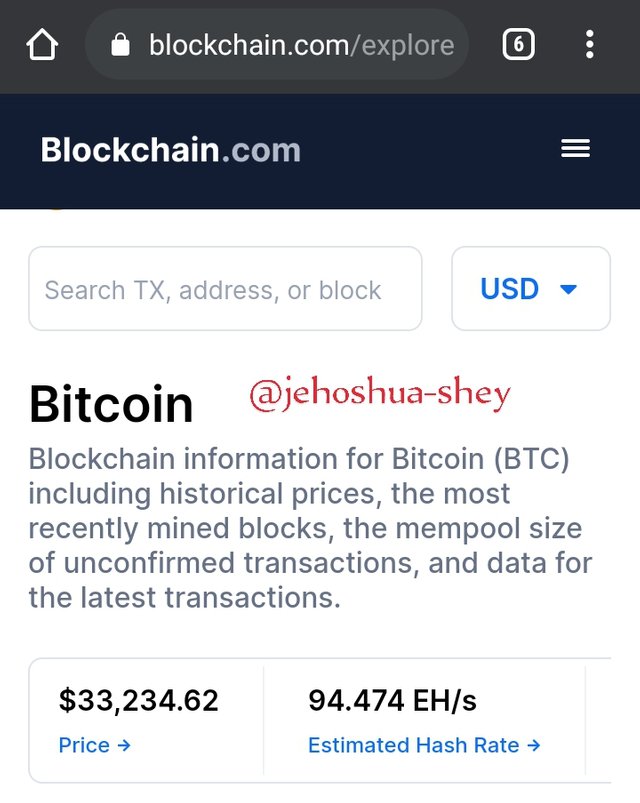
So, to stand a chance to compete, a miner node will have to have a computer power capable of more than 94.473EH/s. Recall, its a race to get the right nonce first. The more the computing power, better the chance of getting the nonce first.
2. Difficulty
Hash rate is what makes mining difficult. When the number of hashes per second required to stand a fair chance of mining is high, it means computing power required is high and unaffordable to miners with less resources. The reverse is also true.
Mining difficulty helps to keep block completion time fixed at approximately 10 minutes.
3. Security
This is another importance of hash rate. As the hash rate rises, it becomes more expensive to carry out an attack on the network as the attacking miner mode will have to have 51% of the total computing power.
Let me take some time to explain this.
Assuming there are 1,000,000 miner nodes each needing about 94.474EH/s, the total hash rate of all miners combined will be
1,000,000 x 94.474EH/s = 94,474,000EH/s = 94.474YH/s
51% of the total hash rate will be
0.51 x 94.474YH/s = 48.18174YH
So the malicious miner node will have to possess computing power of up to 48.18174YH, all the while, hoping that no new miner will join and/or no existing miner will increase their computing power.
The latter is very unlikely. As one miner increases their computing power, they will begin to get the upper hand and the other miners will have to react to remain in business. This means they will also increase their computing power, further increasing the 51% threshold.
There's also the issues then of economic feasibility. Looking at the financial resources required to carry out the attack, how likely will the benefit of the attack cover for it?
THE 51% THRESHOLD
In some blockchains like bitcoin, a miner or set of miners who can control more than 50% (about 51%) of the total computing power in the network can exercise some control over transactions on the network. They could reverse transactions, delay them, double spend, etc.
This is still hypothetical as it has not yet be attempted.
Hash rate and the problem of computational power
The number of hashes a processor can perform in a second determines the chances the miner has to successfully mine a block before others. Explaining this would probably make this post longer but just take it as this,
If the nonce can be gotten within 10 quintillion hashes (10 and eighteen zeros), and a processor can hash 100 quintillion in a second, it means it will take 1/10 seconds to guess 10 quintillion hashes out of which on is the right one.
Such a processor however will require loads of electrical energy to function. It's definitely not your regular CPU. For mining, GPU (graphic processing unit) is preferred. Heavy cooling fans are also involved for favorable weather conditions within and around the computing unit.
Currently, bitcoin uses up more energy than Argentina (121 TWh) and sadly, the miners have chosen to source most of that energy from fossils. That has created all the problems of bitcoin energy consumption as we know it today.
The problem with PoW blockchains like bitcoin which requires extremely high computational power is simply that - the miners have resorted to non-renewable energy sources, thereby polluting the planet.
But can bitcoin be mined with renewable energy sources? Yes.
Will it be economically feasible? Let's do the maths.
Here's a low down on the prices of renewable energy according to forbes
| Renewable source | Cost ($) |
|---|---|
| Onshore wind | 0.1/kWh |
| Solar | 0.1/kWh |
| Geothermal | 0.1/kWh |
| Biomass | 0.1/kWh |
| Hydro | 0.05/kWh |
| Offshore wind | 0.13/kWh |
Now,
Bitcoin requires about 121.36TWh annually, according to BBC
1 Terra Watt = 1,000,000,000 kilo Watts
121.36 Terra Watt = 121,360,000,000 kilo Watts
Multiply that by the cost of 1kWh for hydro($0.05)
That gives $6 billion annually.
See, BTC revenue
6.125 BTC / 10 minutes, with BTC @$33k gives $202k every 10 minutes
A day is ((24 x 60) / 10) x $202k = $29m
A year is 365 x $29m = $10.6 billion
That's $42.4 billion for the entire duration of the 6.125 block rewards.
Mind you, it's at a BTC low price of $33k for $40k, the figures would be $12.8 billion anually
That's about twice the cost of renewable energy plants.
Investing a fraction of this annual BTC fortune in renewable energy will not only power bitcoin, but set up energy distributing multinationals which can be another very lucrative business venture on its own.
Did I mention that some miners also use their mining equipment to mine multiple cryptocurrencies?
Well then, there you go.
So, the problem of hash rate and computational power as we know it, is humans not maths.

MERKLE TREE
Merkle tree is a hash structure that combines hashes to form a hash and continues until a given set of hashes have all be combined into one final hash called the root hash.
Here is a detailed illustration of how it is done.
The leaves provided are:
Steem1, Steem2, Steem3, Steem4, Steem5, Steem6, Steem7, and Steem8.
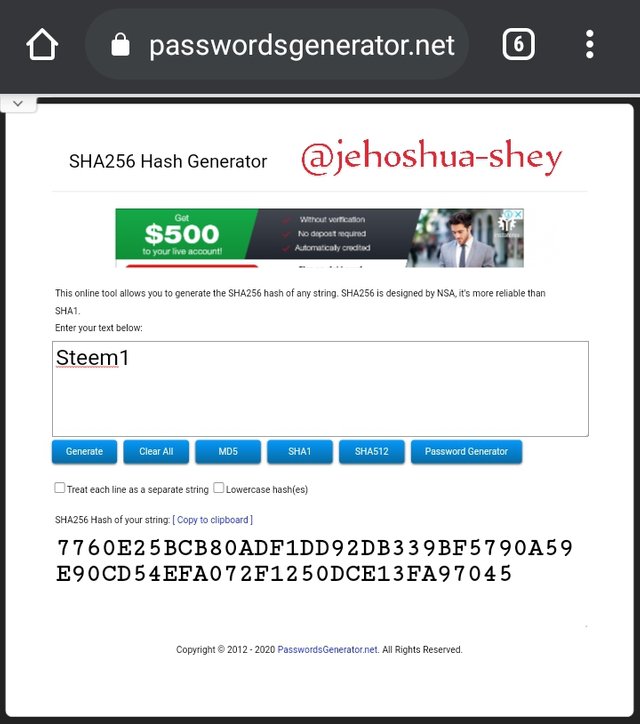
Hashing 'Steem1' gives
7760E25BCB80ADF1DD92DB339BF5790A59E90CD54EFA072F1250DCE13FA97045
Hashing 'Steem2' gives
FE00506E91CF52BC4B35321E6B978D1A7349397B19C6C1C01E095971FDEC9741
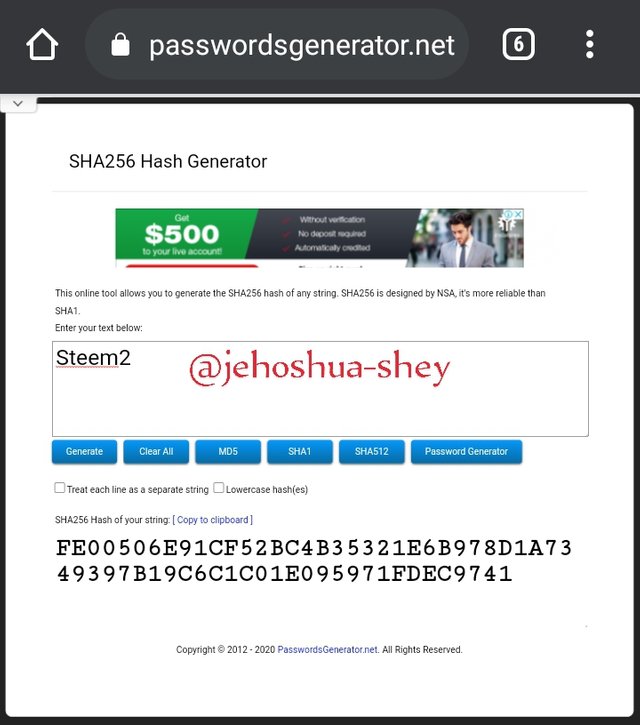
Hashing 'Steem3' gives
A9418332E0C351D6A50C835AA9E57D514F0573C231D491E97726DB8A5844F2DC
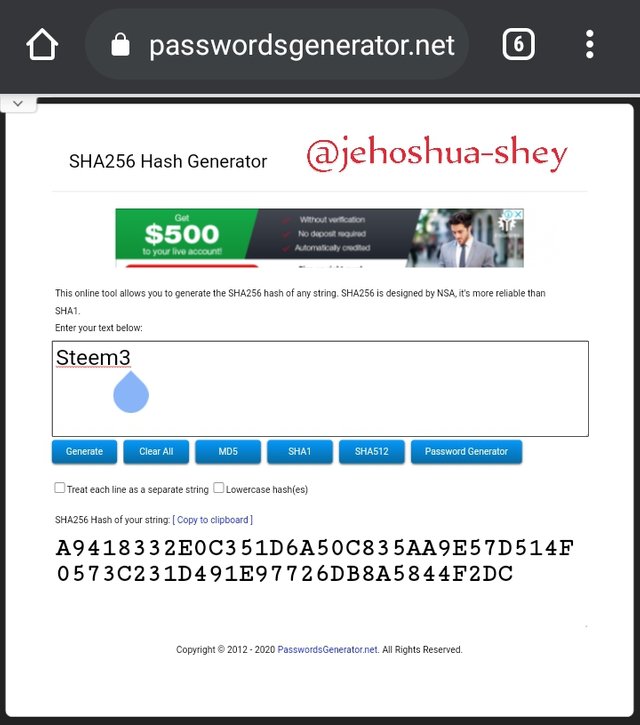
Hashing 'Steem4' gives
22F4EC8E20C9CCAF2C313B23F18981B1C73BF39081BCD739E5D998A95A46AB30
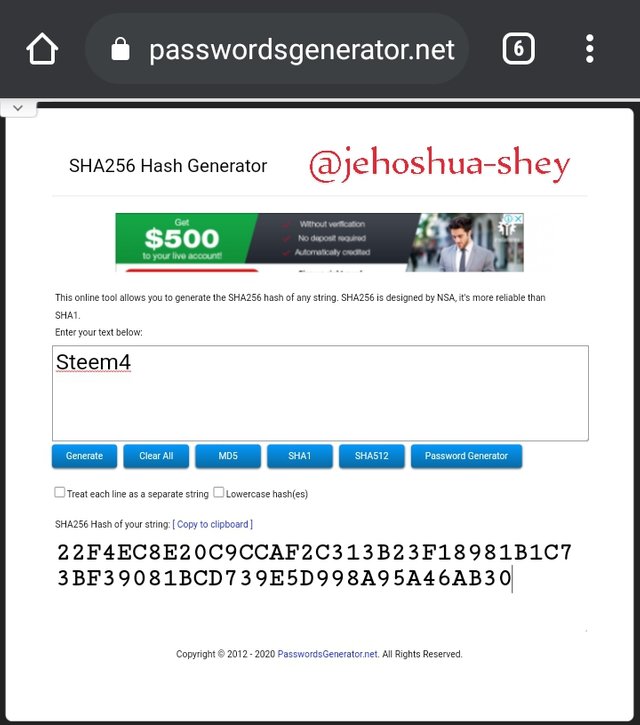
Hashing 'Steem5' gives
2A3C87336683AB0DDFA56AFEFC740E6C13A02FEA0A43D6797343B26D7AF0C57B
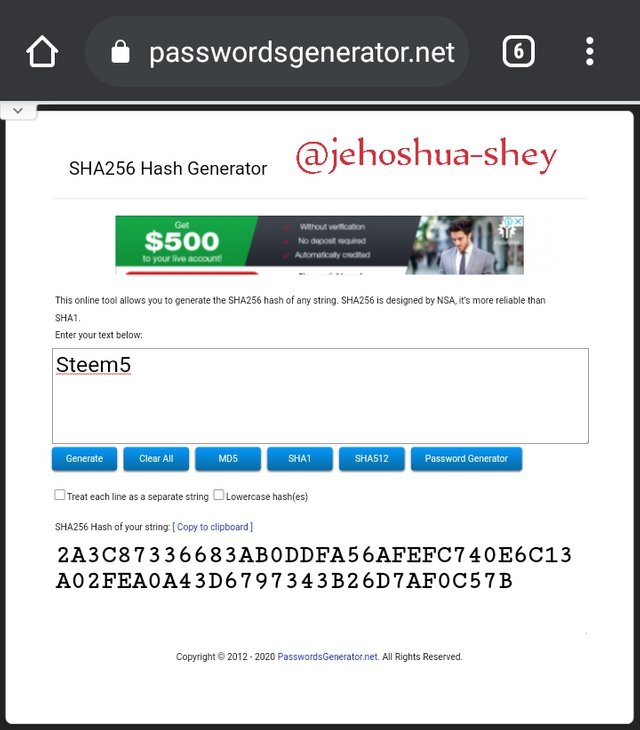
Hashing 'Steem6' gives
A7BAA6DE0C0658E9E3681966E542BACD116529F5AE9A2D9126CDB1C1D5BC1278
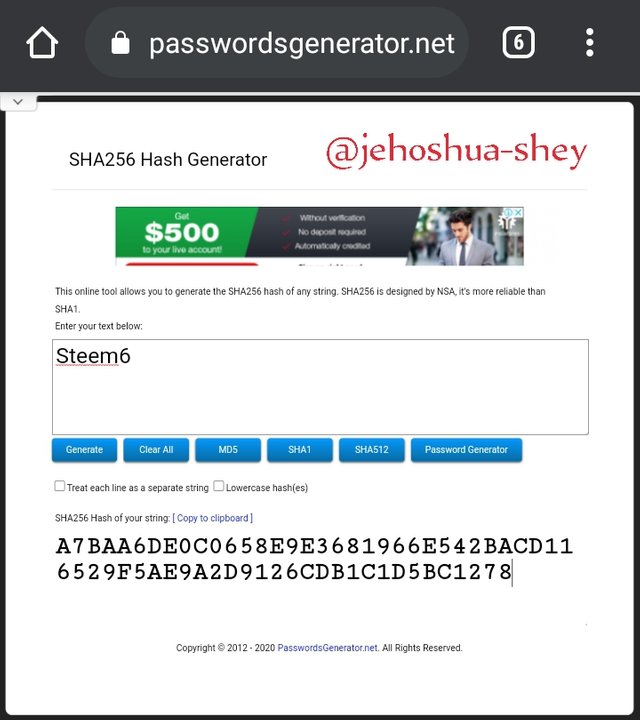
Hashing 'Steem7' gives
D441688DDA7F9285E8811728DD9A3955CF74F0A3C7600C1589D0F1D3B48FFAC7
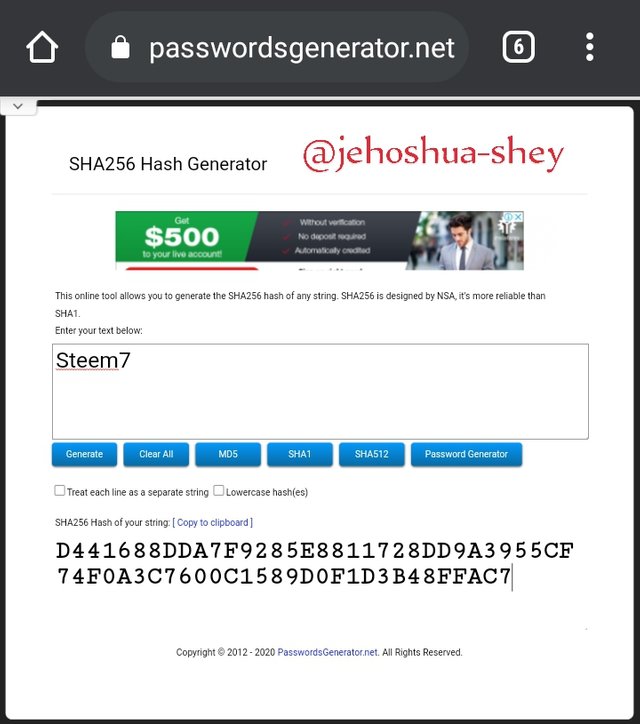
Hashing 'Steem8' gives
F2E38ED4FF662087B6E9BEAFA4158EBC488B995732057BDA019A6A77FFB5F9F5
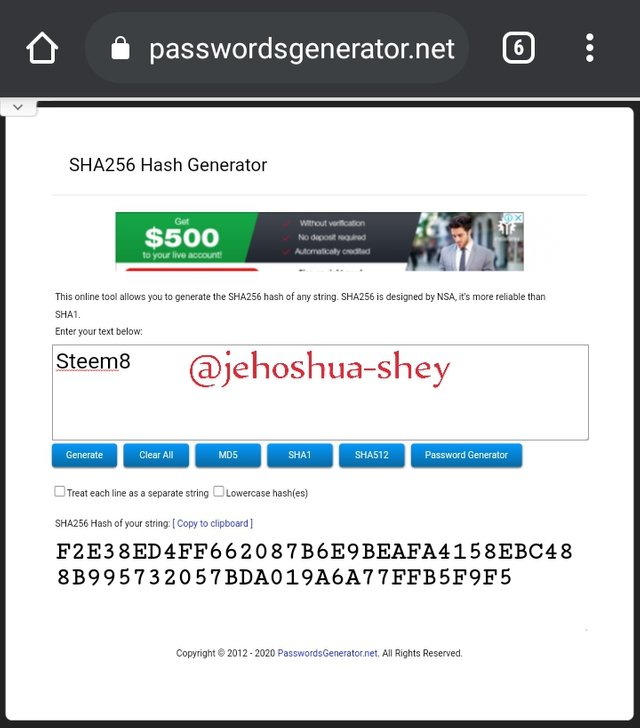
Next, we combine leaves and rehash.
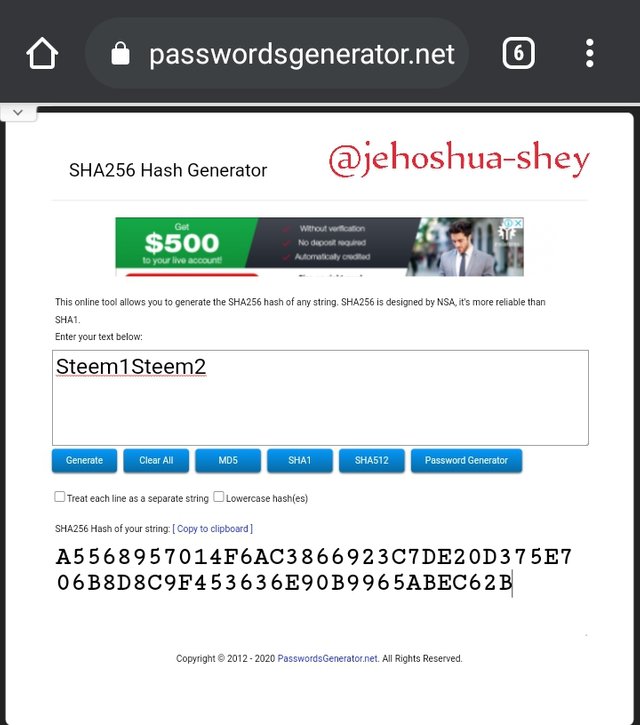
Hashing 'Steem1Steem2' gives
A5568957014F6AC3866923C7DE20D375E706B8D8C9F453636E90B9965ABEC62B
Hashing 'Steem3Steem4' gives
18D25196DB699F6AB9222B7302EB8A6F6EBFADEC703C07DD5DB8D9455913A499
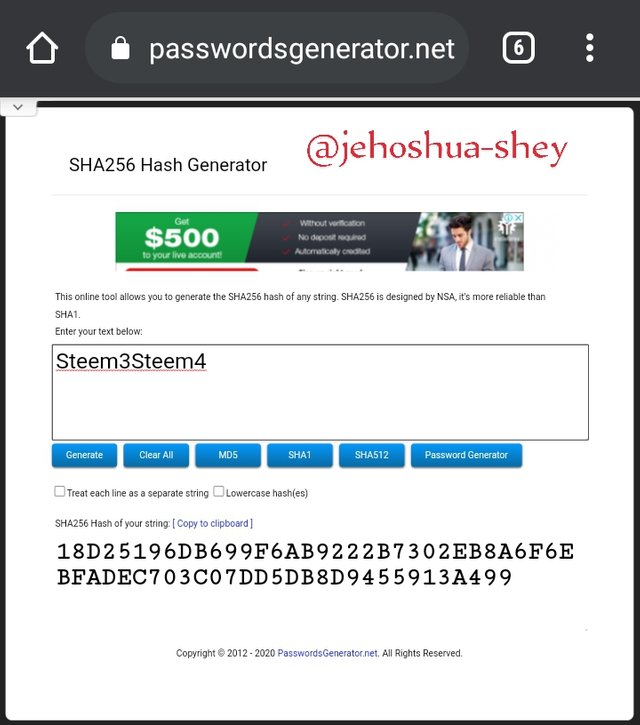
Hashing 'Steem5Steem6' gives
D118E137F92A0DBEA138B6BF70C7714153A7BC393CD0272A44BD94864645224B
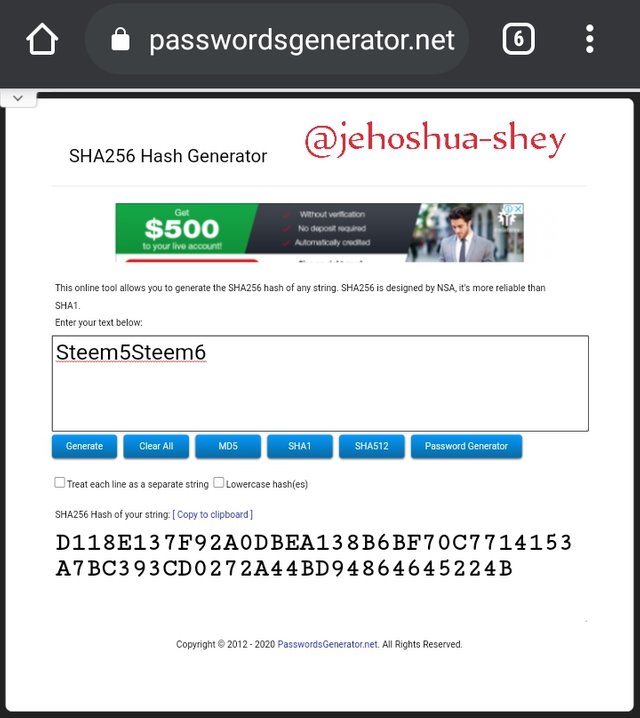
Hashing 'Steem7Steem8' gives
A81D57BA11AEDFA9EFBBA42F6523D75D1EFA50B22C5E3557A21CEFFE87DDFC4A
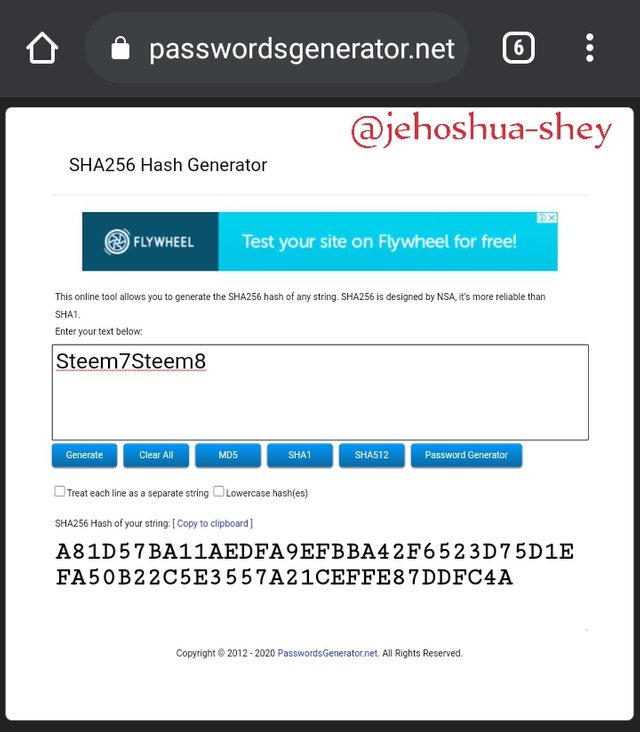
Now, we combine further the rehashed leaves and rehash.
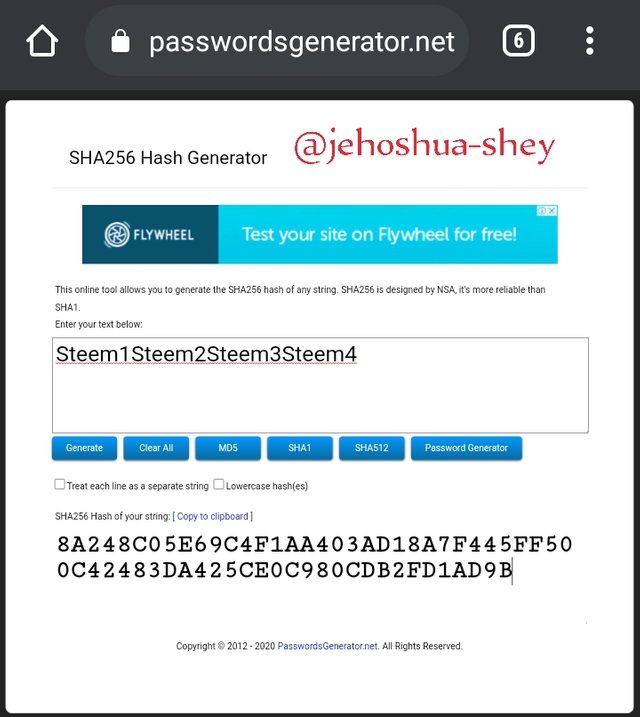
Hashing 'Steem1Steem2Steem3Steem4' gives
8A248C05E69C4F1AA403AD18A7F445FF500C42483DA425CE0C980CDB2FD1AD9B
Hashing 'Steem5Steem6Steem7Steem8' gives
8B0935AEAB3F51BFA2B0750703EE2387E2B20EB19B0D24227E180C03A851AF17
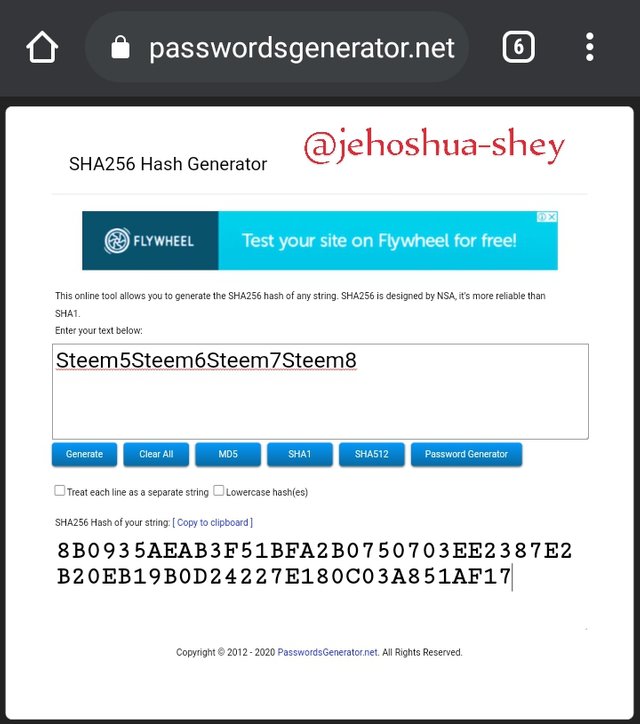
Finally, we combine the last two strings of data and rehash them.
Hashing 'Steem1Steem2Steem3Steem4Steem5Steem6Steem7Steem8' gives
9C2FC83F36D59B8ED5033D2BCC417728583C8DAA0AA9868FD374BE3619D6E4F9
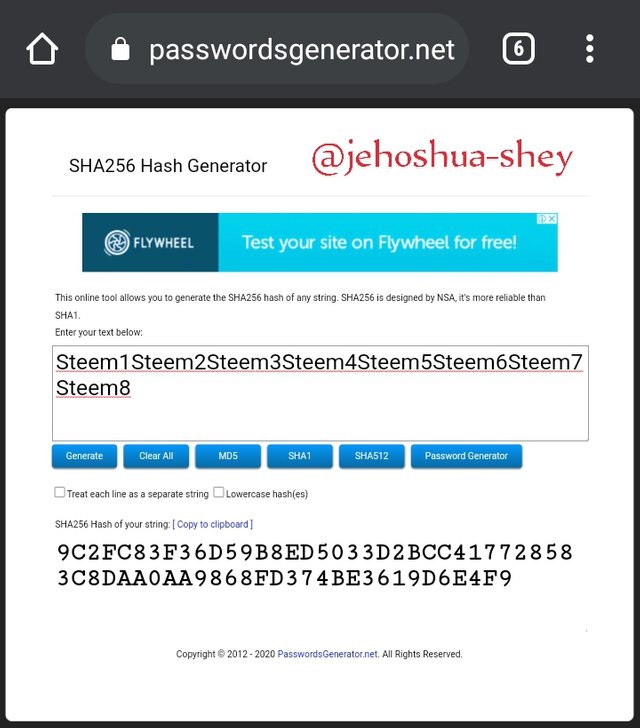
Here's what the merkle tree looks like
CHECKING OUR MERKLE IF IT CONTAINS Steem6
We want to run a check on our merkle tree to see if Steem6 is included in the leaves.
We know that our root hash is
Steem1Steem2Steem3Steem4Steem5Steem6Steem7Steem8
Now we need to go down to the first branch from the root.
At the first branch from the root, we find two siblings
Steem1Steem2Steem3Steem4 and Steem5Steem6Steem7Steem8
Were are searching for Steem6 but we'll move arbitrarily to the left and on the left sibling, we go down to the second branch from the root hash. There we find two siblings
Steem1Steem2 and Steem3Steem4
We move arbitrarily again to the left and go further down to the leaves and we find
Steem1 and Steem2
They are not what we're looking for but at least, we know they are there. Now, we go back up to the second branch from the root and then go RIGHT. At the right sibling (Steem3Steem4), we then go down
There we find two leaves
Steem3 and Steem4
Fine but not our target. We go back all the way up to the first branch from the root. Then we continue in our newly adopted right turn. This is because we've already gone left.
Now, at the right sibling (Steem5Steem6Steem7Steem8) we go down to the second branch from the root and there we find two siblings
Steem5Steem6 and Steem7Steem8
We are in unfamiliar territories so we start with left. From the left sibling, we go down to the leaves and find
Steem5 and Steem6
If you know what we are looking for, you'll know we've found it.
Yes, at the left sibling, we have our Steem6. So, we've been able to trace it on the merkle tree from the root hash.

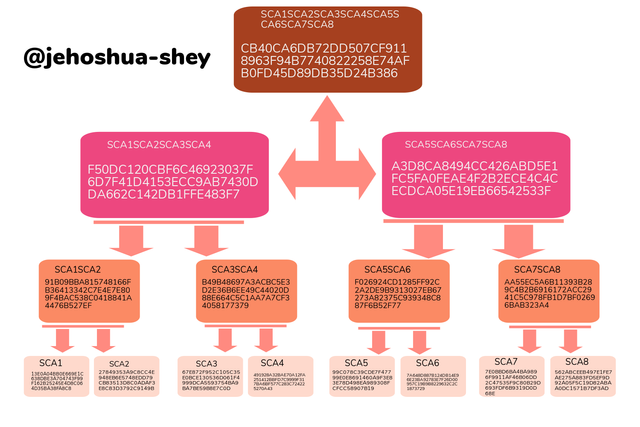
CREATING ANOTHER MERKLE TREE
The leaves provided are:
SCA1, SCA2, SCA3, SCA4, SCA5, SCA6, SCA7, and SCA8.
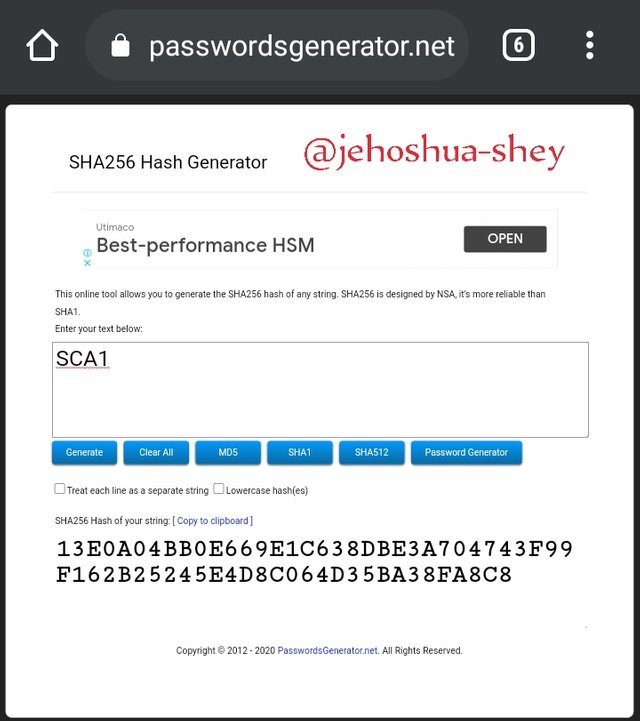
Hashing 'SCA1' gives
13E0A04BB0E669E1C638DBE3A704743F99F162B25245E4D8C064D35BA38FA8C8
Hashing 'SCA2' gives
27849353A9C8CC4E948EB6E5748EDD79CB83513D8C0ADAF3E8C83D3792C9149B
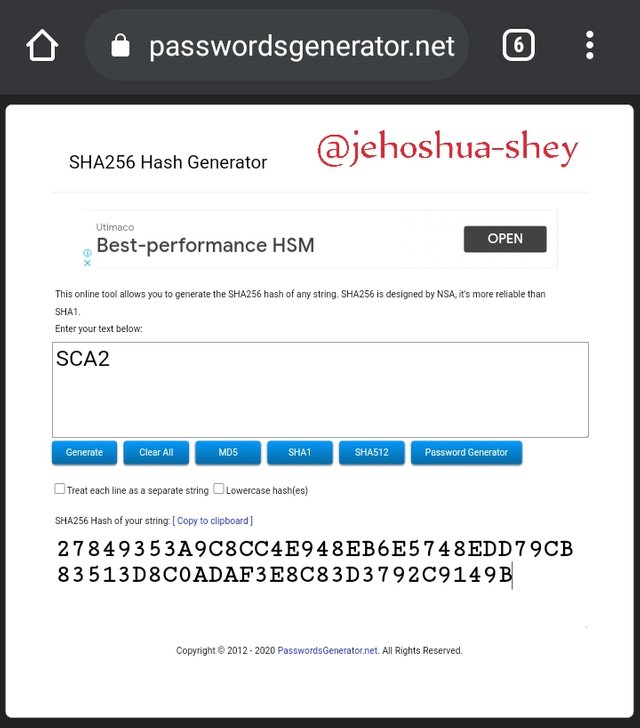
Hashing 'SCA3' gives
67E872F952C105C35E0BCE130536D061F4999DCA5593754BA9BA7BE59B8E7C0D
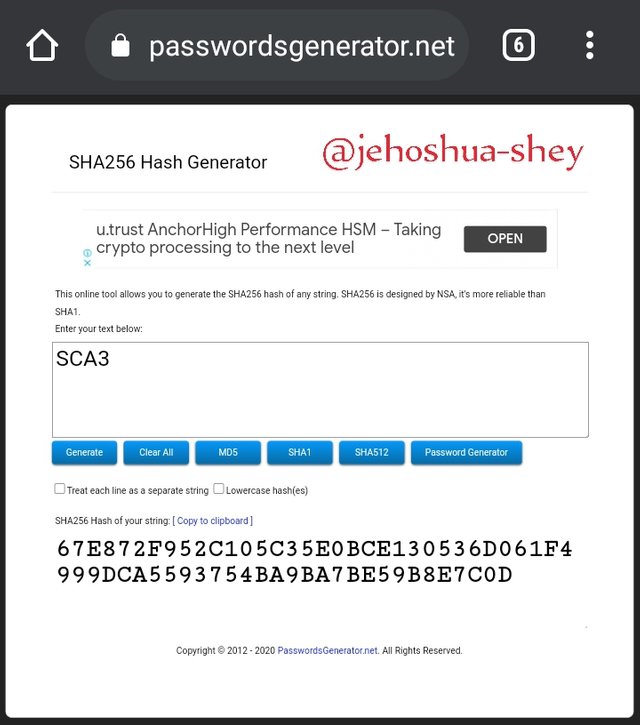
Hashing 'SCA4' gives
491928A32BAE70A12FA251412BBFD7C9999F317BA6BF577C283C724225270A43
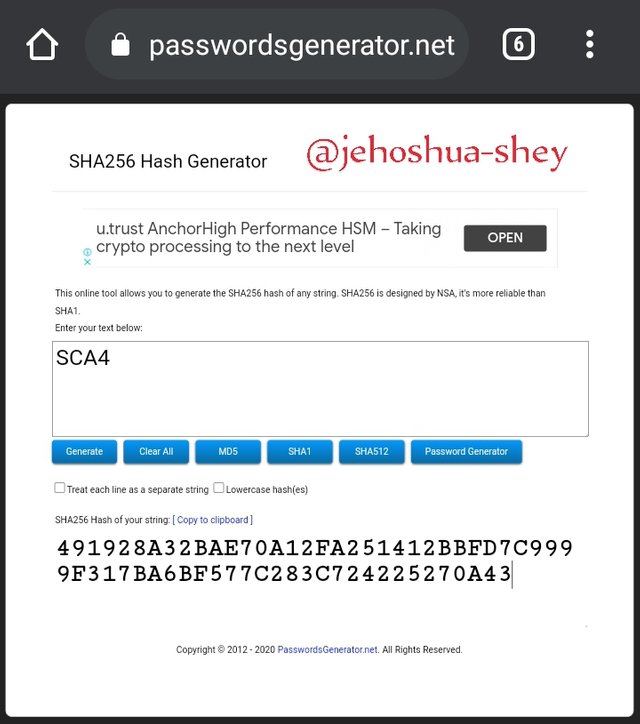
Hashing 'SCA5' gives
99C078C39CDE7F47799E0E8691460A9F3E83E78D498EA989308FCFCC58907B19
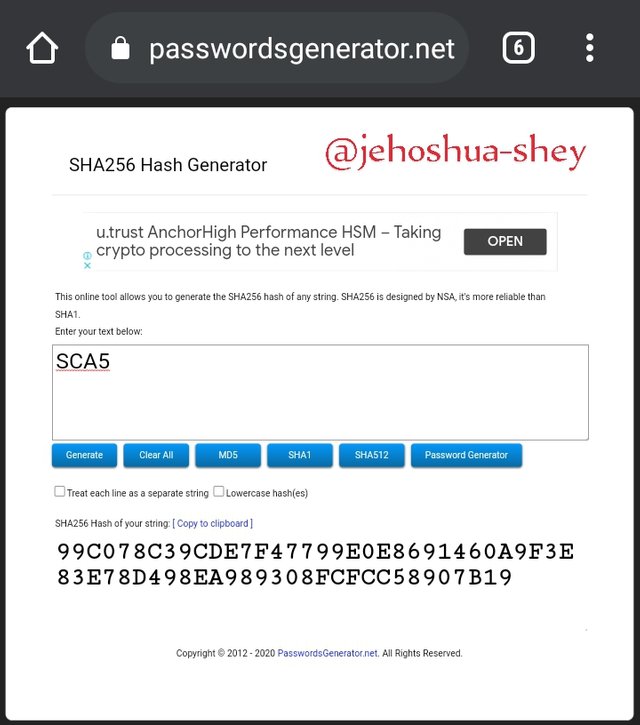
Hashing 'SCA6' gives
7A648D887B124DB14E96E23BA92783E7F26D00957C19B9B8229632C2C1873729
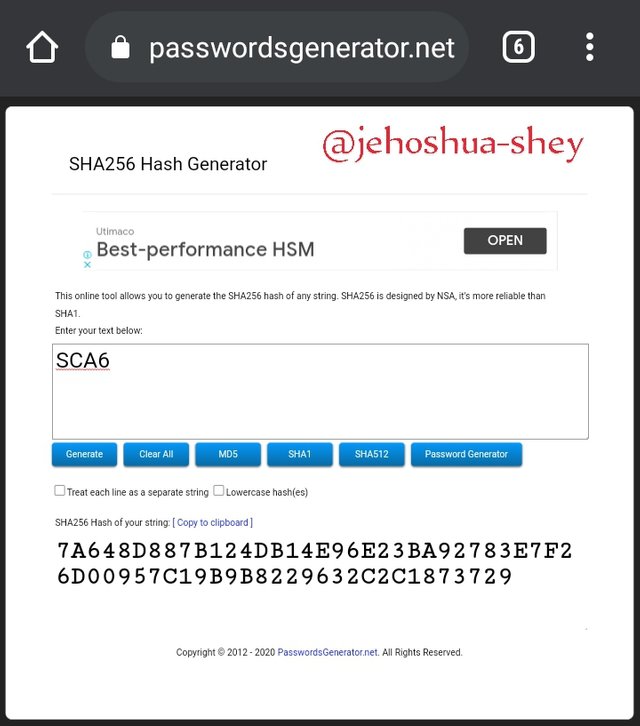
Hashing 'SCA7' gives
7E0BBD6BA4BA9896F9911AF46B06DD2C47535F9C80B29D693FDF6B9319D0D68E
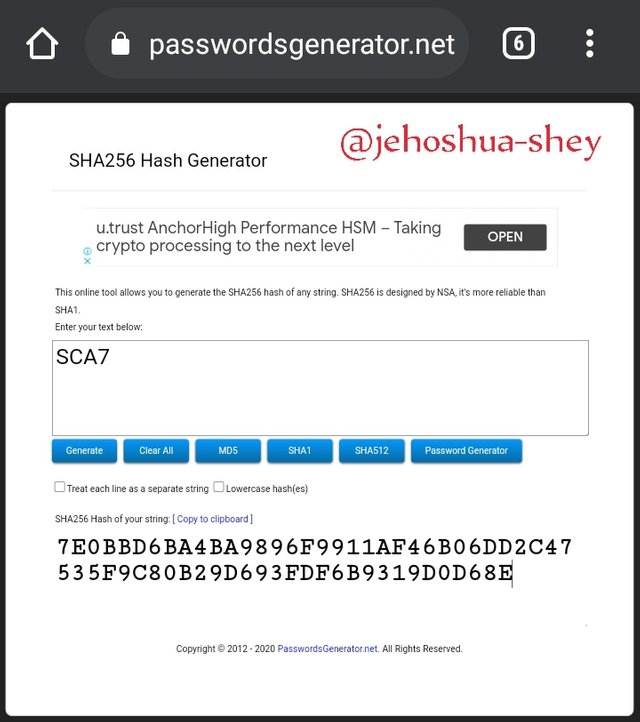
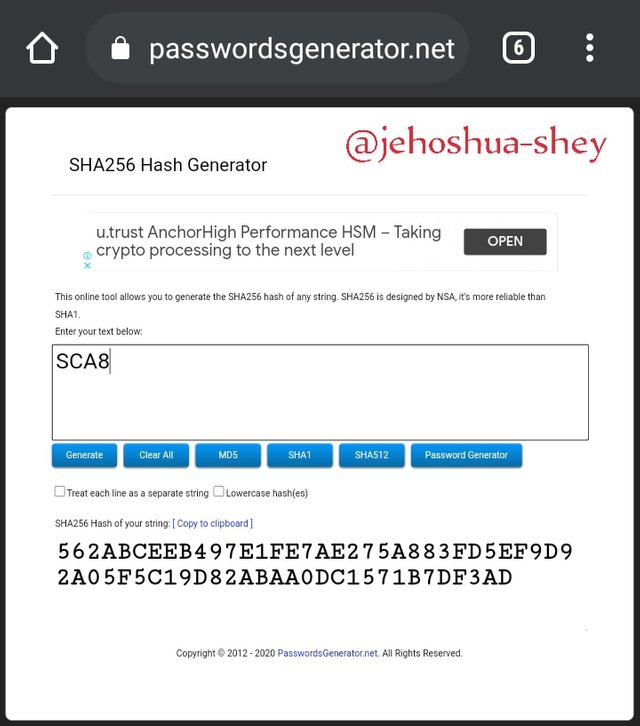
Hashing 'SCA8' gives
562ABCEEB497E1FE7AE275A883FD5EF9D92A05F5C19D82ABAA0DC1571B7DF3AD
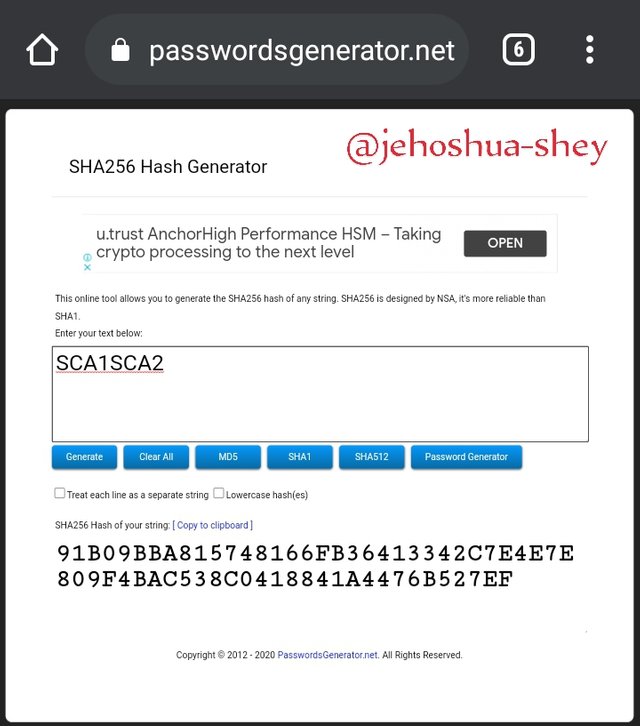
Next, we combine leaves and rehash.
Hashing 'SCA1SCA2' gives
91B09BBA815748166FB36413342C7E4E7E809F4BAC538C0418841A4476B527EF
Hashing 'SCA3SCA4' gives
B49B48697A3ACBC5E3D2E36B6EE49C44020D88E664C5C1AA7A7CF34058177379
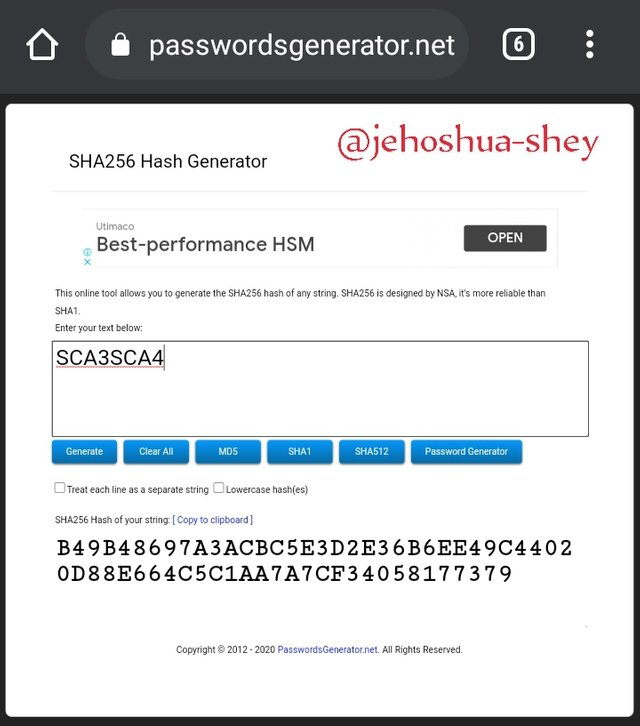
Hashing 'SCA5SCA6' gives
F026924CD1285FF92C2A2DE9B9313027EB67273A82375C939348C887F6B52F77

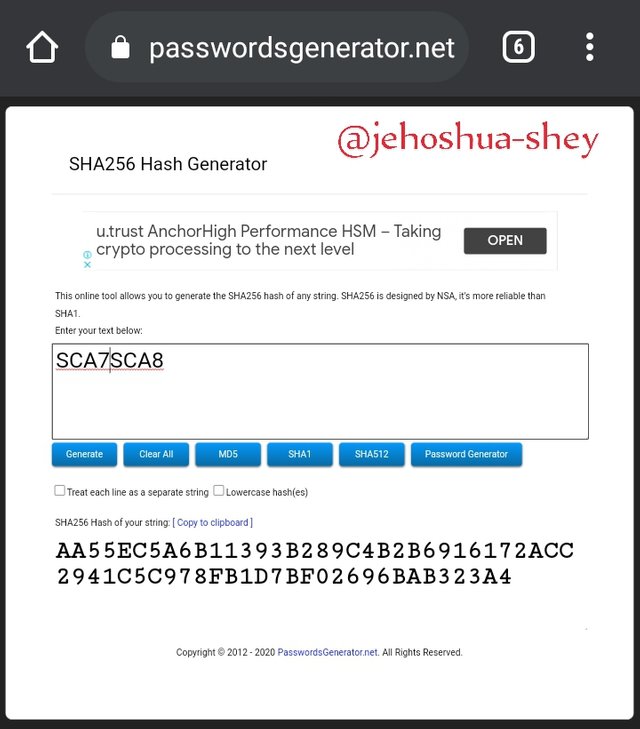
Hashing 'SCA7SCA8' gives
AA55EC5A6B11393B289C4B2B6916172ACC2941C5C978FB1D7BF02696BAB323A4
Now, we combine further the rehashed leaves and rehash.
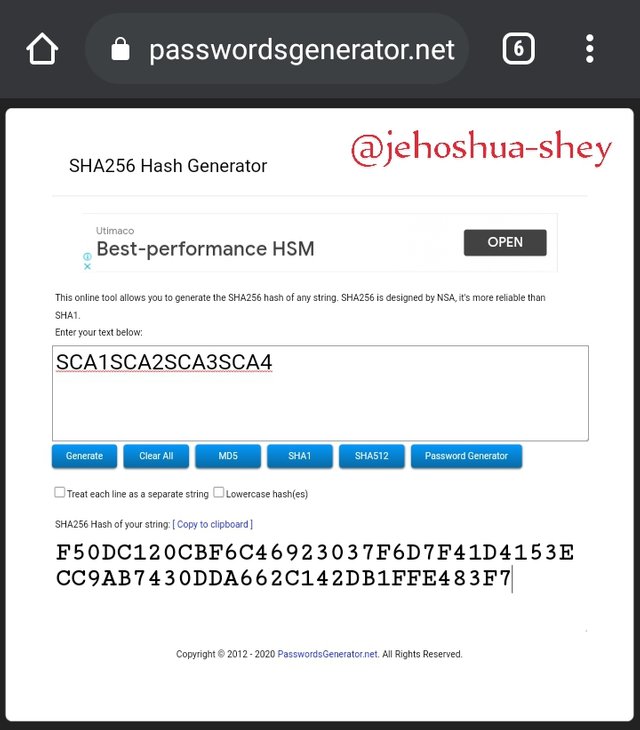
Hashing 'SCA1SCA2SCA3SCA4' gives
F50DC120CBF6C46923037F6D7F41D4153ECC9AB7430DDA662C142DB1FFE483F7
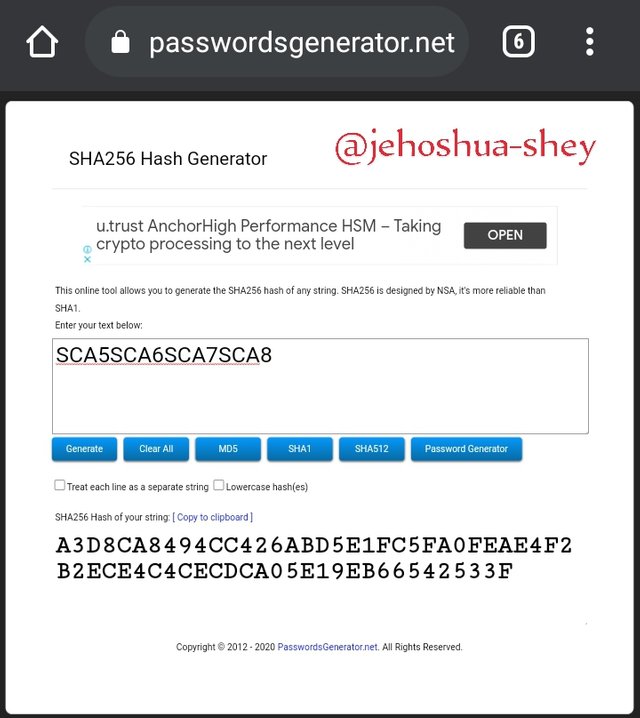
Hashing 'SCA5SCA6SCA7SCA8' gives
A3D8CA8494CC426ABD5E1FC5FA0FEAE4F2B2ECE4C4CECDCA05E19EB66542533F
Finally, we combine the last two strings of data and rehash them.
Hashing 'SCA1SCA2SCA3SCA4SCA5SCA6SCA7SCA8' gives
CB40CA6DB72DD507CF9118963F94B7740822258E74AFB0FD45D89DB35D24B386
Here's what the merkle tree looks like
WHAT TO DO IF THE NUMBER OF LEAVES IS ODD
When dealing with an odd number of leaves, the solution is to concatenate the leaf that has no pair with itself.
E.g. We have leaves A, B, C, D, E, F, G, H, and J
We combine them in pairs to give
AB, CD, EF, GH, then it remains J. J pairs with itself to give JJ
Now for the next branch, we have odd number again and so we repeat the last one which will give
ABCD, EFGH, then it remains JJ, JJ pairs with itself to give JJJJ
In the next branch, we also have odd numbers. The last one keeps pairing with itself whenever there's an odd number of leaves
ABCDEFGH, then JJJJ, JJJJ pairs with itself to give JJJJJJJJ.
The root hash will then be ABCDEFGHJJJJJJJJ.

CONCLUSION
Hashing in cryptocurrency helps secure the blockchains against fraudlent and malicious attacks. PoW blockchains like bitcoin also benefit from the intensive power consumption required for hashing as it renders the economic viablity of attacks null.
Merkle tree is a very important structure in hashing, helping to arrange the data into an easy to understand tree. Beginning with the leaves and hashed up to the root hash, this structure arranges the various hashes into a well organised tree format. It becomes easier to deal with the hashes, either for validation or otherwise.
Thanks for reading.
Cc:
@pelon53
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit