
As we all know PyTorch becomes the most famous platform for Machine Learning and Deep Learning nowadays. Therefore here I try to clear some basic but very useful concepts related to tensors and how it is stored in memory. Without much information let’s start our journey with PyTorch. You can find the following functions in my notebook: tensor-operation.
First thing first:
import torchFunction 1 — torch.storage()
A torch.Storage is a contiguous, one-dimensional array of a single data type.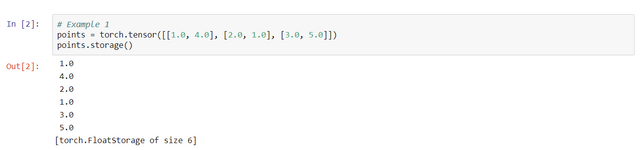
As shown in the example, Even though the tensor reports itself as having three rows and two columns, the storage under the hood is a contiguous array of size 6. In this sense, the tensor knows how to translate a pair of indices into a location in the storage.
You can’t index the storage of a 2D tensor by using two indices. The layout of storage is always one-dimensional, irrespective of the dimensionality of any tensors that may refer to it. 
As we have seen in the above example we can also change the value directly at the storage level by indexing the element.
Function 2 — torch.stride()
To index into storage, tensors rely on a few pieces of information that, together with their storage, unequivocally define them: size, storage offset, and stride.
The size (or shape, in NumPy parlance) is a tuple indicating how many elements across each dimension the tensor represents. The storage offset is the index in the storage that corresponds to the first element in the tensor. The stride is the number of elements in the storage that need to be skipped to obtain the next element along each dimension.
Strides are a list of integers: the k-th stride represents the jump in the memory necessary to go from one element to the next one in the k-th dimension of the Tensor. Here the second point has elements [2.0, 1.0] which are 2 elements far from the first element, so the above example gives us the answer 2.
Here the second point has elements [2.0, 1.0] which are 2 elements far from the first element, so the above example gives us the answer 2. 
We can understand (2, 1) in lemon words: for getting specific elements in memory we have to jump 2 steps in memory per each row and 1 step per each column. Suppose if we want to access 5.0 in memory and currently at we starting point 1.0 then we have to jump 4 steps as the element is on the 2-nd row from current row and 1 steps extra for go to next column, means total steps is 4 + 1 = 5. Therefor to access 5.0 from the current position we have to jump off 5 steps in memory.
Function 3 — torch.clone()
Changing the subtensor has a side effect on the original tensor too: This effect may not always be desirable, so you can eventually clone the subtensor into a new tensor:
This effect may not always be desirable, so you can eventually clone the subtensor into a new tensor:
Function 4 — torch.transpose()
Transposing in PyTorch isn’t limited to matrices. You can transpose a multidimensional array by specifying the two dimensions along which transposing (such as flipping shape and stride) should occur: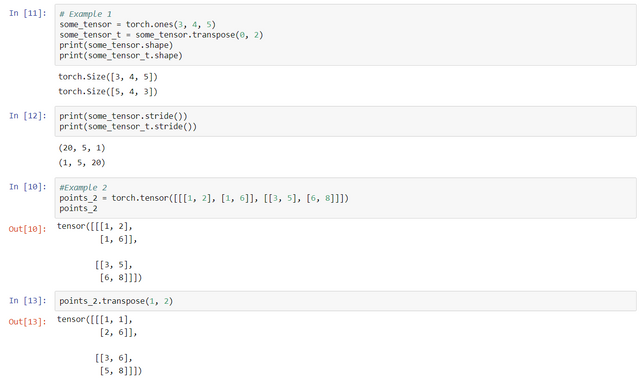
Function 5 — torch.contiguous()
A tensor whose values are laid out in the storage starting from the rightmost dimension onward (moving along rows for a 2D tensor, for example) is defined as being contiguous. Contiguous tensors are convenient because you can visit them efficiently and in order without jumping around in the storage. (Improving data locality improves performance because of the way memory access works in modern CPUs.)
In this case, points are contiguous but its transpose is not: You can obtain a new contiguous tensor from a noncontiguous one by using the contiguous method. The content of the tensor stays the same, but the stride changes, as does the storage:
You can obtain a new contiguous tensor from a noncontiguous one by using the contiguous method. The content of the tensor stays the same, but the stride changes, as does the storage: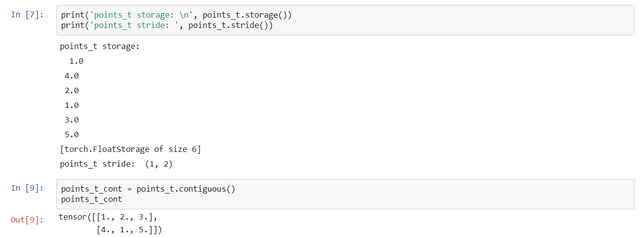
As we can see, .contiguous() function did not affect the view of the tensor, but it actually makes the storage of the tensor in a contiguous manner. 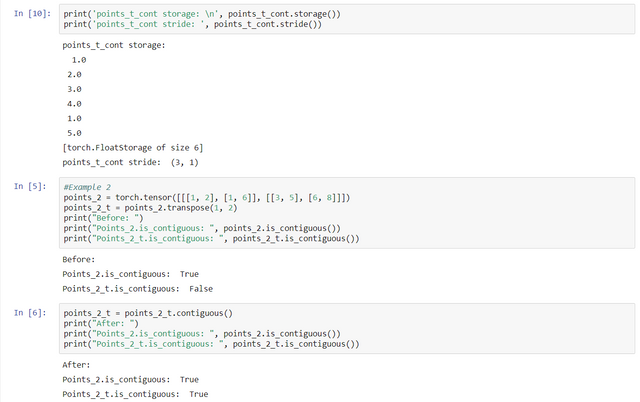
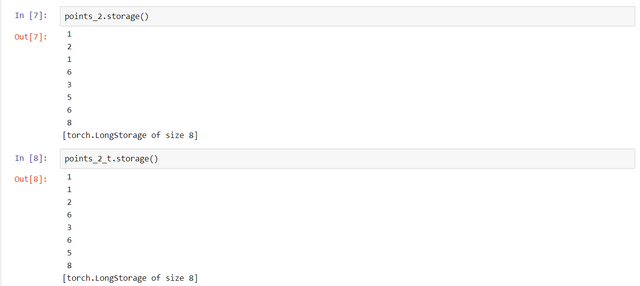
By the above example, we can see that when we apply .contiguous() function to tensor, it takes another memory space and makes a contiguous array.
Conclusion:
Here, we have shown some basic functions which relate to some core concept of PyTorch tensor like
* How tensor is stored in our memory
* Multiple views of tensors reference same storage
* How to transpose specific 2 dimensions from n-dimensional tensor
* How to clone a tensor
* How to make a tensor contiguous in our memory storage to make access efficient
I hope you like this blog. Thanks for your reading and please like if this blog is helpful for you.