Ernst Krenek's 1950 "Fifth Piano Sonata", Opus 121, presents challenges to layman and musician alike that, rather than diminishing its appeal, affirms its timeless worth. To those at the avant-garde of artistic inspiration and creation, the unprecedented destruction wrought by the Second World War served as an excuse to do away with all that went before, to treat all and sundry that smacked of tradition as indelibly tainted by the traumatic experience of the preceding decade. Hence one approaches the efforts of the Darmstadt School, its ranks dominated by such divisive personalities as Pierre Boulez, Bruno Maderna, Luigi Nono, and Karlheinz Stockhausen, as iconoclastic efforts predicated on a revolutionary disregard for traditional methods and principles.
Our composer Ernst Krenek, already in his fiftieth year at the time he composed his Opus 121, viewed with interest the developments emanating from Darmstadt, but despite some participation in their activities, he sought another path altogether. In his Fifth Piano Sonata, we do not uncover the processes of total serialism and other outré techniques mastered by the core of the Darmstadt School. Rather, Krenek, despite his long-lasting affiliation with and defense of the avant-garde, tempers the ideal of musical progress with a veneration for the canon preceding him, manifesting in his efforts to coalesce the traditional with the progressive in an organic, coherent way. In this, I argue, he succeeds, providing us an idiosyncratic masterwork that discloses the profundity of its composer's genius.
In the analysis below, I propose to render Krenek's tone row, the foundation of his composition, procedurally more comprehensible, and therefore enable greater appreciation of its structural and aesthetic characteristics. Moreover, I shall unveil the ways in which, through this work, Krenek "communicates" with a musical heritage that he loves dearly and wishes to preserve, despite the apparently wide gulf that has emerged between his methods of musical construction and those of his forebears. Rather than announcing the obsolescence of the old, Krenek invigorates it through new methods, thus honoring it in spirit.
In the first three measures of the first movement (marked allegretto con grazia, fairly fast and gracefully), Krenek provides us with a full statement of the tone row upon which the entire work's structure rests. Rather than distributing this initial tone row statement amongst multiple voices, which perhaps would enliven the texture but otherwise would obscure both performer's and listeners' awareness of its presence and intrinsic qualities, Krenek opts for a transparent and linearly-bound initial statement, one to which the inner ear may ascribe thematic significance as it is wont to do.

If one takes G as the starting pitch of this row statement, assuming that this is the prime form -- that is, neither retrograde ("backwards") nor inversion ("upside-down") nor retrograde inversion ("backwards" AND "upside-down") -- then the pitch class is {{0, 4, 3, 11, 6, 2, 1, 8, 10, 9, 5, 7}}. G is the first pitch of the row, thus we assign it the numeral zero. When calculating the distances by semitone of subsequent pitches in the row from the base G, we treat G as if it were the tonic of a twelve-tone scale and the subsequent row pitches as if appearing upwards rather than downwards in relation to this base G, even where the actual statement of the row's pitches does not conform to this assumption. Hence, B is four semitones away from G while B♭ is three semitones away from G. The process continues, with F♯ deemed eleven rather than one semitone away from G. Although the major seventh distance constitutes a larger absolute value than the minor second distance, the preference for eleven over one in this instance avoids confusion, proclaiming clarity in what otherwise may (perhaps unjustly) appear to be a forbidding musical-analytical task. The tritone (augmented fourth or diminished fifth) encompasses six semitones in either direction, hence the value assigned to C♯ in the row. A comprises the pitch class of two semitones, D♯ eight, F ten, E nine, C five, and D seven.


Thus, this particular ordering of intervals -- {{0, 4, 3, 11, 6, 2, 1, 8, 10, 9, 5, 7}} -- serves as the basis for the entire consequent musical composition, establishing order throughout, a sense of tight organization pervading the domains of melody, counterpoint, and harmony in spite of the absence of tonality in the strict sense. Where music once attained order -- and harmony -- through the exploitation of tonal gravity, of the hierarchies arising from the circle fifths as an emergent property of the overtone series, now tension and release obtain successfully through a twelve-tone organization. Even as the traditional fundamental polarities of tonic and dominant disintegrate in this evolution of the Western musical grammar and syntax, nature does not free the composer to employ mere arbitrary means.
This twelve-tone system, particularly when flowing from the pen of so illustrious a composer as Ernst Krenek, arguably prescribes a more intimate relationship with intervallic polarities than the earlier system of common-practice tonality. There is nearly a mystical quality inherent in this system of dodecaphony, despite the superficial appearance of arithmetical operations. Hence, the impropriety of the habit of the composer, performer, critic, dilettante, or music-lover in referring to twelve-tone composition, or dodecaphony, as "atonal" must reveal itself as a hollow pejorative, an unmerited dismissal of a valid technique by which the composer may attain musical expression. Despite the pervasiveness of dodecaphonic technical analysis, when accomplished with the heart dodecaphonic composition is of the heart.
Starting a measure after the right hand's initial entry, the left hand enters with its own statement of the prime form of the tone row. Although, as noted, the statement conforms to the pitch set {{0, 4, 3, 11, 6, 2, 1, 8, 10, 9, 5, 7}}, with total identity of the pitches maintained and transposition averted, the set undergoes an alteration in contour and rhythm. Hence, the first phrase expressed by the left hand begins on the second sixteenth note beat of the measure rather than on the first as in the right hand's initial statement.

Rather than ascending a major third to B, the G descends a minor sixth to the same pitch in octave equivalence. The retention of a subsequent descent of a minor second precedes another melodic contour inversion in relation to the melodic statement played by the right hand in the prior measure -- rather than descending a major third / diminished fourth (the latter being the enharmonic spelling), the left hand ascends from B♭ to F♯, constituting the leap of a minor sixth / augmented fifth (enharmonic spelling). Note, of course, that this works because the intervals of a major third and minor sixth exist in relation to one another as inversions of the other; essentially, they constitute the same interval in a transposed relationship, but the harmonic implications do not change. The left hand's "answer" in the opening measure's contrapuntal web preserves the descent of a perfect fourth from F♯ to C♯, yet the phrase ends with that same C♯, while the right hand's initial statement proceeds for another three pitches of the row to D♯.


G -- B


B --B♭
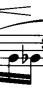

B♭ -- F♯


F♯ -- C♯


The rhythmic alteration coincident with the left hand's presentation of the tone row chiefly consists in the successive sixteenth notes of C♯ descending to F♯ undergoing partial augmentation in rhythmic value, as although the exact contour persists (as noted above), the F♯ sixteenth note in the right hand's statement becomes a dotted eighth note in the left hand. Nevertheless, the C♯ remains a sixteenth note, although immediately this pitch undergoes repetition in the next measure, appearing as a dotted quarter note (encompassing the complete metrical value of the measure, "filling out" as it were the two-measure phrase, delaying the appearance of the G♯ and D♯ that occupy the second measure of the first phrase of the right hand's initial tone row statement).



Curiously, the left hand's statement of the row does not constitute a complete treatment, as the composer omits the A interposed between C♯ and G♯ in the right hand's expository statement. Why Krenek in his discretion omits the A, the sixth and thus median pitch of the row, constitutes a worthy subject for speculation, and serves to remind those inclined to this subject matter that dodecaphonic composition is not mere science, is not immovably severe in its application of constructive principles to composition, as the total adherence to predetermined restraints without the incorporation of some degree of spontaneity or novelty necessarily leads to the sterility of invention of and expression. Though creativity requires constraints in order to thrive, too tight a straitjacket will asphyxiate ingenuity before the opportunity arises for its materialization. Granting the quasi-tonal implications of the row, the omission of this "median A" -- this pitch halfway through the row, nearly adjacent to its "leading-tone" G♯ -- may serve as a strategy on Krenek's part to circumvent the phantom of tonal gravity, rather than to indulge it as a composer of such stature as Alban Berg might.


While the right hand's row statement remains entirely linear-melodic, in the left hand (traditionally reserved for accompanimental or subsidiary material in idiomatic keyboard composition) Krenek permits himself the indulgence of harmonizing the row through activation of the vertical-harmonic plane of musical composition. Indeed, the F and E and the C and D that sounded successively in the right hand now sound simultaneously in the left, forming the dichords of a major seventh and minor seventh respectively. Although Krenek includes the first dichord within the second phrase of the tone row's left-hand statement, he isolates the second dichord, evading its phrasing within any melodic statement, thus for the first time in this composition relegating material to a subsidiary homophonic-accompanimental role rather than a truly polyphonic one. Note that the fact that the left hand's D is "below" the C, while the right hand's C "precedes" the D, does not violate any principle of dodecaphonic composition.


G♯ -- D♯


F -- E


C -- D


Interestingly, the rhythmicization of the G♯ and D♯ immediately preceding the F -- E dichord in the second phrase constitutes the first appearance of a divergence from rhythmic units based on multiples of two, as the G♯ -- D♯ succession occurs in the framework of a sixteenth note triplet.

One may detect in these initial melodic statements, despite their superficially "mathematical" qualities, a nostalgia for the old Hapsburg-ruled Austria of Ernst Krenek's youth, one long since passed into oblivion by the time that Krenek, residing in the United States of America and acclaimed there as both composer and scholar, set pen to paper in the composition of this piano sonata five years after the closing of the Second World War.
Let us take the first phrase of the right hand's statement. Already there are subtle tonal implications that even Krenek in his devotion to the dodecaphonic system cannot completely suppress. The first two pitches, G and B, a major third apart, form the first two pitches of the G major triad and the second two pitches of its relative minor, the E minor triad. As the starting pitch is G, a stronger case surfaces for an implied tonality of G major. Nonetheless, while tonal phantoms already lift their heads, substantial tonal ambiguity exists. And what of the following pitch, the B♭? This might suggest a sudden flattening of the implied G major tonic to G minor, a tonal tug-of-war redolent of the hypertrophied tonality of Late Romanticism, in which stylistic milieu Krenek contributed his first compositions under the tutelage of his teacher the arch-Late Romantic opera composer Franz Schreker. In any case, this unadorned, unaccompanied line exudes "color" merely through this minor second descent preceded by a major third ascent, and this color-intuition emerges out of a repressed memory of the once-assured permanence, stability, and totality of common-practice tonal function, the kingdom of tonic and dominant.

Considered in the context of the subsequent three pitches in the first measure, the aforementioned B♭ assumes a new meaning. Perhaps the B♭ is an enharmonic spelling of A♯. In light of the succeeding pitches F♯, C♯, and A, we confront yet another tug-of-war between major and minor modes. The descending A♯, F♯, and C♯ spell out a second inversion F♯ major triad; the descending F♯, C♯, and A spell out a first inversion F♯ minor triad; meanwhile, treating all four pitches as constituents of a single tetradic chord, we uncover a chord of both Late Romantic richness and Early Modern high tension, one we may name an F# dominant seventh with added natural tenth.



However, in a more conservative harmonic context, that A would likely serve as a non-harmonic tone, a passing note impliedly resolving downwards. Indeed, this A natural precedes a G♯ in the following measure, this G♯ integral to the opening phrase. Hence, a subtle implication might arise that this sequence of pitches -- A♯, F♯, C♯, A, AND G♯ -- spells out and ultimately insinuates, no matter how inadvertently (or perhaps subconsciously for the composer himself), an F# dominant seventh sharp ninth chord with passing natural tenth resolving immediately downward to the sharp ninth. Simplified, this constitutes an implied F# chord of dominant character, preceded by an implied G major -- or minor, or both -- dichord.


The relationship between chords of G and F♯ is most persuasively that of G as a flattened supertonic; that is, G major as the Neapolitan of F♯ major, BUT with the caveat that here F♯ appears in dominant guise, suggesting a concealed tonic of B major or minor. The appearance of a D♯ following the G♯ lends some credence to the thesis that the concealed tonic is B major. A convincing argument arises that this G♯ -- D♯ pitch sequence, while affirming the B major tonality, further implies a deceptive cadence wherein the V chord (the dominant, F♯) resolves not to the expected I (the tonic, B) but instead to the ii (the minor supertonic, G♯ minor, a triad comprised of the pitch sequence G♯ -- B -- D♯, thus containing the tonic pitch as its mode-determinant third).


Of course, this is not to say that Krenek's piano sonata is a tonal work per se. I do not mean to suggest that Krenek intends to convey a sense of latent tonality beneath the surface of an ostensibly dodecaphonic work. After all, the purpose of the dodecaphonic system is to avoid what the composer perceives to be the formulae of an exhausted system of tonal organization. Yet the suggestion of an older style within the metes and bounds of a newer method neither obviates the effectiveness of the earlier method nor eradicates its aesthetic necessity. A work of art may exist on multiple planes of analysis and thus may contain within itself multitudes of meaning. The apparition of conservative tonality within a radical dodecaphonic framework does not attest to the failure of the latter but instead reaffirms the validity of the latter as a natural extension of the former.
Moreover, one may wrest another indication of Krenek's latent nostalgia for the old aristocratic Austria of his youth from the contour of his opening right-hand phrase. First, observe that the time signature is 3/8 (a triple time-variant, one less common than 3/4 but still not too alien to ordinary sensibilities). Although Krenek notates his time signature in a somewhat heterodox manner, he conveys his intent clearly. The mellifluous thirds of his melodic contour, so suggestive of the tonality of a bygone era, suggest many a classic waltz by the Strauss family of Vienna. And, indeed, the ländler, an Austrian folk dance which later birthed the aristocratic waltz, often operates in 3/8 time, and in such a relaxed yet vital tempo as allegretto. Whether waltz or ländler, such Austrian triple-meter dances characteristically feature elegant, sensual contours as Krenek writes here.
The analyst may roughly analogize the melodic contour of Krenek's opening phrase with the third complete measure of the first of the pianoforte Waltzes, Opus 39, composed by Johannes Brahms. Both melodic fragments materialize as swooping curves in triple time, although the exact intervallic characteristics differ between Brahms and Krenek. In Brahms' example, a descending minor second precedes two descending major seconds and two ascending major seconds. Krenek's intervallic stretches are wider for the most part. In this opening right-hand phrase Krenek begins with a rising major third, followed by a descending minor second, descending major third / diminished fourth, descending perfect fourth, and descending major third. Nonetheless, the descending sequence of the last five pitches of Krenek's measure mirrors the descending sequence of four pitches that opens the measure by Brahms, while the ascending two pitches that open Krenek's measure find their echo in the ascending three pitches that close the example from Brahms. Incidentally, the B major tonic of the Brahms example curiously echoes the implied B major tonic in the Krenek as suggested above.
Brahms

Krenek

TO BE CONTINUED ....
Sources:
(1) http://en.scorser.com/Out/300566341.html
(2) https://ks4.imslp.info/files/imglnks/usimg/f/f8/IMSLP84174-PMLP06507-Brahms_Werke_Band_14_Breitkopf_JB_61_Op_39_filter.pdf