Euclidean Geometry
Euclid's "Elements" is one of the most famous works in human history. The uprising dates back to the 4th century BC. This book dealing with geometry, arithmetic and shaped the thinking of many eminent scientists, such as Newton and Galileo. It was created in a deductive form. Euclid adopted set of axioms on the basis of which he logically derived theorems. In this way he derived practically all geometry and ancient arithmetic. From planimetry to elements of modern number theory.
There were five of them, and they sound like this:
I. If we have two points, we can connect them with a straight line.
II. If we have a straight line, we can extend it to infinity.
III. If we have a line, we can draw a circle centered at any point on the line with a radius equal to that line.
IV. All right angles are equal to each other.
V. If two straight lines intersect the third in such a way that the sum of the interior angles on one side is less than the two right angles, then if they are extended sufficiently, they will intersect.
________________________________
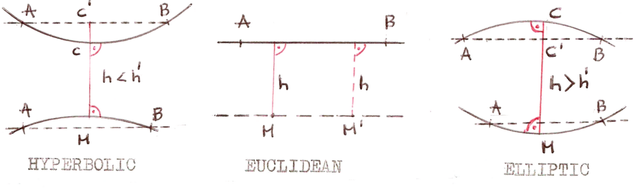
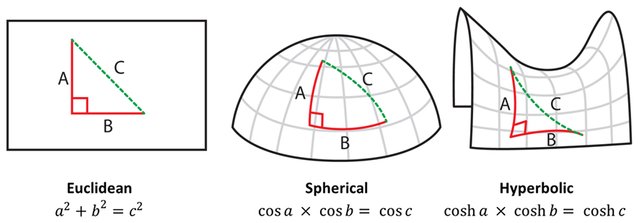
The first four axioms are clear and understandable. If we talk about fifth axiom, we can have doubts about it. For a long time mathematicians have tried to prove that Euclid's fifth axiom can be deduced from the previous four. If they were successful, we could throw him out of this list because he would not meet the definition of an axiom (an axiom cannot be proved by other assumptions). It turned out later that it was not dependent on other axioms and stayed where it was. The model of geometry that takes 5 Euclid's axioms is called Euclidean geometry. We can learn this geometry at school in the first math lessons and use it when we choose furniture for our room or when we need to draw a square. A characteristic feature of Euclidean geometries is the fact that the sum of the angles in a triangle is always 180 degrees. This is important. Let's remember it. Therefore, it describes our everyday world very well. Great example is that classical Newtonian mechanics works.
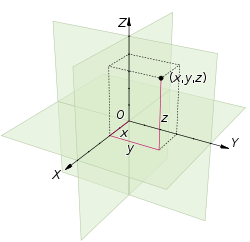
Euclidean Space
When Newton, unifed the laws of motion describing the motion of a cannonball with the mechanics of the sky, leaned the entire theory on the Euclidean geometry. He placed the model in which he described his physics in Euclidean space. Flatness is a characteristic feature of this space. To understand what this means, we can consider spaces with a different number of dimensions. For example, one-dimensional Euclidean space is straight, and two-dimensional is a plane. We call it linear space. If we draw a coordinate system where each axis is perpendicular to each other, it will be an example of a linear space. We can write the fifth axiom in a slightly different form.
If we have a straight line, then only one straight line can be drawn for a given point, such that both are disjoint.
This means that two parallel lines will never intersect. If they are not parallel, just extend them and they will eventually cross. While working on the independence of the fifth axiom, mathematicians noticed that when we replace it with its negation, we get a different coherent model of geometry. On further analysis, they concluded that there were two possibilities. * If we have a line, we can draw an infinite number of disjoint lines through the point lying on it, or we cannot make any disjoint line. * The first case was described by such mathematicians as Carl Friedrich Gauss or Nikolai Lobachevsky and thus created hyperbolic geometry. The second case was analyzed by Bernhard Riemann, the creator of elliptical geometry. This models are build on modified Euclid's axioms. We call such geometries non-Euclidean.
Elliptic Geometry
The elliptical geometry model abandons Euclid's fifth axiom. It follows that if we have a given straight line, then for any point chosen by us there is no straight line that passes through this point and is separable from our straight line. This means that every two lines intersect at some point. Therefore, there is no such concept as parallelism in the model of this geometry.
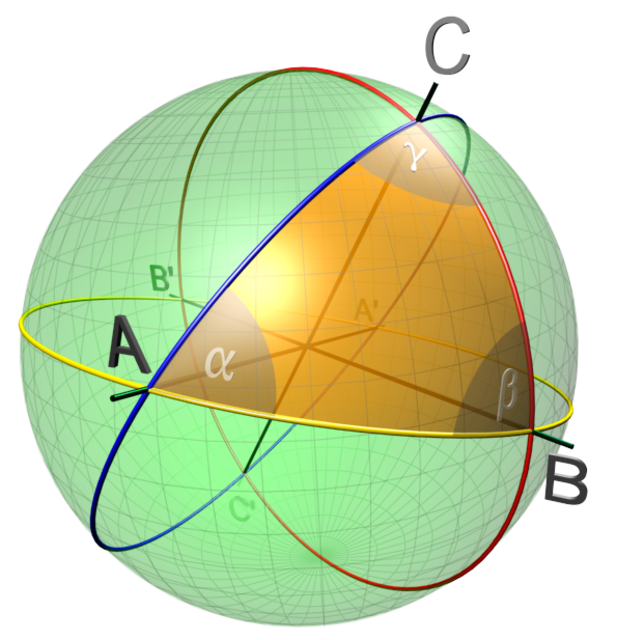
To visualize this type of geometry, we can imagine lines lying on a positive-curved surface or on a sphere. We identify a point with a pair of two antipodic points (points located opposite to each other on a sphere). With the concept of a point defined in this way, a straight line corresponds to a set of pairs lying on a great circle, and to a plane, a set of all such pairs of points. The segment, on the other hand, is an arc connecting two points lying on the great circle. Now let us recall what was the sum of the angles in a triangle in Euclidean geometry.
In elliptical geometry, the sum of the angles is always greater than 180 degrees! (a triangle on a spherical surface has curved sides outward).
In elliptical geometry, the sum of the angles is always greater than 180 degrees! (a triangle on a spherical surface has curved sides outward).
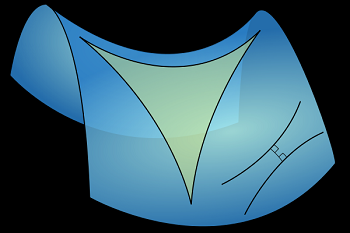
Hyperbolic Geometry
In the hyperbolic model, we do not abandon the fifth axiom, but modify as follows.
If we have a straight line and we choose any point, then at least two straight lines that have no common points with our line pass through this point.
Unlike elliptical geometry, the hyperbolic model has a negative curvature. Imagine a saddle-shaped surface. The assumptions of the hyperbolic model result in many properties completely different than in Euclidean geometry. For example, for any angle there is a straight line that is parallel to both of its arms. A point is interpreted in a classical way, and a straight line is an arc that is perpendicular to the edge of the circle. A plane in hyperbolic geometry is defined as a circle without an edge, and a segment is a fragment of an arc perpendicular to the edge of the circle, which is contained between two points. As for triangles, however:
In hyperbolic geometry, the sum of the angles in a triangle is always less than 180 degrees!
Thank you for paying attention.
Greetings!
Sources: 1 2 3 4 5 6 7




For more,you can visit this community
JOIN WITH US ON DISCORD SERVER:
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You have been Upvoted @steemitinland. You can support us by delegating your idle sp. You can delegate in our community by clicking through these links.
in
Discord Server
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit