Inviting all Steemians to the Steemit Learning Challenge Season 23

In school, I wasn’t particularly fond of mathematics. I was more drawn to computers, but during my time at the institute, I grew to like math, and recently, I’ve developed a special interest in geometry.

With the advent of computers, I dreamed of a program that would allow me to create beautiful drawings for geometry problems—and such a program has appeared: it’s called GeoGebra.

We all studied mathematics in school—algebra and geometry. With the formation of families and the arrival of children, some of us revisit those school lessons while helping the little ones with their homework. I, too, suggest reminiscing about school years and diving into the realm of mathematics, into geometry.

GeoGebra

As you can see, this word is formed from two words: Algebra and Geometry. So, let's go to the website www.geogebra.org

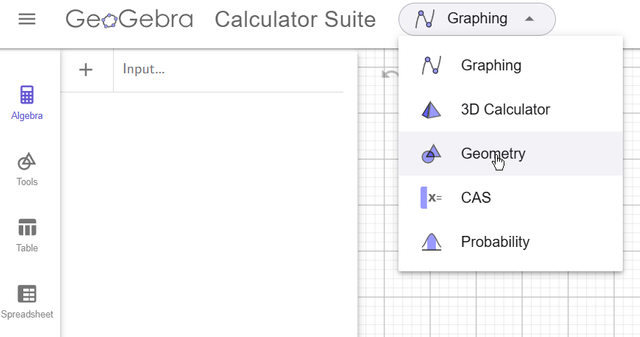
Even if you go to the website using the link, you should still select Geometry.

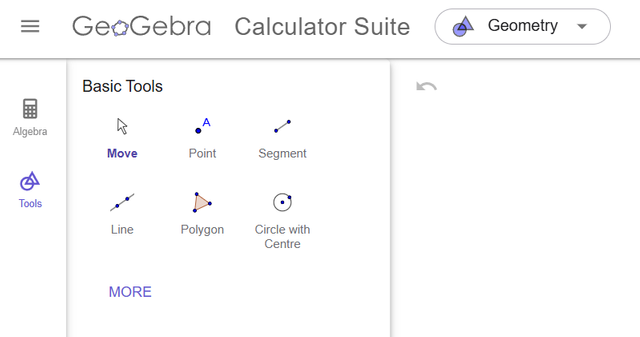
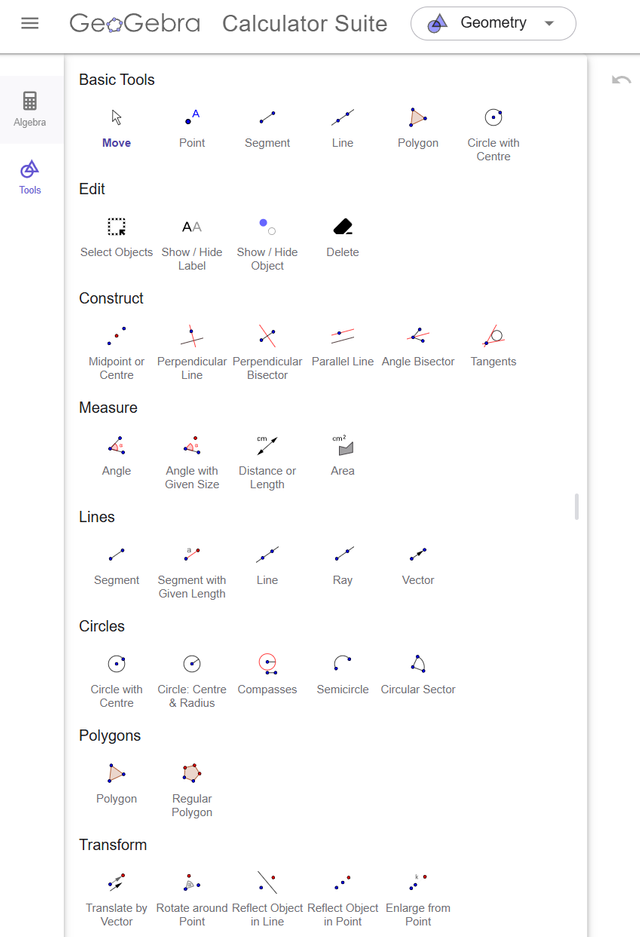
After this, not all tools are displayed—very few are shown. By clicking MORE, more tools open up, but to see the rest, you’ll have to click MORE again.

1. Point

One of the fundamental concepts in geometry is the point. A point has no dimensions and is denoted by a capital Latin letter. It is the building block for other figures.

2. Line

A line is a collection of points that extends infinitely in both directions. It has no beginning or end, no thickness or width. It is denoted by two capital letters or a single lowercase Latin letter. Only one line can pass through two points. Two distinct lines either do not intersect (they are parallel) or intersect at a single point.

3. Ray

A point divides a line into two rays. A ray has a starting point but no endpoint. It is denoted by two capital letters—the starting point and any other point on the ray.

4. Segment

A segment is a part of a line—it has a beginning and an end. It is also denoted by two capital Latin letters.

5. Intersection Points

If you construct two intersecting lines (or segments), the intersection point will not appear automatically. For this, there is a special tool—the intersection point.
Blue points can be moved (unless explicitly restricted), while black points, which are automatically created during construction, cannot be moved directly or arbitrarily.

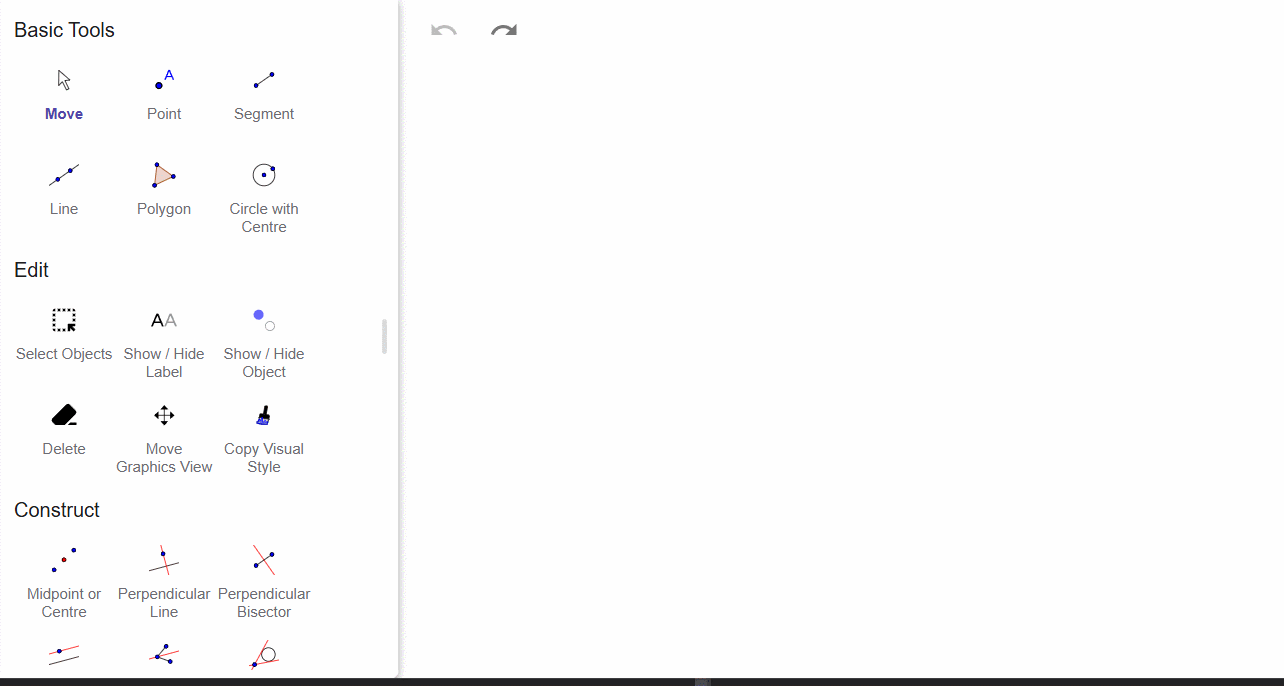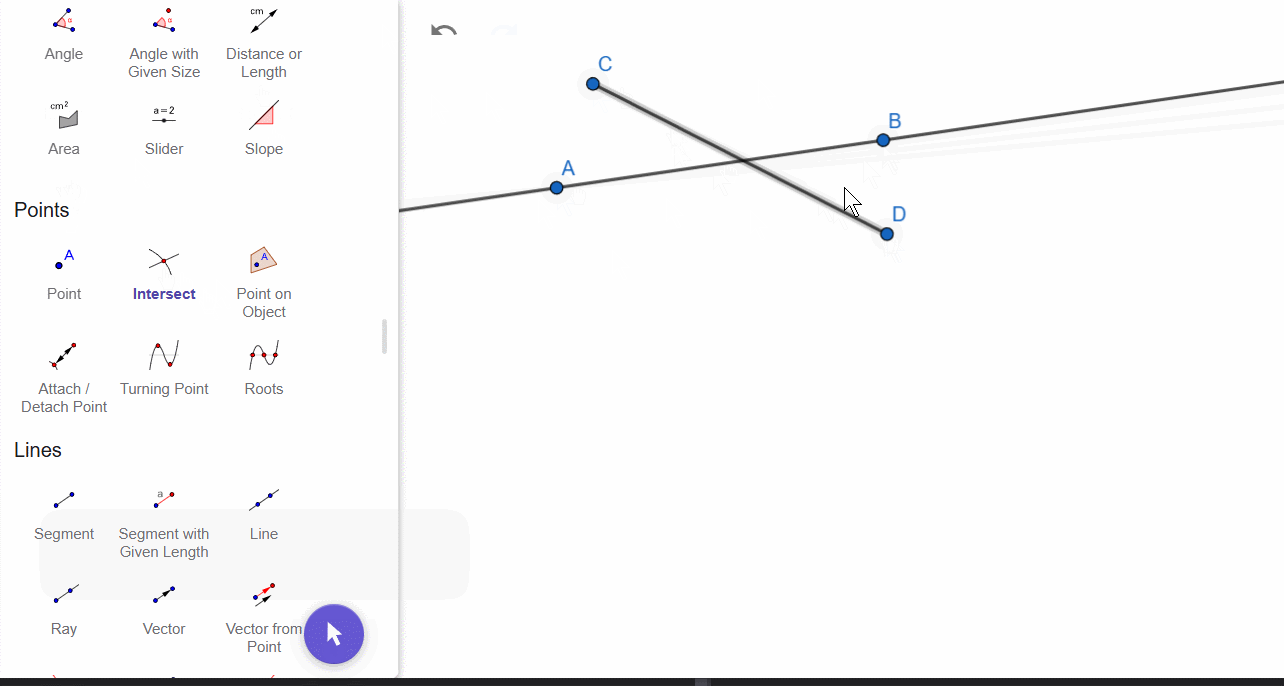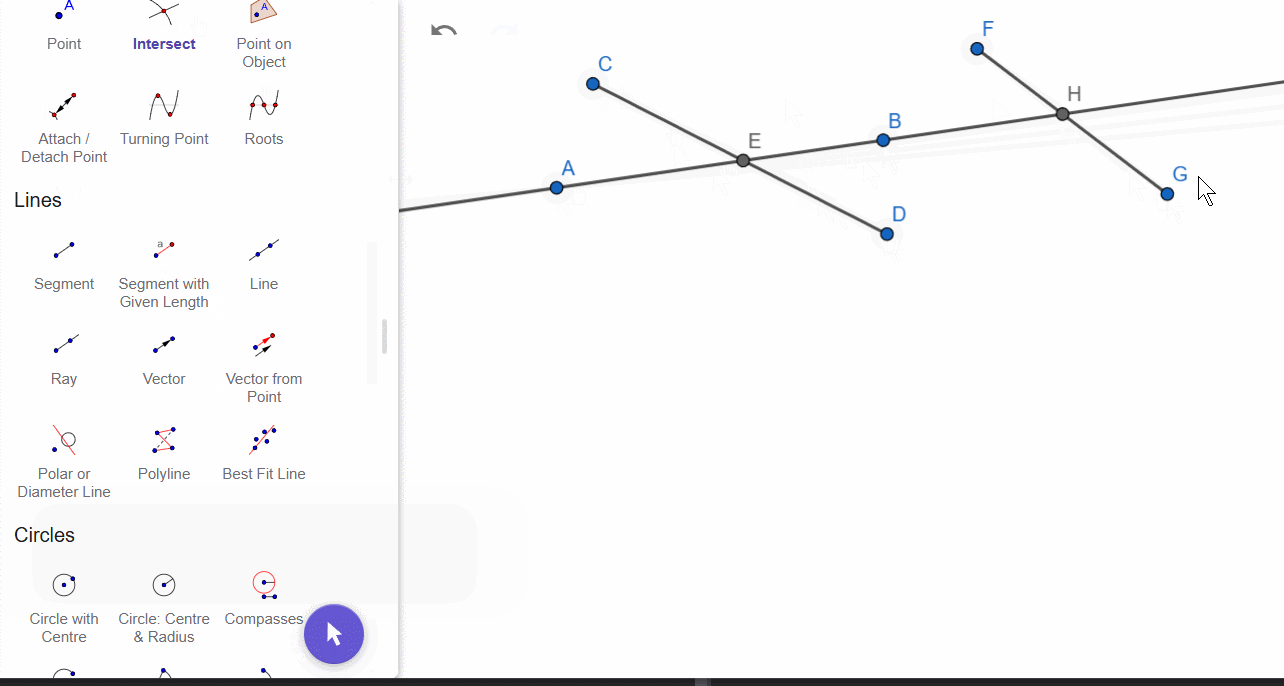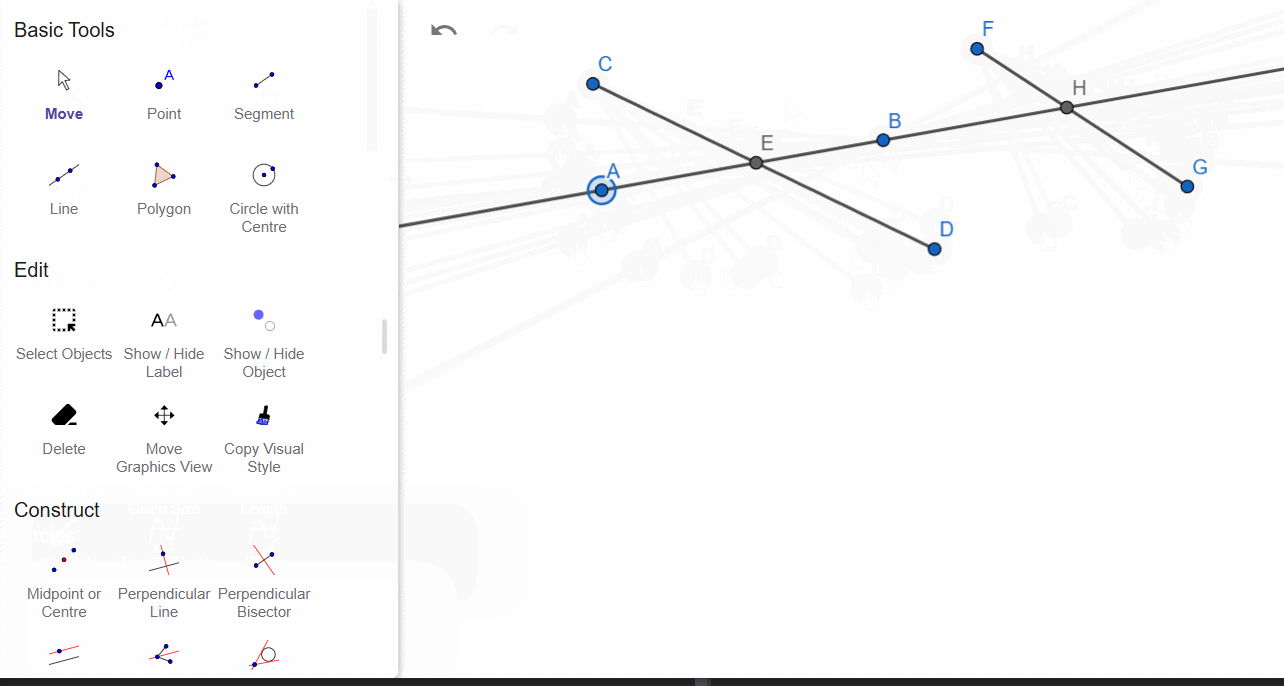
Intersection points can be constructed in two ways:

1. Select the first figure and then select the second figure—this will display all intersection points.
2. Click approximately at the intersection location—this will create the specific intersection point.

It is important to distinguish between the intersection of segments and the intersection of their extensions. To construct the intersection point of two segments (even their extensions), you need to:
Construct the lines that contain these segments, build the intersection point of these lines, then, you can hide the lines themselves.

6. Angle

An angle is a figure formed by two rays that originate from a single point. Each angle has a specific degree measure. The degree measure of an angle is the sum of the degree measures of the angles into which it is divided by any of its rays.

7. Adjacent Angles

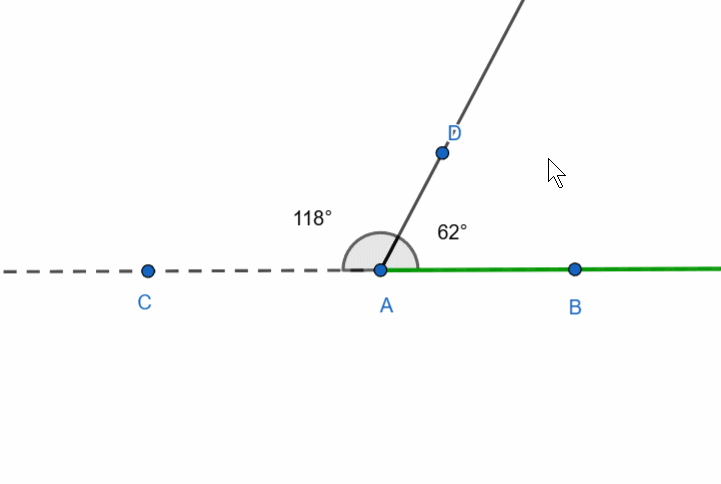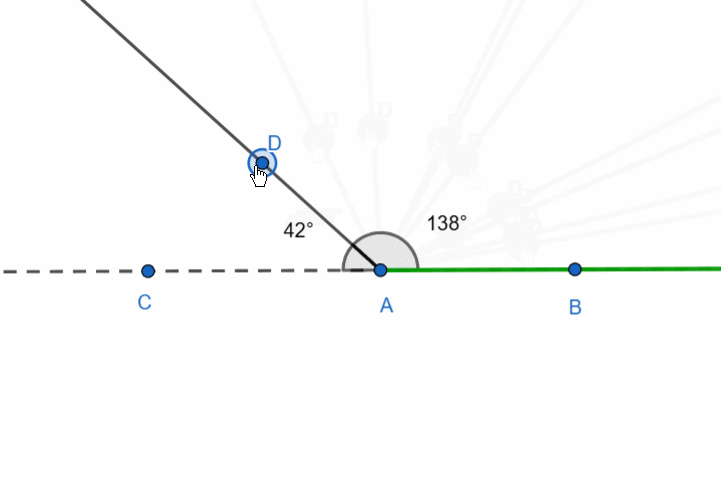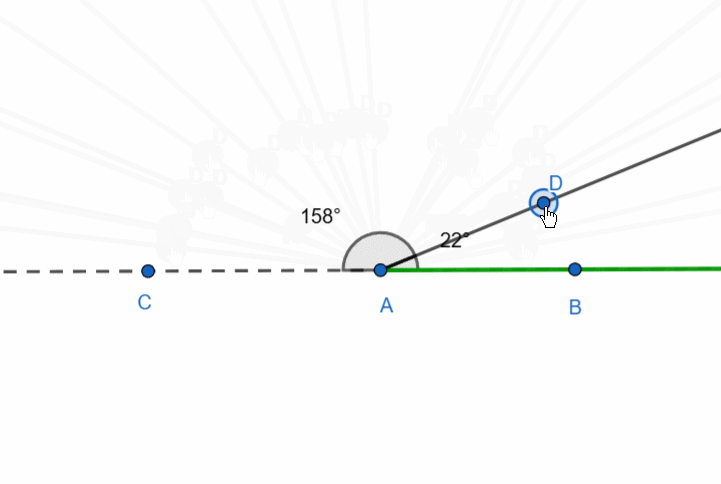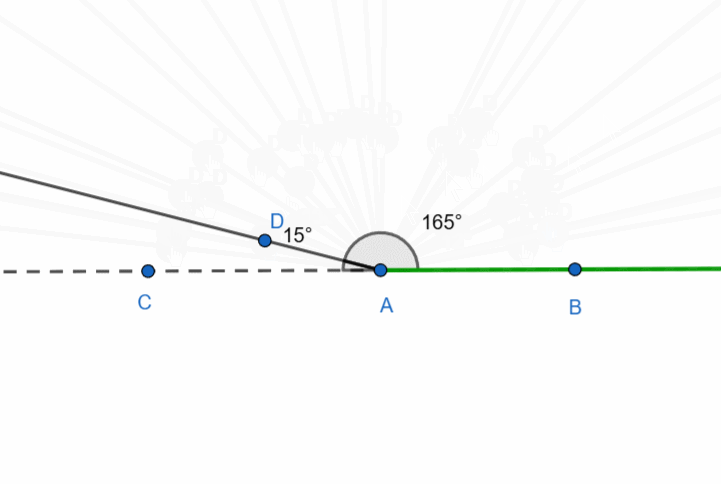
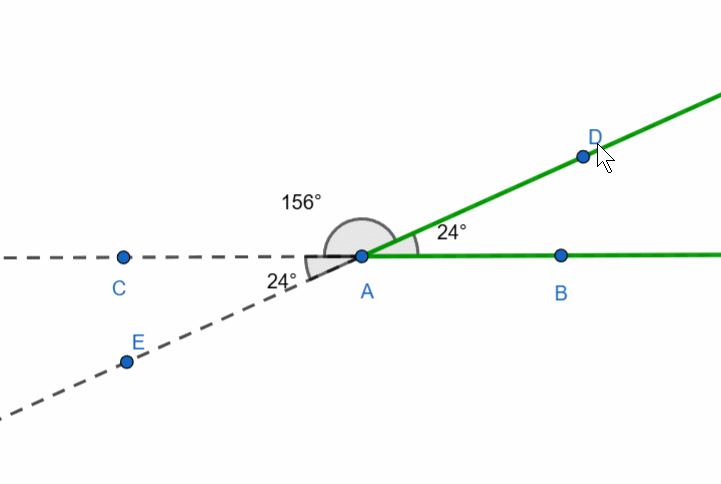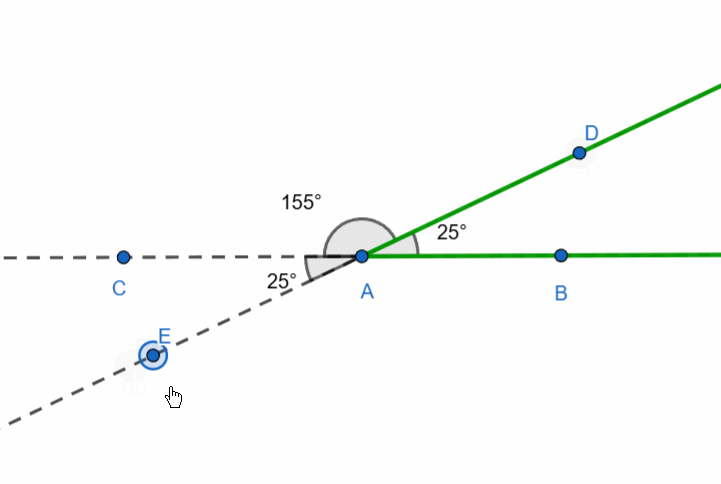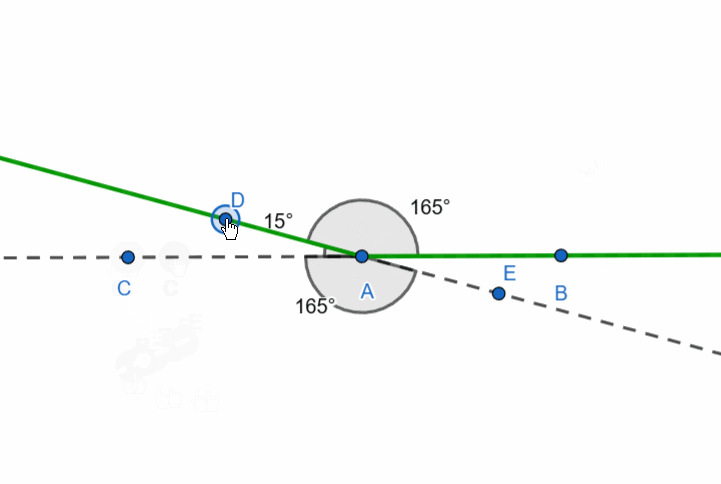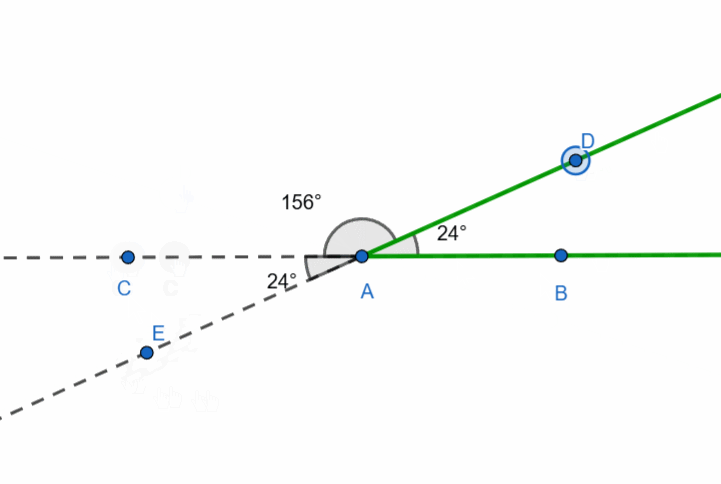
There is also the concept of a supplementary ray. If we have a ray, we can draw many other rays from its starting point, but only one will form a straight line with the given ray—this is called the supplementary ray.
In the figure, the dashed ray AC is supplementary to the green ray AB.
The degree measure of the angle formed by a ray and its supplementary ray is 180 degrees.

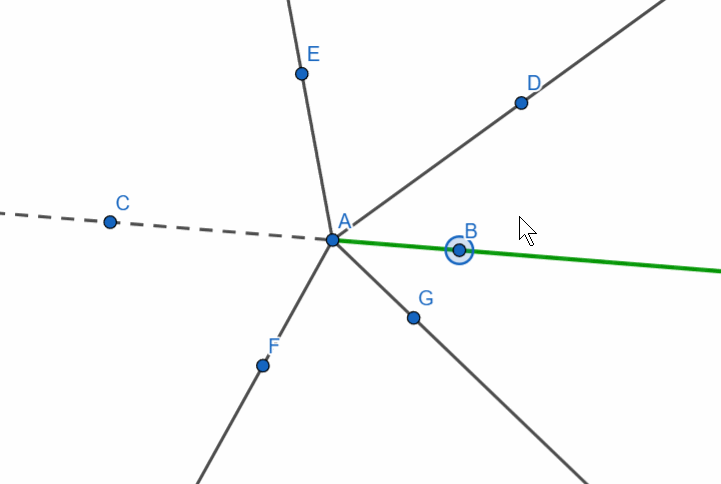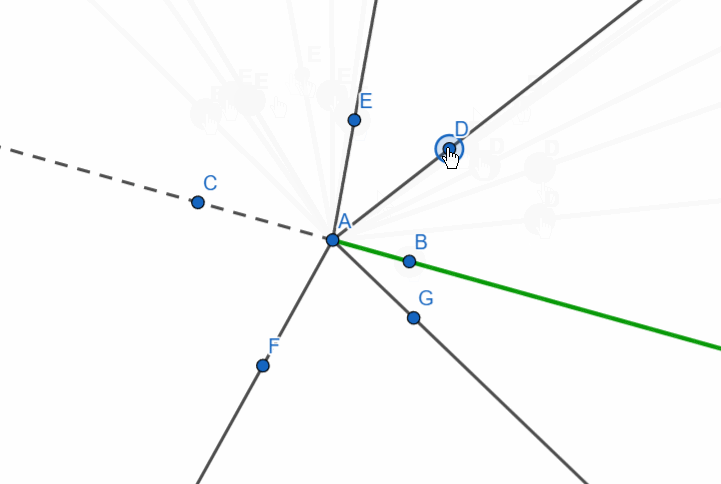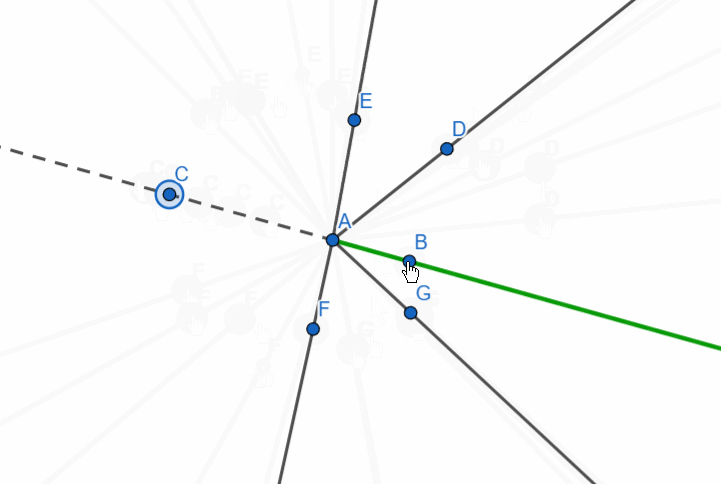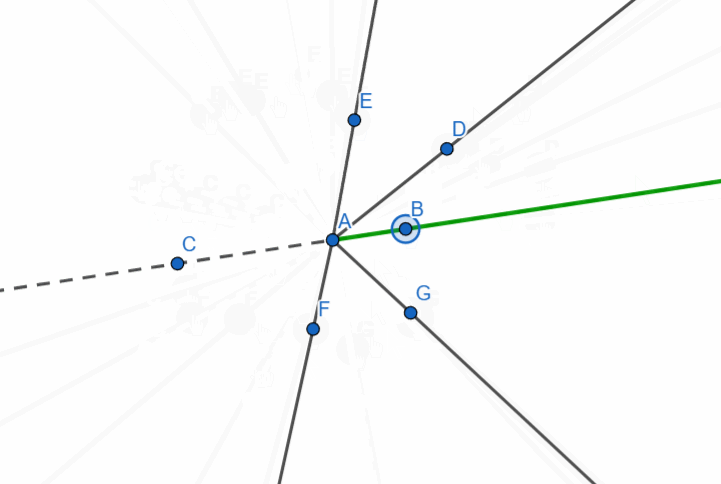
Let’s now consider the following figure: three rays originate from a single point. These are ray AB, its supplementary ray AC, and an arbitrary ray. It looks as though the straight angle is divided by a ray.
The sum of adjacent angles is 180 degrees.

8. Perpendicular and Parallel Lines

If two adjacent angles are equal, their measure is 90 degrees, and they are called right angles. If the angle measure is less than 90 degrees, it is called an acute angle; if it is greater, it is called an obtuse angle. Lines that intersect at a right angle are said to be perpendicular.

If two lines do not intersect, they are called parallel lines.

There are two corresponding tools that allow you to draw a parallel line and construct a perpendicular line.

Perpendicular Line

Parallel Line

Let’s consider two arbitrary lines a and b intersected by a transversal c.
At the intersection, eight angles are formed, and there are even more pairs of angles.

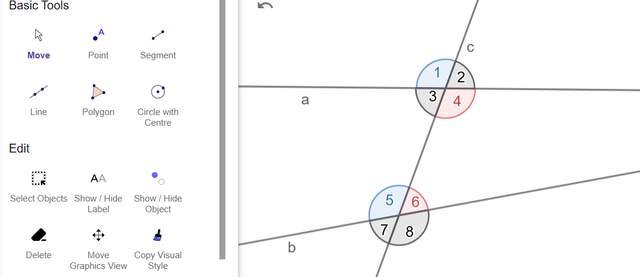
(1,4) (2,3) (5,8) (6,7)	vertical angles
(1,2) (3,4) (1,3) (2,4) (5,6) (7,8) (5,7) (6,8)	adjacent angles
(4,6) (3,5)	interior samesided angles
(3,6) (4,5)	interior differentsided angles
(1,5) (2,6) (3,7) (4,8)	corresponding angles

Homework

Task №1

What is geometry? When and why did it appear? How did you study geometry in school? Were you familiar with any geometry software?

Task №2

Explain different geometric primitives (point, line, angle, segment, ray) and illustrate them in GeoGebra.

Task №3

Construct an arbitrary angle, then extend one side to create a supplementary ray—show that the sum of adjacent angles is always 180 degrees.

Construct an angle with two supplementary rays—show that the resulting vertical angles are always equal.

Task №4

Construct parallel lines and perpendicular lines.

Construct two lines intersected by a third line (a transversal). Label the angles on the figure (using letters, numbers, or colors). Name the pairs of angles that have special names.

Task №5

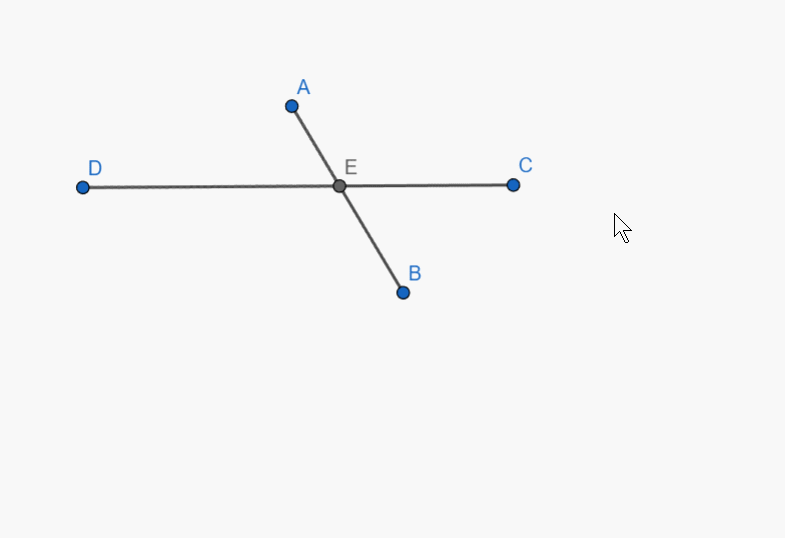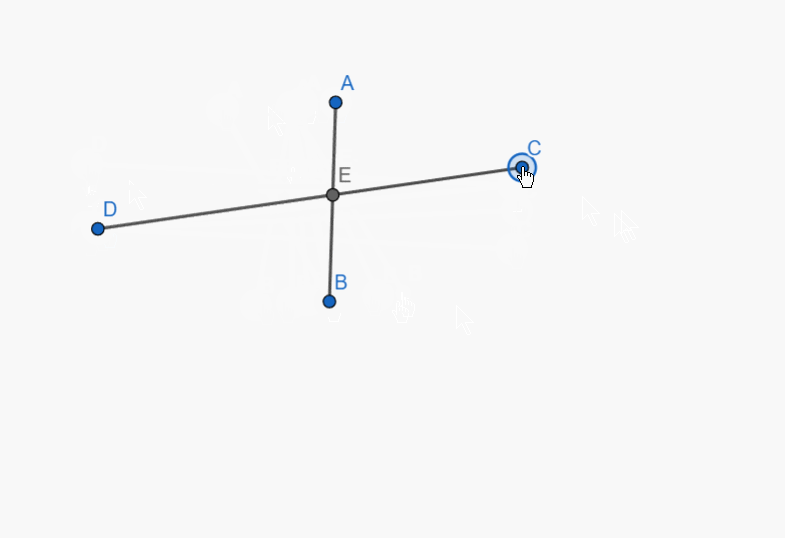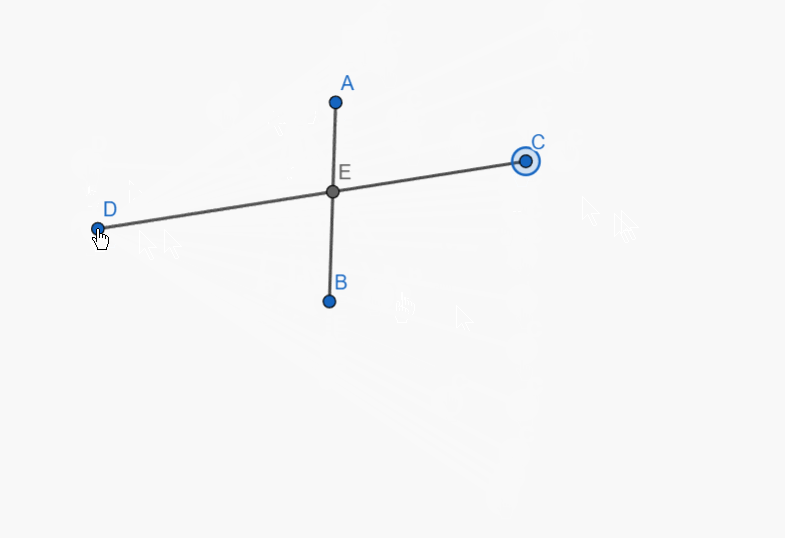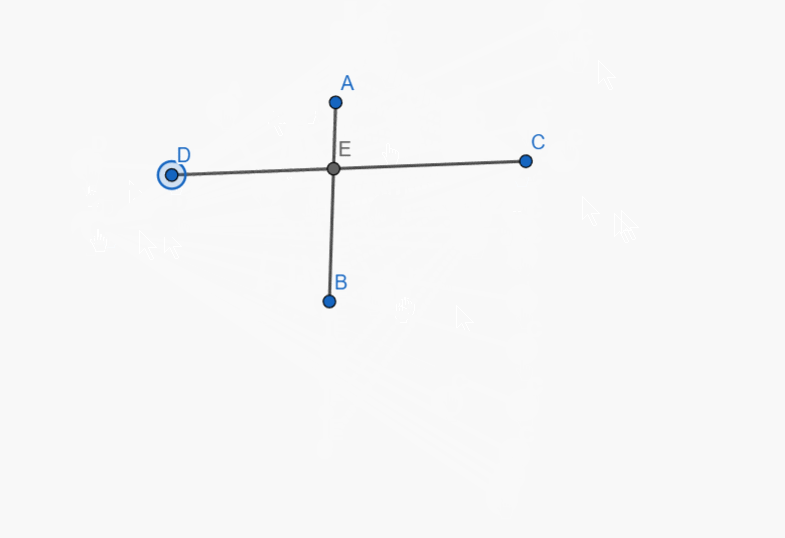
Construct the intersection of two segments. Ensure that the intersection point is always displayed, even if it does not lie on the segments themselves. If the intersection point lies outside the segments, represent this with dashed lines.
As I demonstrated here.

Each task 2 points. Beauty, accuracy, creativity will also be evaluated

Rules for Participation

Title of your work: SLC S23 Week1 || Geometry with GeoGebra: Points, Lines, and Angles

You can publish your work in any language, in any community, or simply in your own blog. Add the link to your work below as a comment.

To help me quickly find, review, and evaluate your work, leave the link in the comment under this text, and in your work, use the tag #gwgg-slc23w1

Each task response must include at least one image and one video (GIF) demonstrating the process of construction/solving.
You can use tools like GifCam as I did.
Note: The video/GIF will have the most significant impact on the evaluation.

Plagiarism and the use of AI are prohibited.

Participants must be verified and active users of the platform.

All images used must belong to the author or be free of copyright. (Don’t forget to credit the source.)

Participants must not use any bot services for voting or engage in vote buying.

Recommend your friends to participate.

Submission Period: From Monday (February 17/2025), to Sunday (February 23/ 2025).

Your work will be reviewed, commented on, and evaluated by me. Four best works will be selected.