Hi @khursheedanwar. Thank you for granting me this privilege to partake in this algebraic expressional problems. I'm @deetalka6, lover of mathematics and further mathematics. I want to use my little knowledge to express in your assignment here.
Let's start.

Explain difference between linear and quadratic equations. Provide examples of each type of system of equation and describe their general forms.

S/N	Linear equations	Quadratic equations
Uniqueness 1	The word Linear implies Single. Single means 1	The word Quadratic implies unisex or married. For example, man + woman = couples. Couples can be quadratic in the sense that they are no longer one but two.
Uniqueness 2	Linear equation has the highest power of the variable 1	Quadratic equation has the highest power of the variable 2
Uniqueness 3	We can use either Addition, Substraction, Multiplication or Division method to tackle Linear problems	We can use Factorization, Completing the square method, General quadratic formula and Graphical method to tackle quadratic problems
Uniqueness 4	Linear equations are presented as: 2x + 3 = 5	Quadratic equations are presented as: x² + 4x + 4 = 0
Uniqueness 5	In Linear equations, there's no much consultation when solving	In Quadratic equations, you have to consider the following: constant term and algebraic variables. For example: x² + 4x are algebraic variables, while 4 is constant term. So constant term during the use of completing the square method can be switch across the equal sign. That is: x² + 4x = –4.

---

Describe methods for solving quadratic equations

Factorization method: This is the simplest method in Quadratic equation. It would only seem difficult for those who do not want to spend time and study the flowchart of the formula. Once you master the techniques or approaches applied for easy calculation here, then you would be able to tackle problems using this method.

To factorize simply means to **search for two numbers that when added or subtracted gives birth to the second variable, and when multiplied gives birth to the constant term.

Example: x² + x - 6 = 0

x is the second variable which is to be factorized.
-6 is the constant term which is to be factorized.
x = 1.

Therefore, the two numbers needed to factorize the above variables is: –2x+3x = +x.
While –2 × 3 = –6.
That is: x(x–2x)+1(x+3)

The Pros:

Anyone can learn this method and master it without getting stress. Once you understand the principles of your multiplication table, then you'll be able to solve them.

The Cons:

If you don't master your Multiplication table very well, you will have problem with generating of numerable factors.

Completing the Square method: This one is more technical. There are certain principles that govern this. Understand the principles, and then you're good to go. For example: 2x² + 4x + 6 = 0

1. Separate the constant term from the variables.
   2x² + 4x = –6

2. Reduce the coefficient of the term by dividing both side by the variable of x² which is 2.
   2x²/2 + 4x/2 = –6/2
   x² + 2x = –3

3. Add the square of half of the coefficient of the linear term to both sides (1/2 × 2x)² = x²
   x² + x + (x)² = –3 + (x)²
   (x–x)² = –3 + x

4. Take the square root of both sides and solve the equation:
   √(x–x)² = ±√–3+x
   x–x = ±√–3+x
   x = x+ √–3+x or x–√–3+x

The pros:

Just master the principles, you are good to go.

The cons:

If you don't master the principles, you will never be able to solve that problem.

Quadratic Formula: This one is the simplest method. Just master the starting point, and you're good to go. It uses alphabets a, b and c to represent the variables and the constant term.
For example: 2x + 3y + 4 = 0

Quadratic Formula made it as easier as:
a = 2
b = 3
c = 4

Using the Equation, –b±√b²–4ac ÷ 2a.
Just pick the numbers above and locate their positions in the equation.

The Pros:

Just master the instructions, you are good to go. With this method, you can solve any quadratic problem. Be it hard or simple.

The cons:

Failure to master the instructions make it more difficult.

Graphical method: Just know the value of x at initial and x at final. Do same for you. Be able to determine the units you're to used for both directions from any equation given. Y axis and x axis.

The Pros:

When you are able to determine the units for each axis, you won't find it difficult during plotting. Because, plotting graph is a transfer of your data's both for y and x axis on the graph.

The cons:

If you don't know how to find or calculate the unit for each axis, get a tutor if not, you won't be able to represent the results you've gotten in graphical representation.

---

Task 3

The first one is Linear equation and I got 3 as the value of x via subtraction method.

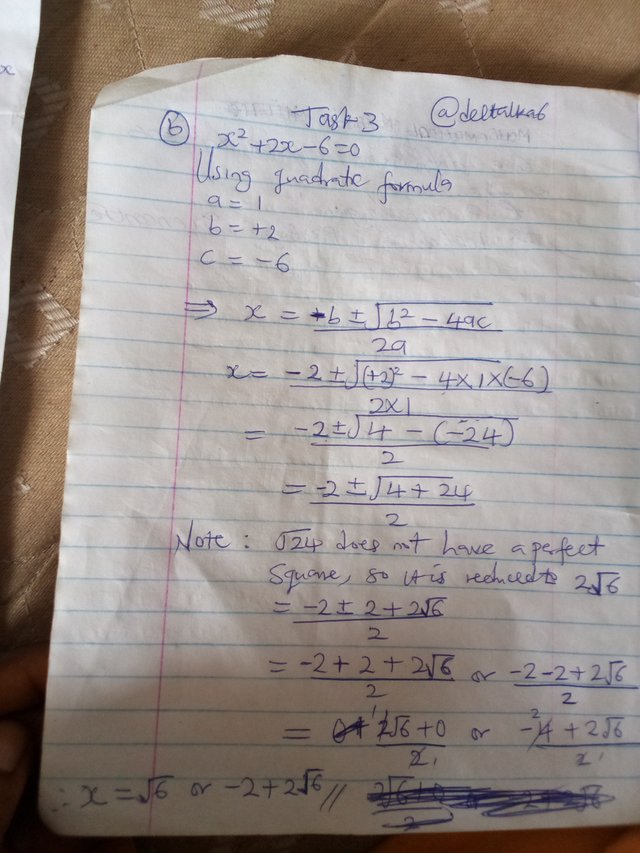
The second one is quadratic equation and I used the Quadratic Formula to aim at the result.

Task 4

Scenario number 1:

Suppose Ali have $15 for spending at snacks. He is buying a pack of chips for $3. How much money he have left?

Let x be the money left. Equation: x + 3 = 15.
Check the picture above for the calculations.

Scenario number 2:

Suppose there's a ball which is thrown in upward direction from ground with initial velocity of 20 m/s and height of ball above ground is presented by following equation;

h(t) = -5t^2 + 20t

Here h is height in meters and t is time in seconds.
Check the picture above for the calculations.

I give 25% to @null acounts

I invite @bossj23, @nemerem01, and @ngoenyi to participate in this contest.