Greetings steemians, here is my entry for the SLC S22W4 on Linear and Quadratic equations. Linear and quadratic equations is one aspect of algebra that can help in problem solving and a well as running some applications. Now here’s the answers to the questions asked at the end of the class.
TASK 1
Explain the difference between linear and quadratic equations. Provide examples of each type of system of equation and describe their general formula.
The number of variables contained in Linear equation and quadratic equation is what makes the difference. Linear equation has only one variable (usually x) while a quadratic equation has two variables.
Linear equation: a typical algebraic example of a linear equation can be expressed as thus; 2x + 3 = 7.
The general formula of a linear equation is written as: ax + by = c
Quadratic equation: the general form of a quadratic equation can be written as; ax^2 + bx +c = 0
Quadratic equation is more complex compared to linear equation. An example in algebra can be written as; x^2 + 4x + 4 = 0
TASK 2
Describe methods for solving quadratic equation, share pros and cons.
Below are the common methods that can be applied to solve a quadratic equation
Factoring method: this method helps us to express quadratic equation as a product of two binomials. The sets of the binomials is equal to 0 while solving for x.
Pros:
- it is easier to use because it’s a straightforward method
- No complex formula to memorize.
Cons:
- this method cannot be used to solve large coefficients.
- It is only applicable to quadratic equations that can be expressed as products of two binomials.
Quadratic method: this has to do with using the general quadratic formula to solve the quadratic equation. The formula is x = (-b ±√ (b^2 – 4ac). The value of a, b, and c must be plugged into the formula for accuracy.
Pros:
- this method works for all quadratic equation.
- It is easy to plug values into the quadratic formula using a calculator.
Cons:
- the formula is quite complex to memorize.
- Quadratic formula can be difficult to work with especially for someone who is finding it difficult to understand math.
Graphing method: the quadratic equation is been graphed on a coordinate pane and to get the accurate solution to the problem, the x-intercepts must be found.
Pros:
- it is easier to find x-intercepts on the graph.
- This method makes it easier to visualize the quadratic equation.
Cons:
- if the graph lack precision the final result might be inaccurate.
- It can consume lots of time especially when handling large coefficients.
TASK 3
Solve for linear equation 3x + 2 = 11 and show the value of x?

Sove for this quadratic equation x^2 + 2x – 6= 0
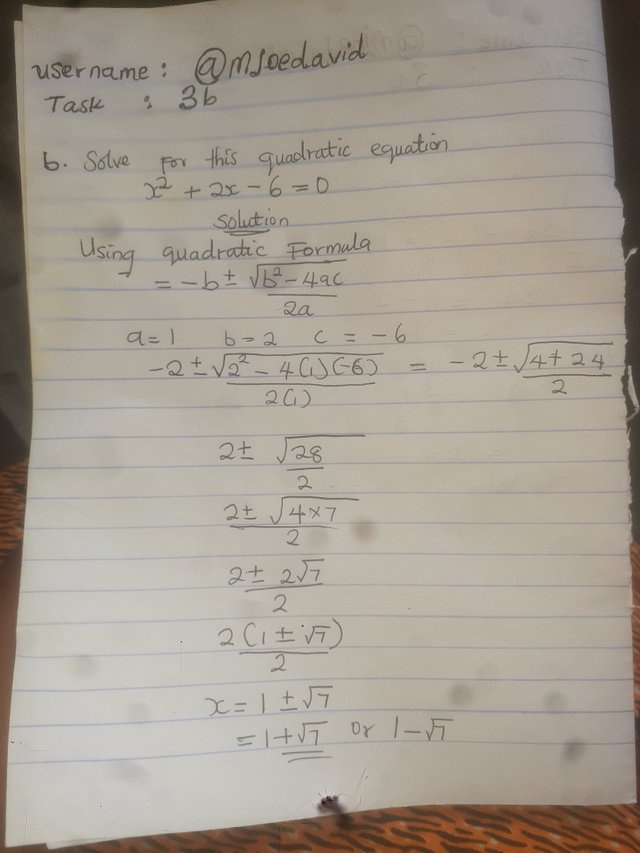
TASK 4
SCENARIO 1
Suppose Ali have $15 for spending at snacks. He is buying a pack of chips for $3. How much money does he have left?
Suppose x is amount of money Ali has left.
Equation: x + 3 = 15
Share a solution for x

SCENARIO 2
Suppose there’s a ball which is thrown in upward direction from ground with initial velocity of 20 m/s and height of ball above ground is presented by following equation; h(t) = -5t^2 + 20t
Here h is height in meters and t is time in seconds.
Share about maximum height reached by this ball
Solve for h

@khursheedanwar Thanks a lot you are a good tutor.