 |
|---|
Greetings everyone and welcome to my publication on Variables and Expressions as journey through the season of Algebra. And as we journey through, I hope you get to learn a thing or two too.
Explain any two variables and expressions types other than that which are explained in this course. |
|---|
Generally in english a variable is any symbol or letter that represents a value that can change or vary over time. They act as placeholders or symbols that represent unknown values were we can think of them as boxes that can hold different numbers. For example, if we have a variable like "x," it can stand for any number we want.
Expressions on the other hand are the combining of numbers, variables (unknowns), and operations (like addition, subtraction, multiplication, and division) and they act as phrases in mathematics to show the relationship between numbers and variables. For example, the expression "2x + 3" means "twice the value of x plus three."
In mathematical terms, variables specifically represent quantities that can change or vary, It's often used in mathematics and science to create general statements or formulas that can apply to many different situations. while expressions are mathematical statements that combine these variables and numbers using mathematical operations we know such as addition (+), subtraction (-), division (➗), multiplication (x) etc.
TYPES OF VARIABLES
Other than the types of variables discussed in class which are dependent and independent variables, there are also several variables of which include;
Controlled Variables:
These are variables that we keep constant throughout an experiment to ensure that any changes in the dependent variable are solely due to the independent variable. For example, if we are studying the effect of study time on the test scores of students, we can control the type of study materials used the students will use, the environment in which they will study, and the time of day when they can study. Then this is known as control variables.
Categorical Variables:
These are variables that can be divided into groups or categories that do not have a numerical value. For example, if we categorize students based on their preferred learning style such as visual learners or auditory learners. We are doing what is known as a categorical variable.
TYPES OF EXPRESSIONS
Just like with the types of variables, same applies to the expressions discussed in class which are numerical and algebraic expressions, there are other mathematical expression which include;
Logical Expressions:
These types of expressions involve logical statements that have to be either true or false. For example, if we say "5 is greater than 3," it is considered as a logical expression because it can be evaluated as true. However in mathematics, logical expressions use symbols such as AND, OR, and NOT to combine these different statements.
For example, "It is raining outside AND it is cold". This is a logical expression that is only true if both conditions are true.
Set Expressions:
This type of mathematical expression deals with the collection of objects or numbers into groups called sets. Where a set is represented by curly braces.
For example, the set of even numbers can be expressed as {2, 4, 6, 8, ...}.
In this type of expression, we also use set notation to describe the relationships between two or more sets.
For example, "A ∩ B" means the intersection (meeting point) of sets A and B, or the elements that are common to both sets. Therefore, Set expressions help us to organize and understand groups of items.
Show your way of evaluating of an algebraic expression if values of variables are given? Step by step explanation required |
|---|
In this part of the world, from childhood we are taught to evaluate all mathematical expressions using BODMAS, which is an acronym for BRACKET, ORDER, DIVISION, MULTIPLICATION, ADDITION and SUBTRACTION just like PEDMAS I have come to learn of from this week's lesson, and here is what each part means:
Brackets:
First, we are to solve anything inside brackets or parentheses. For example, in the expression (3 + 2) × 4, we would first calculate what is inside the brackets, which is 5.
Orders:
This refers to powers or exponents, and it means that after solving brackets powers or exponentials comes second. For instance, in the expression 2², we would calculate 2 raised to the power of 2, which equals 4.
Division and Multiplication:
These operations are of equal priority and should be solved from left to right. So, if we have an expression such as 8 ÷ 2 × 3, we would first divide 8 by 2 to get 4, and then multiply by 3 to get 12.
Addition and Subtraction:
Like the division and multiplication, these are also of equal priority and should be solved from left to right. For example, in the expression 5 + 3 - 2, we would first add 5 and 3 to get 8, and then subtract 2 to get 6.
Hence, we can see that PEDMAS is similar to BODMAS but uses the word "Parentheses" instead of "Brackets" and "Exponents" instead of "Orders".
Now with that in mind, let's go through a step-by-step way of evaluating an algebraic expression using specific values for the variables. I will be using a simple expression as an example:
Let's say we have the expression: 2x + 3y - 4. where x = 5 and y = 2
Here is how I would evaluate the expression step by step:
First, identify the Expression, as we have the expression 2x + 3y - 4. Where X and Y are 5 and 2 respective. Then,
Substitute the Values:
Since the variables x and y are given values, we replace the variables (x and y) with the values given. So, we replace x with 5 and y with 2, which will give us;
- 2(5) + 3(2) - 4.
Perform the Multiplication:
Now following BODMAS, we need to calculate the brackets part first by multiplying what's to the left of the bracket to the bracket as shown below:
- 2(5) = 10,
- 3(2) = 6.
Therefore, the expression now looks like this:
- 10 + 6 - 4.
Perform the Addition:
Next is for us to carry out the addition and subtraction part but following from left to right, therefore we have;
- 10 + 6 = 16.
To give us the expression; 16 - 4.
Perform the Subtraction:
Finally, we can now subtract to get the final answer as;
- 16 - 4 = 12.
So, after evaluating the expression 2x + 3y - 4 with the values x = 5 and y = 2, we find that the final answer is 12.
Simplify this expression: 3(2x - 1) + 2(x + 4) - 5. Evaluate this expression: (x^2 + 2x - 3) / (x + 1) when x = 2. AND Solve the following equation: 2x + 5 = 3(x - 2) + 1 |
|---|
FIRST SCENARIO
 |
|---|
Starting with the original expression:
- 3(2x - 1) + 2(x + 4) - 5
I will be Applying the BODMAS rule, which says that, we first deal with brackets. Therefore we need to distribute the numbers outside the brackets to the terms inside.
Distribute in the first term:
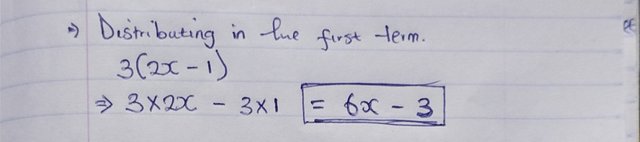
So, this becomes:
- 6x - 3
Distribute in the second term:
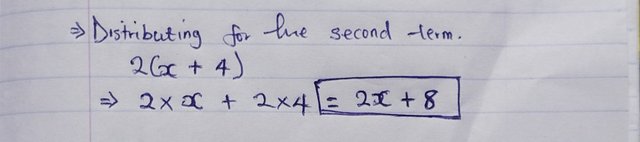
This becomes:
- 2x + 8
Combine all parts of the expression:
Now, we can rewrite the entire expression with the distributed terms as;
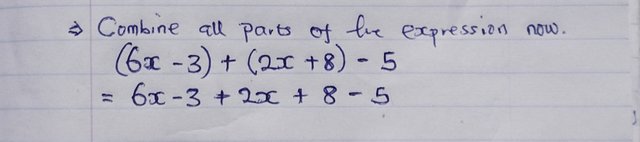
Which gives us,
- (6x - 3) + (2x + 8) - 5
- 6x - 3 + 2x + 8 - 5
Collect like terms:
This means that we can now combine all the x terms one side and the constant terms one side as shown below and solve.
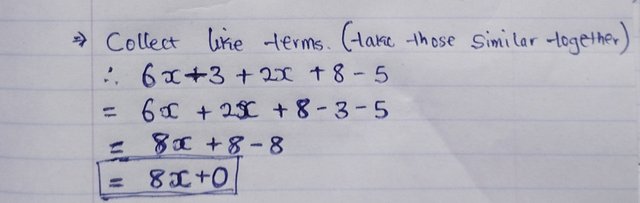
Where,
- 6x + 2x = 8x, and
- 8 - 3 - 5 = 8 - 8 = 0
Giving us;
- 6x + 2x + 8 - 3 - 5
as, - 8x + 8 - 8
- 8x + 0
Therefore, the expression simplifies to:
- 8x + 0
Therefore the final answer of the simplified expression is 8x.
SECOND SCENARIO
 |
|---|
To evaluate the expression (x^2 + 2x - 3) / (x + 1) when x = 2, follow these steps:
From the expression, we can see that there is an exponential or order or power, any we use. Meaning we are to deal with that first. But then, before we can go on, we need to substitute the value of "x" which is given as "2" into the expression.
Substitute 2 for x in the expression:
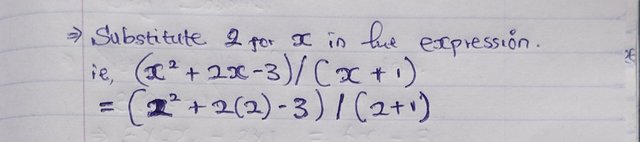
Now, we calculate the numerator. I.e., all the terms that comes before the division sign.
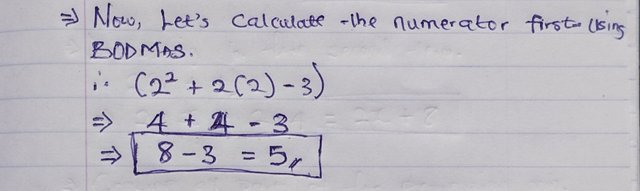
Where,
- 2^2 = 4
- 2(2) = 4
So, the numerator becomes:
- 4 + 4 - 3
- 8 - 3 = 5
Now, let's calculate the denominator. That is, any term that comes after the division sign.
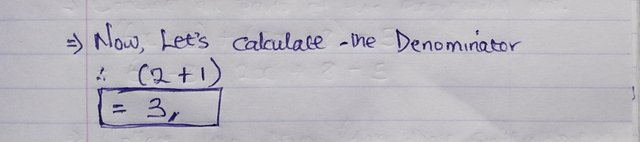
Which is;
- 2 + 1 = 3
Next we have both the denominator and the numerator solved, next is to put them all together as it was in the expression.

Which gives us;
- 5 / 3
So therefore, the final answer is 5/3.
THIRD SCENARIO

Let's solve the equation 2x + 5 = 3(x - 2) + 1 step by step:
Now in the expression above, we have an equal sign which separates our terms, hence giving us a Right Hand Side (RSH) and a Left Hand Side (LHS).
Where:
LHS = 2x + 5
RHS = 3(x - 2) + 1
Since the RHS has a brace, and using BODMAS, brackets comes first, we first need to distribute on the RHS.
So we start by distributing the 3 into (x - 2):
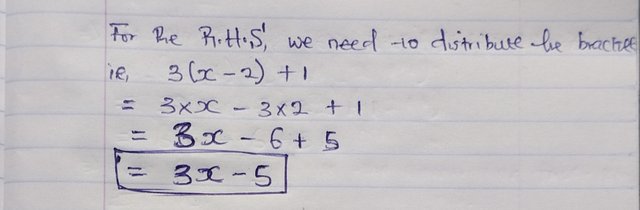
- 3(x - 2) + 1 = 3x - 6 + 1
Which gives us; - 3x - 5
Now we have simplified the RHS, so we can now combine it the to original expression to give us;
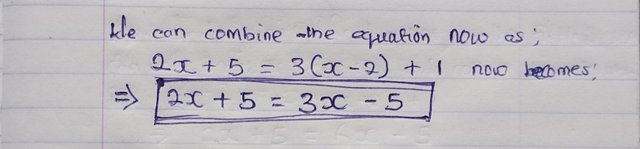
- 2x + 5 = 3x - 5
To solve for x, let's move all terms involving x to one side and constant terms to the other side in what we call collecting like terms. However we need to pay attention to the mathematical signs infront of the terms, because as they become the opposite. That is, if a negative (-) sign crosses the equal to sign, it becomes positive (+) and if a positive (+) sign crosses the equal to sign, it becomes negative (-).
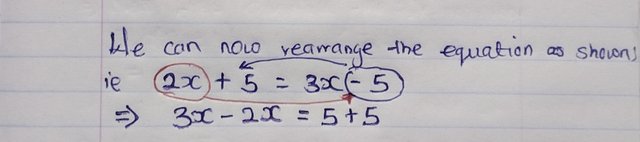
Hence, we now have.
- 3x - 2x = 5 + 5
Solving this gives us;
- x = 10
So, the solution to the equation is x = 10.
Task no.4 |
|---|
(a.) Suppose there's a bakery selling a total of 250 loaves of bread per day. They are selling whole wheat and white bread loaves with numbers of whole wheat loaves sold being 30 more than the number of white bread loaves.
To write an expression representing the bakery's total daily profit, let us break down the information given:
And to do that, Let's say "x" is the number of white bread loaves sold.
Therefore,
- White bread = X
And again, since the number of whole wheat loaves sold is 30 more than the number of white bread loaves, then the number of whole wheat loaves sold can be expressed as X + 30.
i.e,
- Wheat loaves = X + 30
But then, the total number of loaves sold is 250. Therefore, we can write the equation as;
| X (white loaves) + (x + 30) (whole wheat loaves) = 250 |
|---|
Now, we can simplify this equation as shown below;
- X + X + 30 = 250
- 2X + 30 = 250
- 2X = 250 - 30
- 2X = 220
- X = 110.
Therefore, the total number of white bread loaves sold is 110. Since;
White bread = X, and X = 110, therefore;
- White loaves = 110
Then, substituting 110 into the equation, Wheat loaves = X + 30, we can then find the number of whole wheat loaves sold has;
- Wheat loaves = X + 30, where X = 110,
i.e., - X + 30 = 110 + 30 = 140.
Therefore, the total number of Wheat bread loaves sold is 140.
Next, we can now calculate the profit:
From the question, the profit from white bread loaves is $0.50 per loaf, so for X white loaves, the profit is 0.50 x X.
And since the profit from whole wheat loaves is $0.75 per loaf, so for (X + 30) whole wheat loaves, the profit is 0.75 x (X + 30).
Now, we can write the expression for the total daily profit as;
| Total Profit = Profit from white loaves + Profit from whole wheat loaves |
|---|
- Total Profit = 0.50 x X + 0.75 x (X + 30).
where X = 110
Therefore, substituting x = 110 into the expression gives us;
- Total Profit = 0.50 x 110 + 0.75 x (110 + 30)
- Total Profit = 0.50 x 110 + 0.75 x 140
- Total Profit = 55 + 105
- Total Profit = 160.
Therefore, the expression for the bakery's total daily profit is 0.50 x X + 0.75 x (X + 30), and the total profit is $160.
(b.) If x is representing number of white bread loaves sold out and bakery is making a profit of $0.50 for each white bread loaf and $0.75 for each whole wheat loaf then please write an expression for representing bakery total daily profit.
To write an expression for the total cost of renting the car for x hours, we need to consider two scenarios based on the number of hours rented.
For x hours less than or equal to 4, the cost is given by the expression 2x + 15. i.e., the expression from the question for daily rentage.
Then, for x hours greater than 4, the rental company offers a package deal, which costs 3x - 2.
Now, we can express the total cost based on the value of x:
i.e.,
- If x ≤ 4: Total Cost = 2x + 15. and,
- If x > 4: Total Cost = 3x - 2.
To simplify the expressions, we'll look at each case:
| Case 1: when x ≤ 4 |
|---|
- Total Cost = 2x + 15.
This is because the expression 2x + 15 is already simplified.
| Case 2: When x > 4 |
|---|
- Total Cost = 3x - 2.
This is also because the expression 3x - 2 is also already simplified.
Now, we have two expressions depending on the value of x:
Therefore to rent the car for 4 hours or less, the total cost is 2x + 15.
And, to rent the car for more than 4 hours, the total cost is 3x - 2.
This gives us a clear understanding of how the total cost varies based on the number of hours rented.
I want to take this opportunity to invite @bossj23, @ruthjoe and @ngoenyi.
Thank You for your Time
NOTE: Always have a smile on your face, as you are never fully dressed without one.
