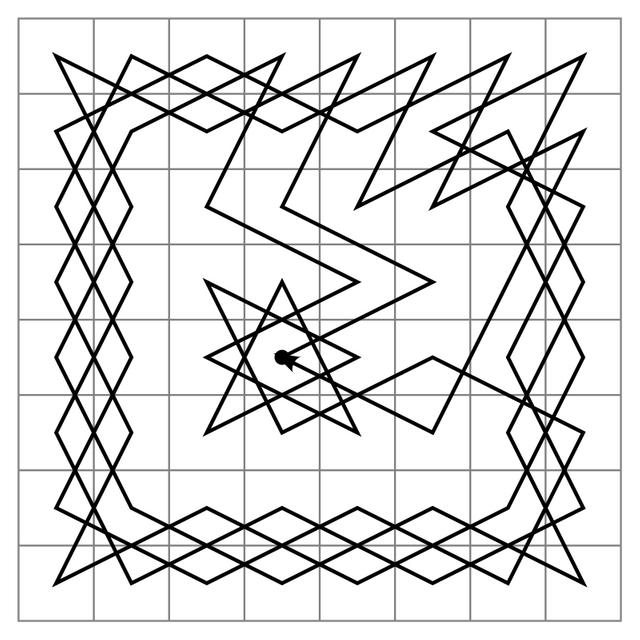
Chessboard is a square 8x8, with 64 points total. Did You know that it is possible for knigh to do a trip thourgh every point such that it visits every point exactly once? And there are many ways to do that. Above You have one opportunity. The first method was described in 1823.
Mathematical object "graph" can be though as a set of points (vertices) and set of lines connectign them (edges). Path between points is a trip from the start to the end, travelling through edges. Path which visits every point of the graph is called Hamiltonian path. If the start of the trip is also the end of the trip, we call it Hamiltonian cycle.
In general, it is not easy to check if a given graph has at least one Hamiltonian cycle. IF graph has n vertices, there is not known polynomial-time (on n) deterministic algorithm checking that for every graph.
Trip of our knight is exactly Hamiltonian path. The journey on the image is even Hamiltonian cycle, as D4 is both start and end of it. If someone will find such algorithm, he will obtain 1000000$ (which is extremely unfair in our world, because stupid celebrities get such money for a few posts on Instagram) and eternal fame.
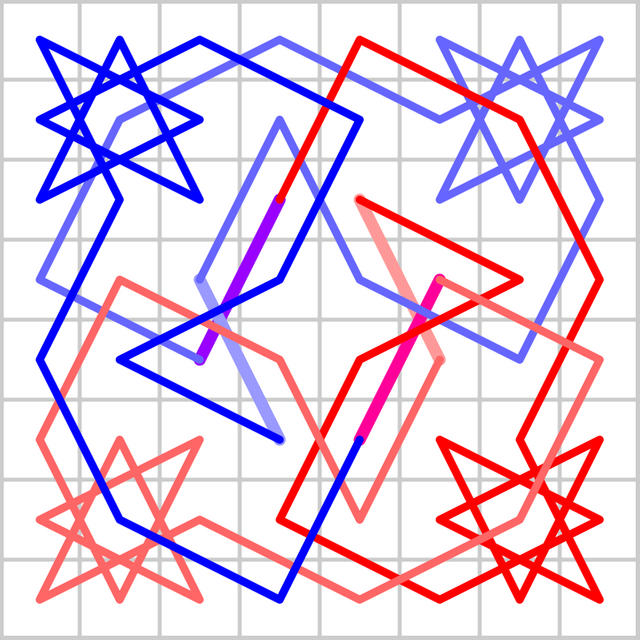
Here is another example.
Graph theory belongs to subjects of mathematics which I like to call "5 minutes to learn the rules, whole life to master." It may look easier for non-mathematicians at first when compared to hieroglyphs which are written on differential equations or algebraic topology, but it is not the case. Every branch of mathematics can be as hard as we want :)
Source of images:
https://en.wikipedia.org/wiki/Knight%27s_tour
A Very interesting graph of the knight moves. I am sure all the chess pieces will have an interesting graph.
My question: Who is paying the million dollars for the algorithm? (lol)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi. Thanks for Yur comment.
In 2000 7 mathematical problems for XXI century were chosen. Making solution for any of them is paid by Clay Mathematics Institute. However, Russian Gregorij Perelman who solved one in 2003, decided not to take money.
Finding deterministic algorithm running in polynomial time for Hamilton cycle (or proving it does not exist) answers first problem, popular "P vs NP".
Here is more:
https://en.wikipedia.org/wiki/Millennium_Prize_Problems
If You will have more questions I will answer tomorrow.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for that information about the Millennium Prize problems; it’s just as interesting as the graph.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks. I can write more now, I have cancelled exercises and lectures on studies until 14th April. Do You have any mathematical questions which You want me to write article about?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yes, as a matter of fact I wrote a chess program a few years ago, haven’t updated it though. And it was always my intention to find some way to use calculus (rate of change) equations to be a part of the chess engine. For many years I believe it could be done as oppose to ten or more iterations (loops). I’ve been lead to believe very early on that calculus could be applied to everything.
Can one apply calculus to a chess program?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hmm. I think that the future in computer in games is localised in machine learning. I think that it is too hard to measure precisely how arbitrary move will change the strengths. One different postiion of one figure can turn move which is at 1000 situations very good move into a very bad move. I think that chess are too complex to even write such equations, not saying about implementating them. Machine learning computers win in Chess, in Go, in Starcraft 2 easily with human. This is the future I think.
Maybe for checkers it would be possible, but it wouldnt be worth to do it I think.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for your reply and I agree.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute on May 24, 2000. The problems are the Birch and Swinnerton-Dyer conjecture, Hodge conjecture, Navier–Stokes existence and smoothness, P versus NP problem, Poincaré conjecture, Riemann hypothesis, and Yang–Mills existence and mass gap. A correct solution to any of the problems results in a US$1 million prize being awarded by the institute to the discoverer(s).
To date, the only Millennium Prize problem to have been solved is the Poincaré conjecture, which was solved in 2003 by the Russian mathematician Grigori Perelman, who declined the prize money.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit