In the previous lesson, we explored the basic elements of geometry: point, line, segment, ray, angle, perpendicular and parallel lines. We also covered vertical and adjacent angles, as well as angles formed by the intersection of two lines with a transversal. Additionally, we looked at how to construct them in GeoGebra. So, if anything here is still unfamiliar to you, please refer to the first lesson. You can also review the work of all participants from the previous lesson, especially kouba01, kafio, mojociocio

And in the second lesson, we will explore a more complex yet fundamental concept of geometry—the triangle.

Triangle

A triangle consists of three points...
If we take three arbitrary points A, B, and C that do not lie on the same line and connect them sequentially with segments—AB, BC, and AC—we obtain a figure called a triangle, specifically triangle ABC.

A triangle consists of three segments (sides).
However, if we take three arbitrary segments, it is not always possible to construct a triangle from them.
Sometimes, it may be necessary to draw a triangle using lines; in that case, the lines should be hidden while displaying only the triangle’s sides as segments. This will be useful later if the triangle is a derived figure, meaning it is formed as a result of constructing other figures.

The method of constructing a triangle depends on whether it is a primary figure or a derived one (a figure that results from another construction).

So, a triangle has three sides, three vertices, and three angles. But what other fundamental elements does a triangle have?

Altitude

An altitude is a perpendicular dropped from a vertex of the triangle to its base.

Let me remind you how to construct a perpendicular line:
You need to select the perpendicular line tool from the toolbar, specify the vertex from which the perpendicular is dropped, and then indicate the side to which the perpendicular line is drawn.

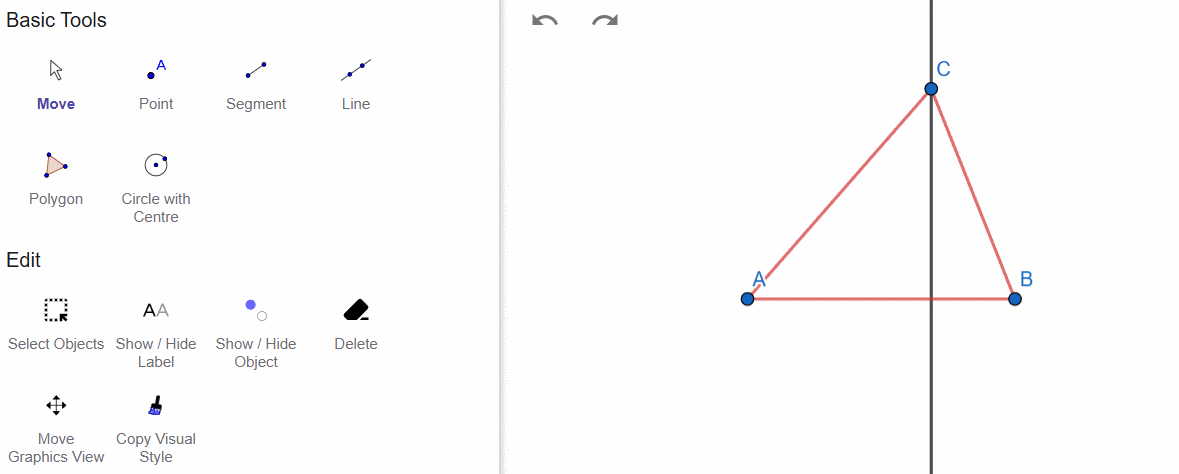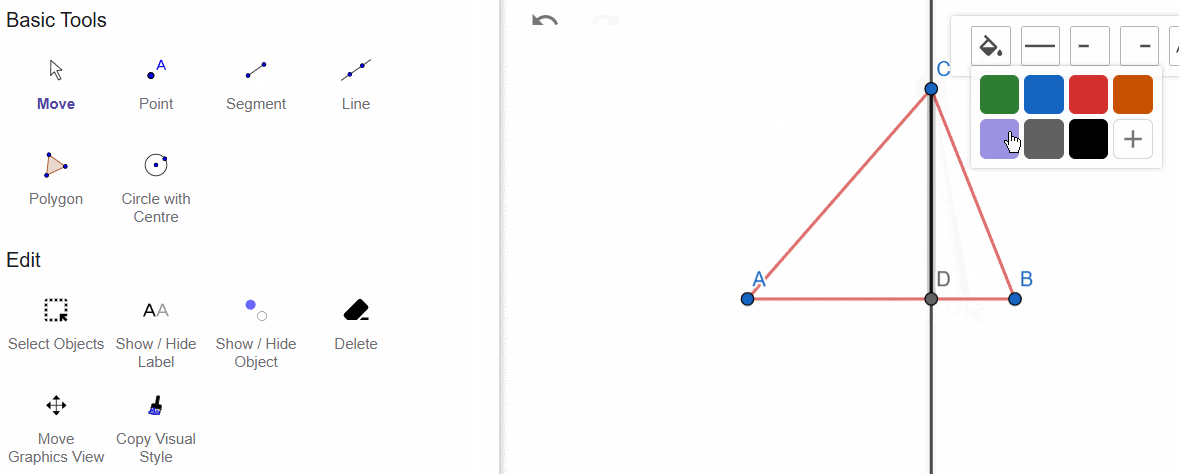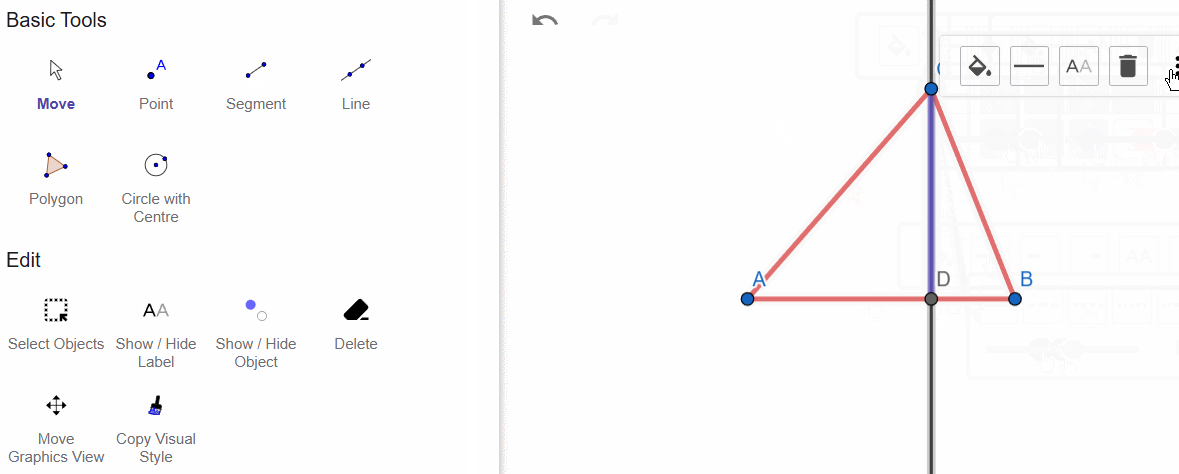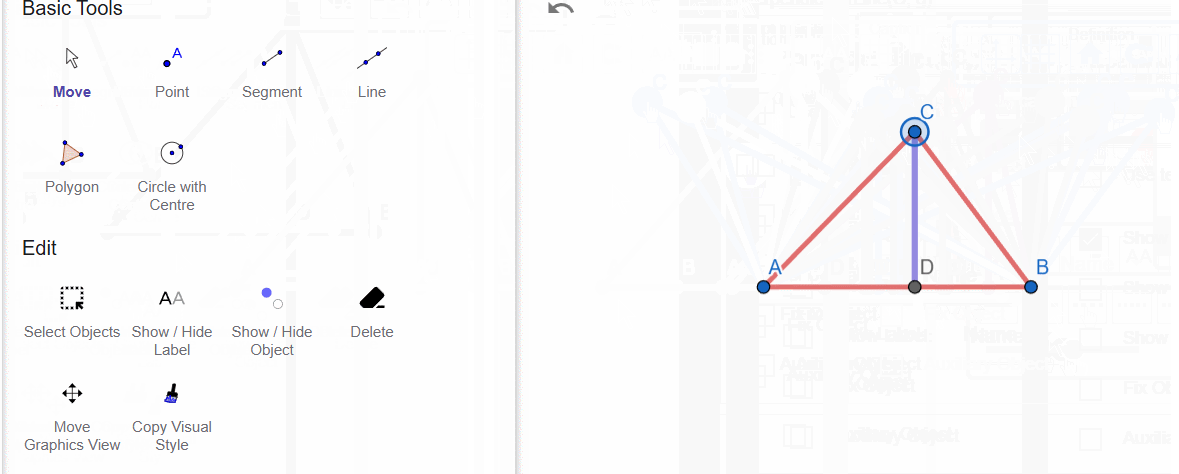
Here, I have dropped a perpendicular from vertex C to side AB.

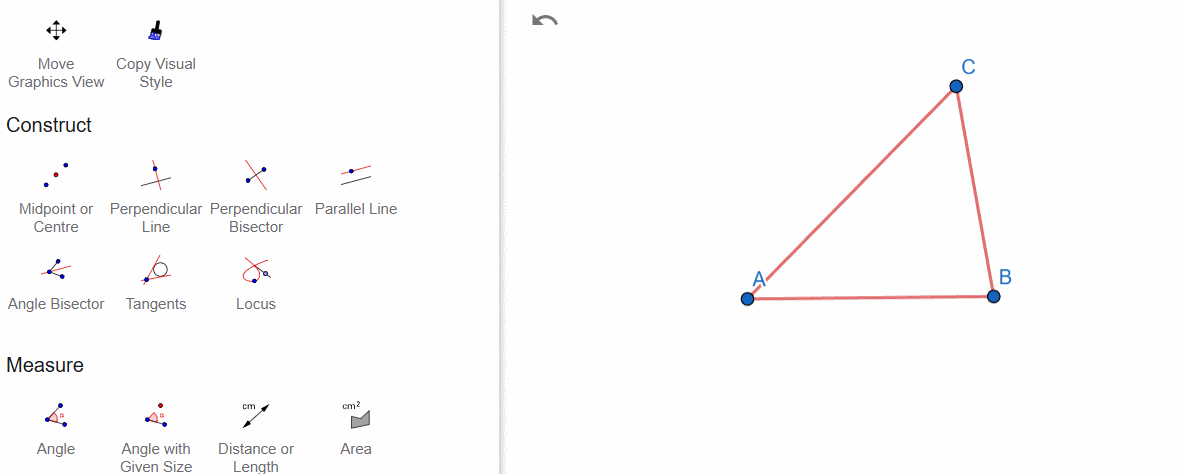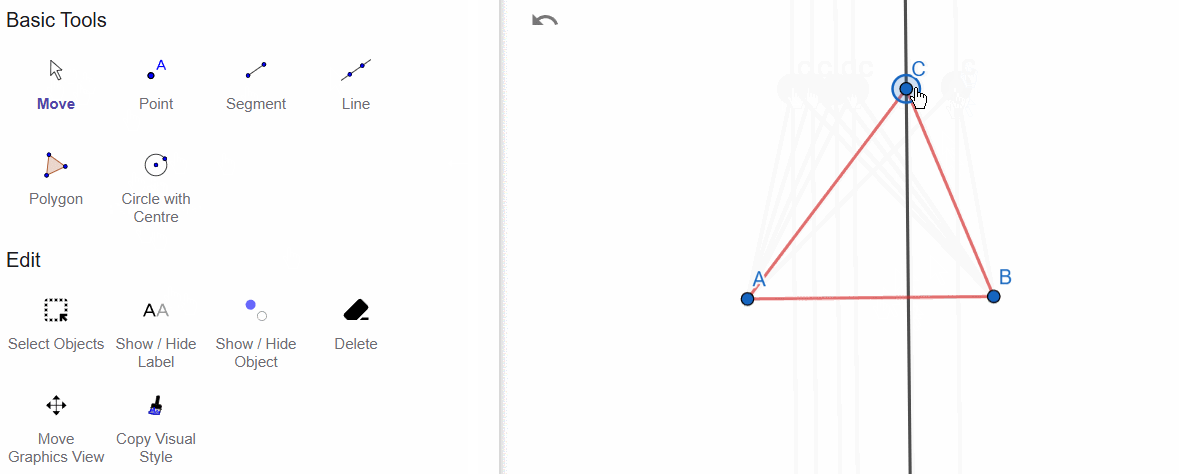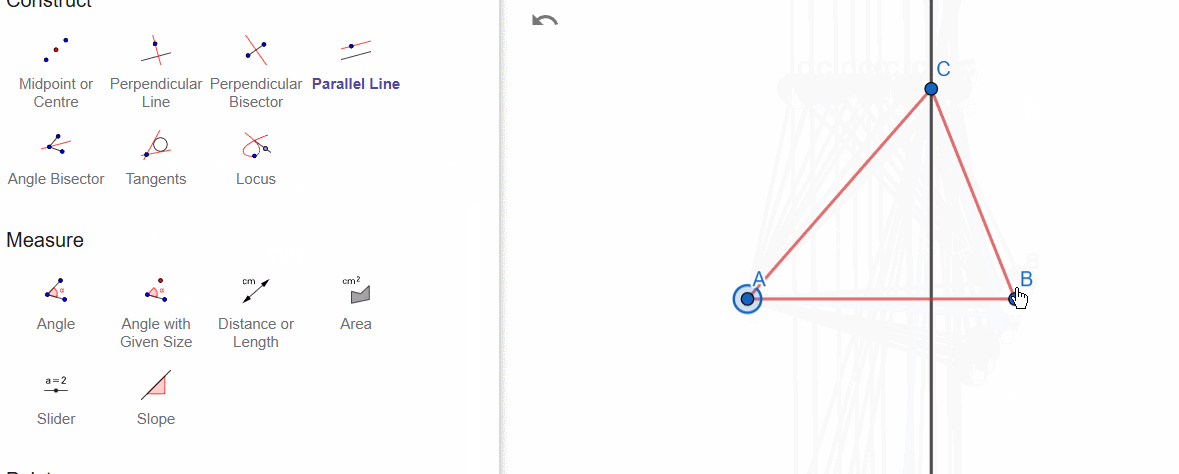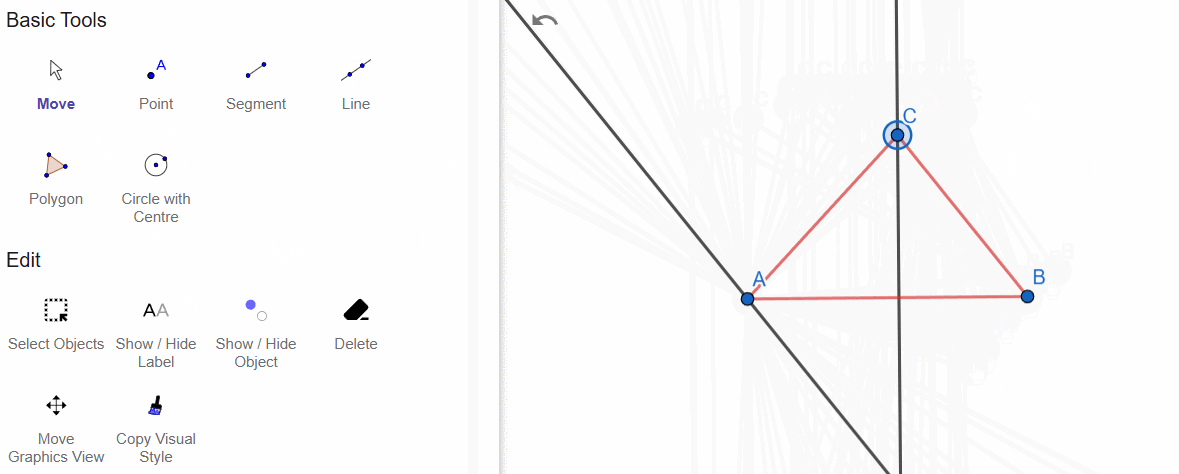
I also reminded here how to draw a line through vertex A that is parallel to BC.

Now, let’s construct the altitude of triangle ABC from vertex B.

The perpendicular line from point C to line AB is already drawn. Now, we need to construct the intersection point D. The constructed segment (perpendicular) CD is the altitude of triangle ABC, drawn from vertex C to side AB.

A triangle has a total of three altitudes since it has three vertices. From each vertex, only one altitude can be drawn to the opposite side.

All altitudes (or their extensions) intersect at a single point called the orthocenter.

Perpendicular Bisector (Mediatrix)

I'm not sure if you've heard this term before. When I was in school, I hadn't, but while flipping through an old math book, I noticed that what we were taught as the perpendicular bisector was called by a single word—mediatrix.

A mediatrix, or perpendicular bisector, is a perpendicular line drawn through the midpoint of a side.

Interestingly, the three mediatrices of a triangle also intersect at a single point.

The intersection point of the perpendicular bisectors is the circumcenter, which is the center of the circumscribed circle around the triangle.

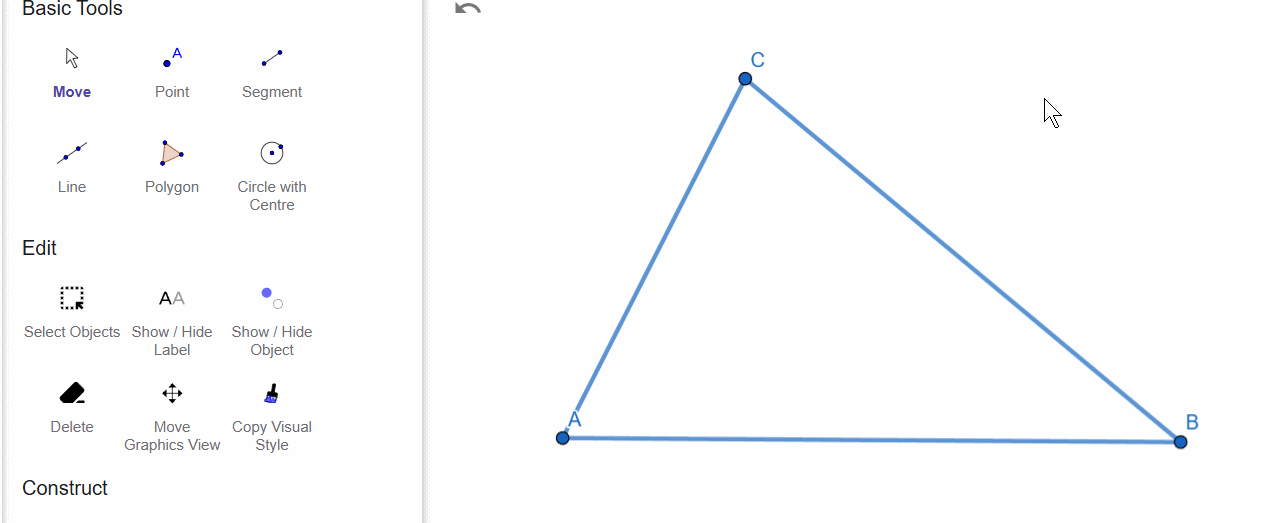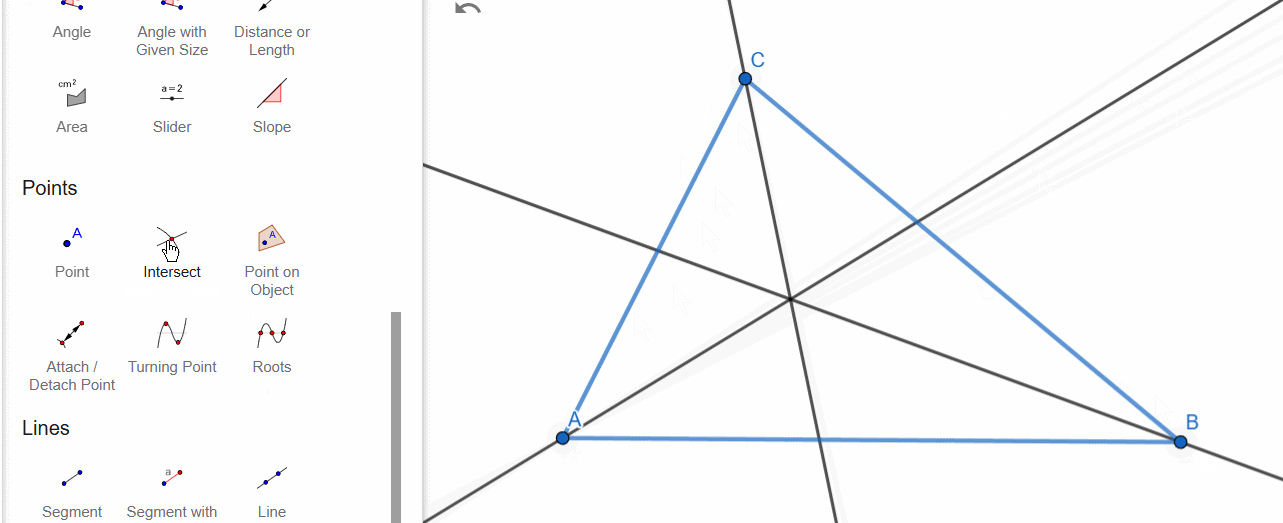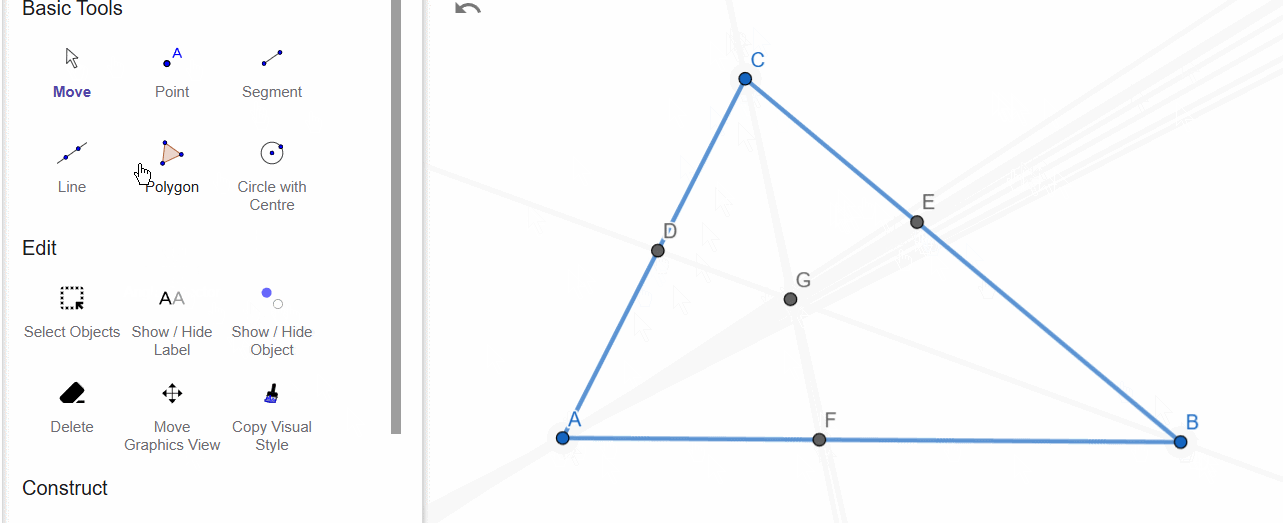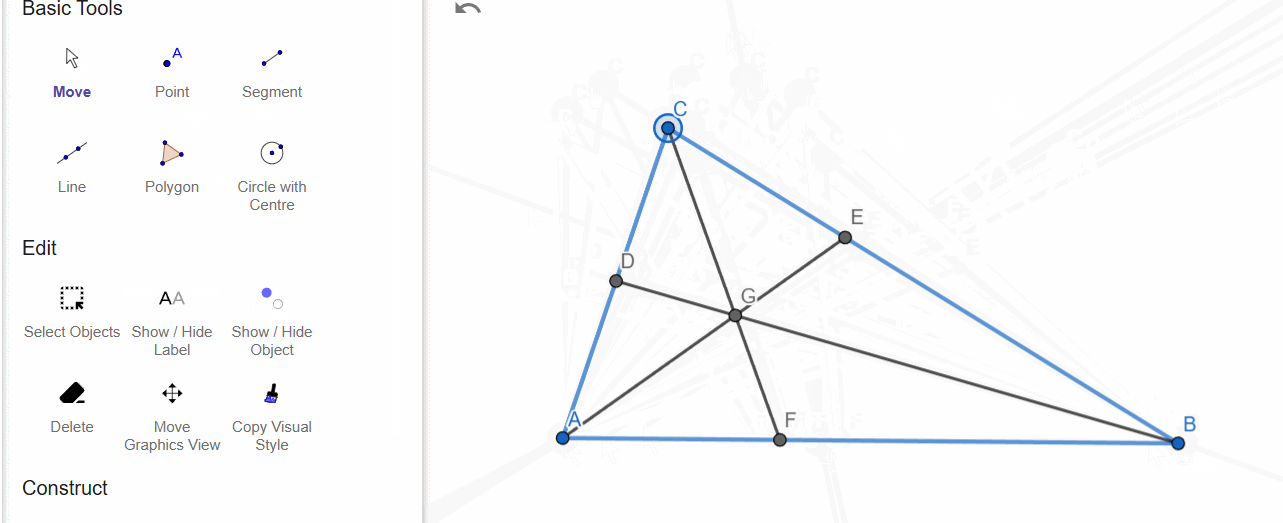
Median

A median is a segment that connects a vertex with the midpoint of the opposite side. The perpendicular bisector is only needed here to determine the midpoint of the side.

The medians of a triangle intersect and divide in a 1:2 ratio.

The point where the medians intersect is called the centroid, which represents the center of mass of the triangle.

A median divides the triangle into two equal-area triangles.

Angle Bisector

A median divides a side in half, while an angle bisector divides an angle in half.

The three angle bisectors of a triangle also intersect at a single point, which is the incenter—the center of the inscribed circle within the triangle.

Outline and Figure

A triangle can be viewed as three segments forming its sides or as a plane figure filling the area inside.

There is also another useful tool—a point on an object, which allows placing a point anywhere along a segment or inside the figure.

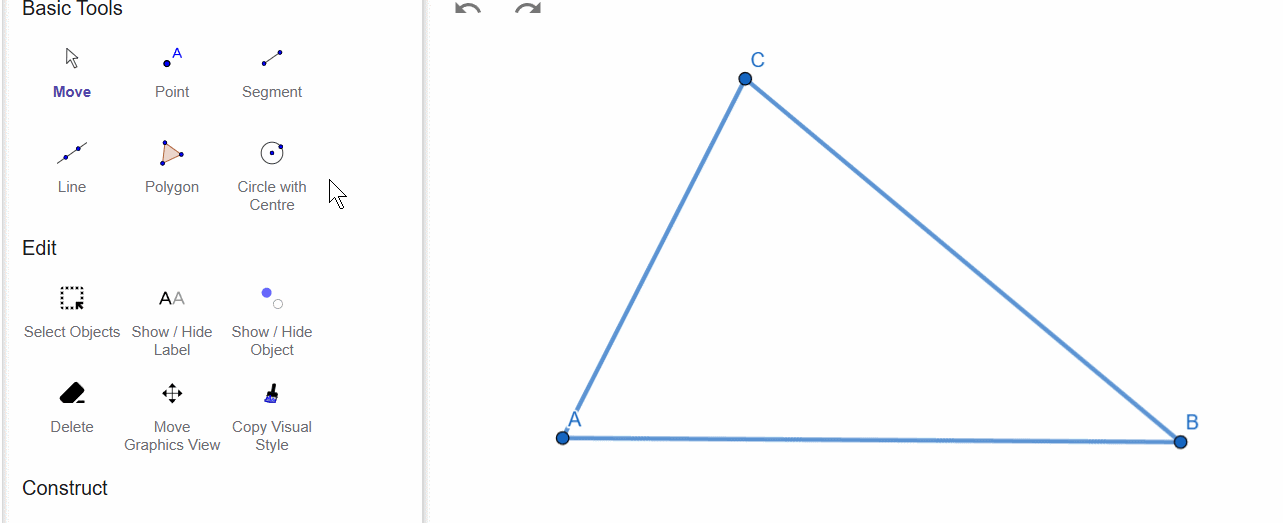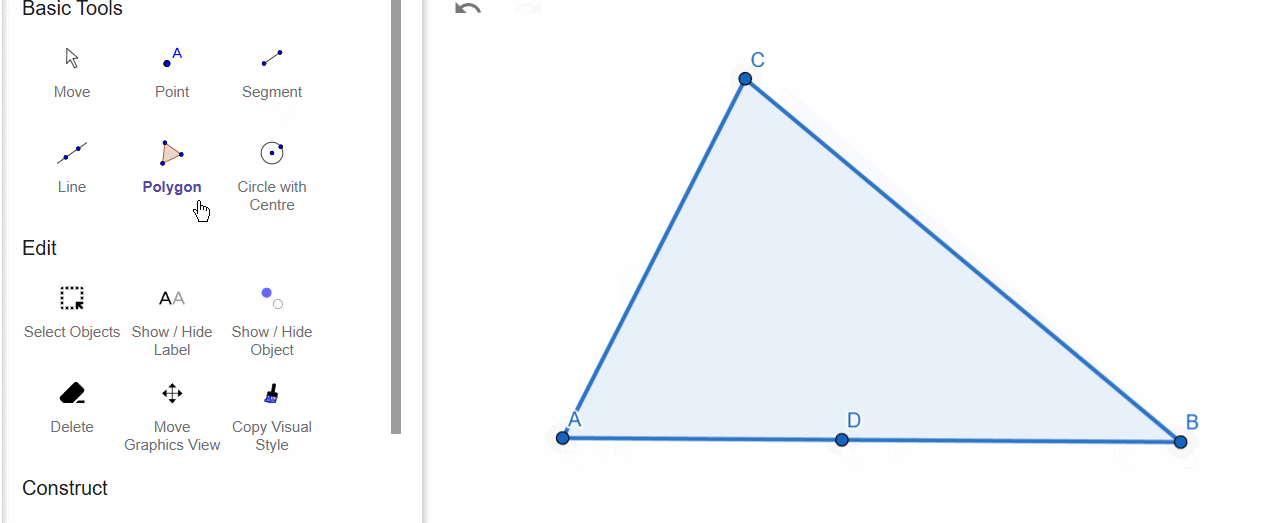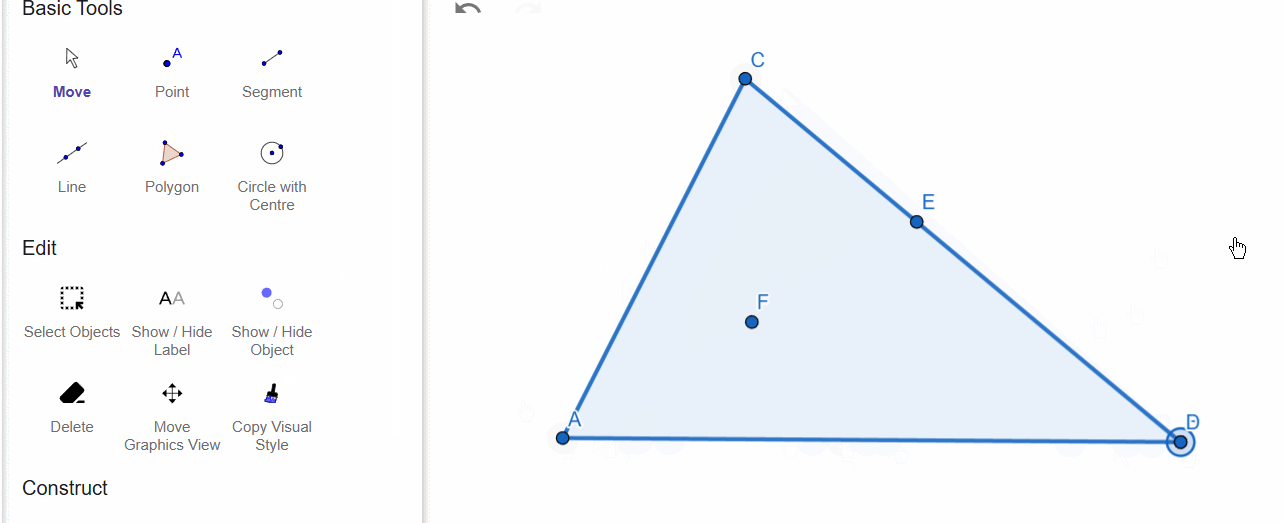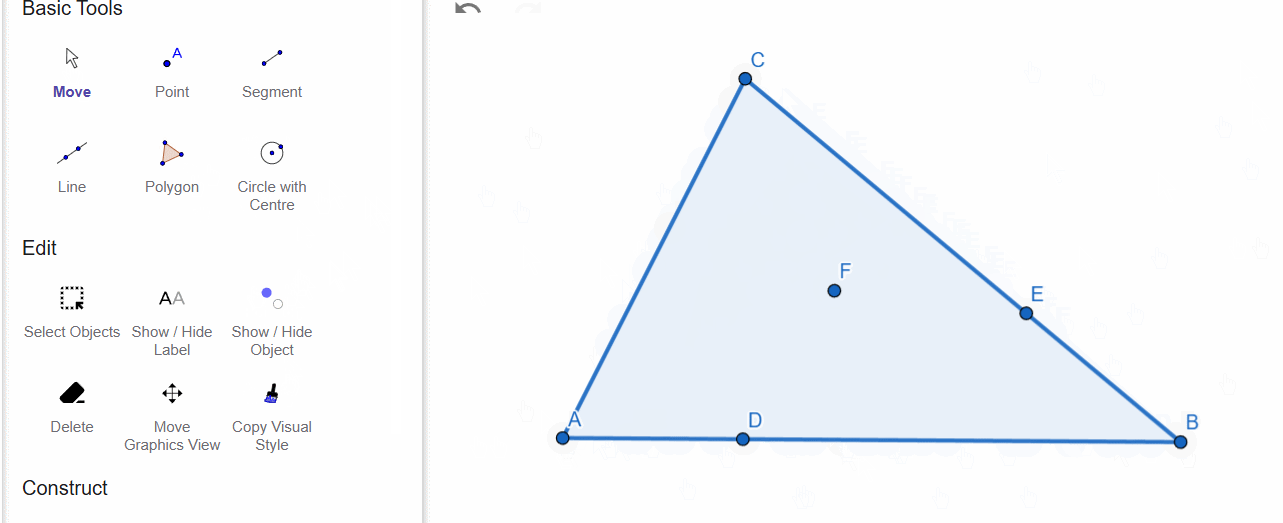
We will place point D on side AB. As you can see, the point can only be moved along this side.

Next, we will use the Polygon tool to create a plane figure—a triangle. If we now use the Point on Object tool and place a point on a side of the triangle, the point will slide only along the triangle’s sides.

However, if we place the point inside the triangle, it will move only within the plane of the triangle and will not go beyond its boundaries.

If all three sides of a triangle are equal, it is called an equilateral or regular triangle.
If only two sides are equal, it is called an isosceles triangle.

Homework Assignment

Tips

If you name a point H_1, it will be displayed as H₁.
If you name a side h_a, it will be displayed as hₐ.
If you're having trouble moving a point (it doesn't seem to move), it might be because you're selecting not a point but another object (such as a segment or line). To fix this, I solve it by assigning the point to a higher layer. This ensures it can be selected and moved properly.

Task1

Build a triangle with three altitudes.

When constructing the three altitudes, the point of intersection of the altitudes should always be displayed, as in task #5 (from the previous lesson), where the extensions of the altitudes to their intersection should be shown.

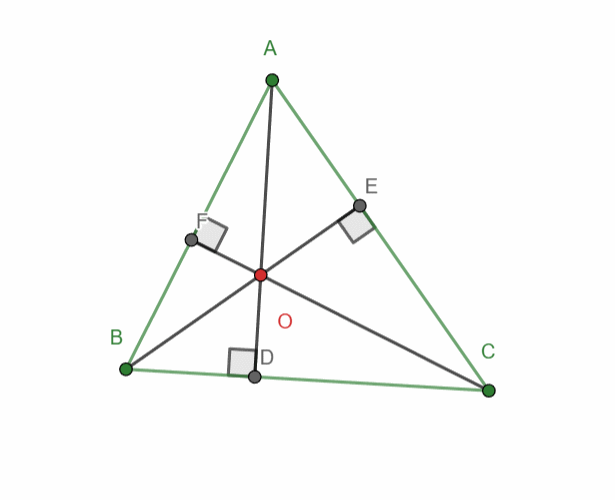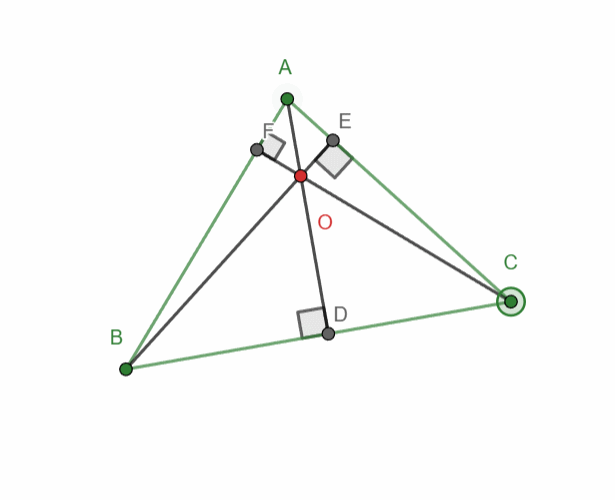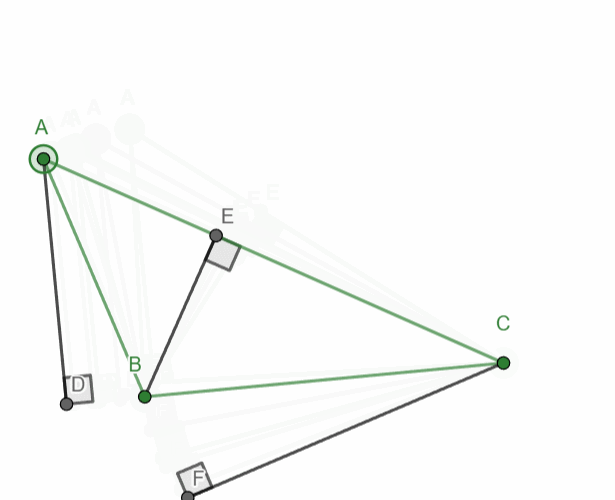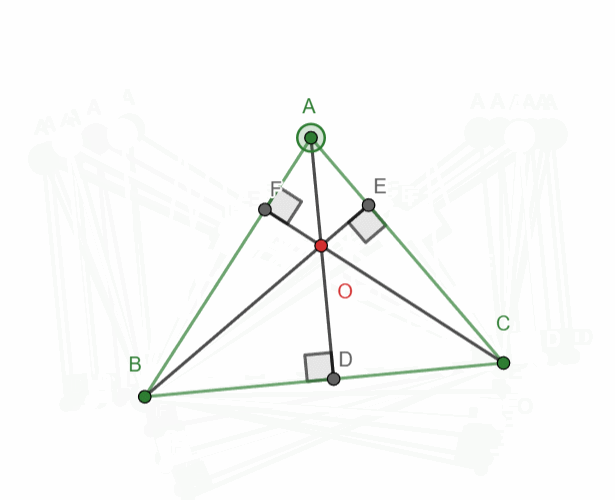
The animation shows half of the task completed. It should be done as shown in the image below. The altitudes must be displayed and also extended to the point of intersection.

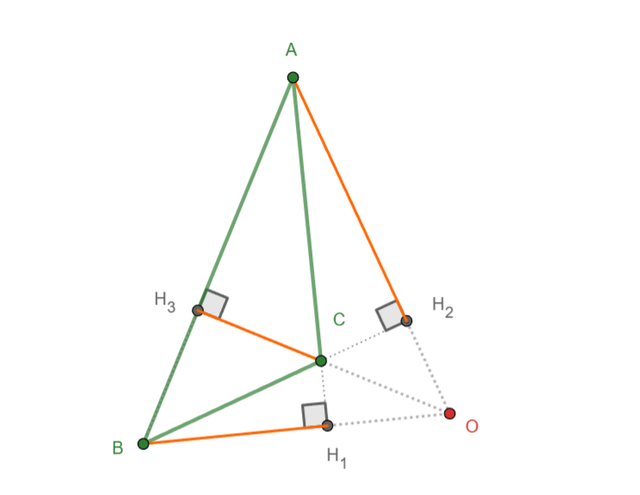
‼️You must construct and highlight all three altitudes of the triangle.

Task2

Build a triangle. From vertex A, construct (show) the altitude, angle bisector, and median.
Show that the altitude is a perpendicular line.
Show that the median divides the opposite side in half.
Show that the angle bisector divides the angle into two equal parts.
Make sure the altitude, median, and angle bisector stand out to draw attention to them.
‼️You must construct and show one altitude, one median, and one angle bisector from the same vertex.

Task 3

The Basics of Medians
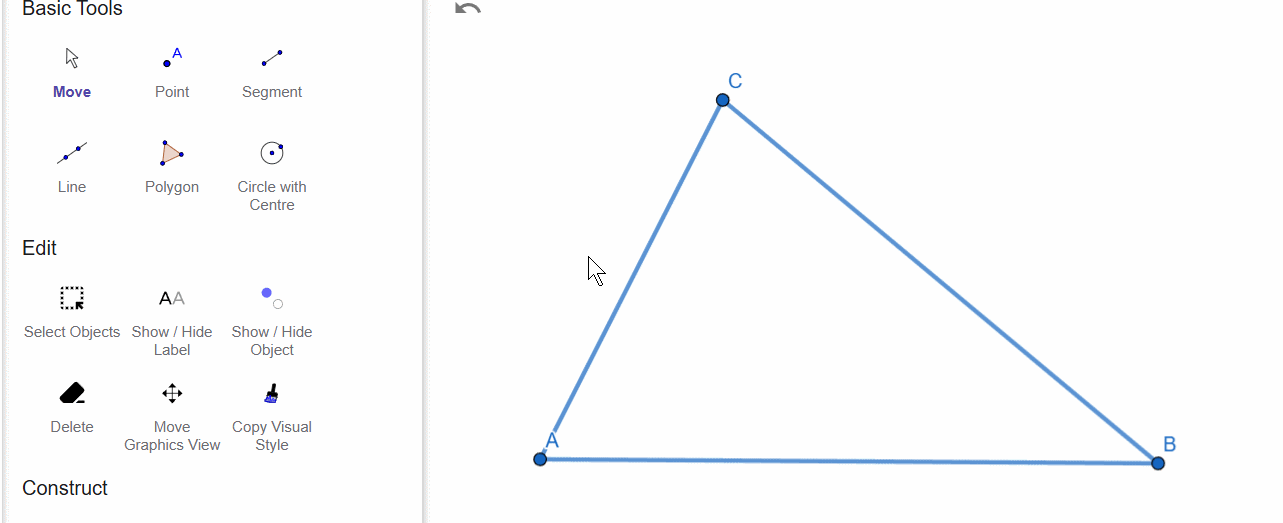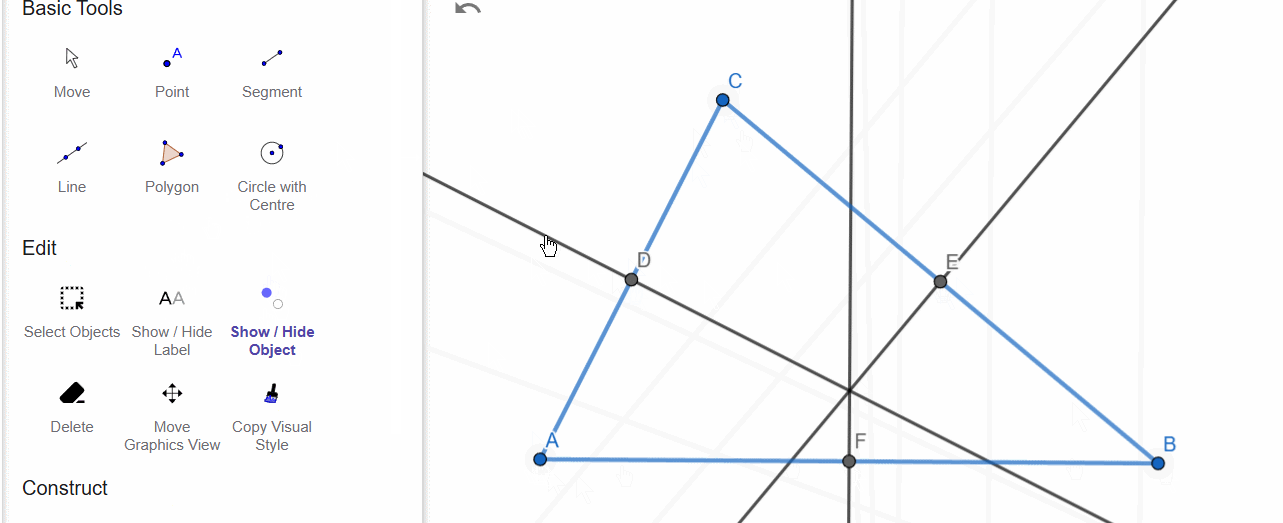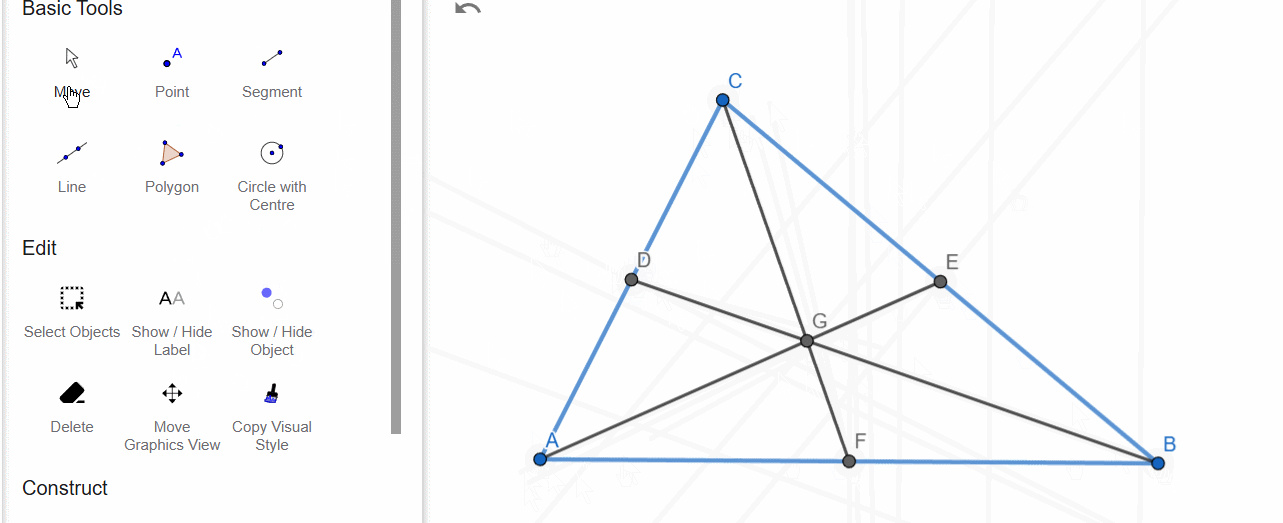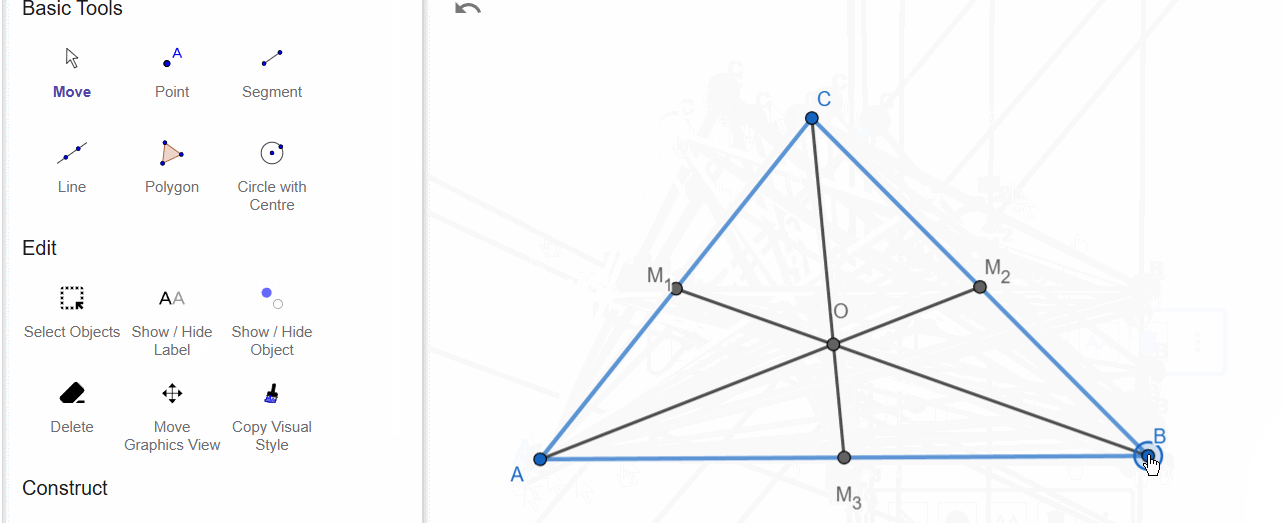
Build triangle ABC. Then, using the medians as the new triangle's vertices, construct a new triangle.

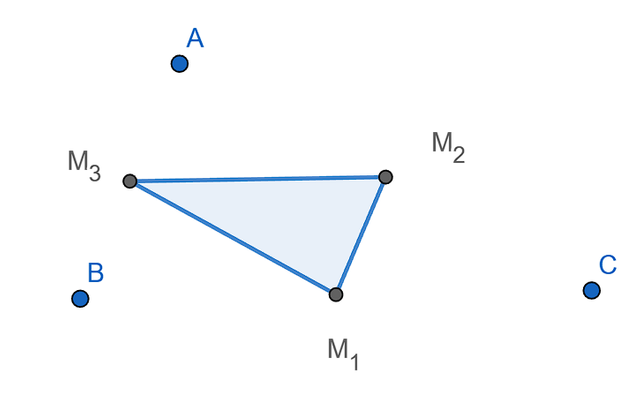
This triangle has several names: Medivan triangle, Ceva’s triangle, and Median triangle.
Construct triangle ABC, then build a new triangle M₁M₂M₃ using the midpoints of the medians as the vertices.
Hide the sides of triangle ABC, but display the halves of the sides and demonstrate that they are equal. (Use the Style/Decoration option to adjust the appearance.)

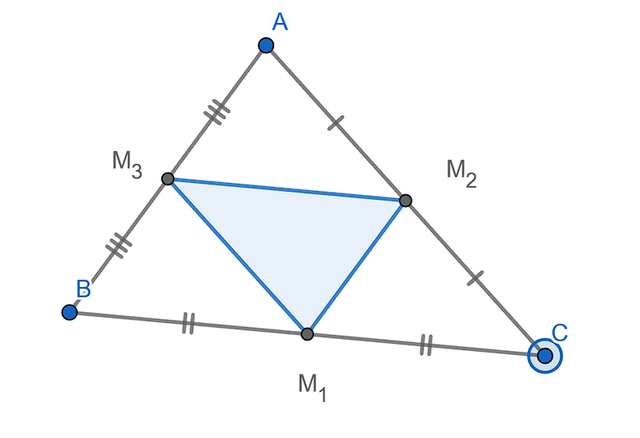
What properties does this triangle have?
‼️You must construct and show the median triangle – the triangle formed by the midpoints of the sides.

Task 4

The Bases of the Altitudes
Build triangle ABC, then, using the bases of the altitudes as the vertices, construct another triangle.

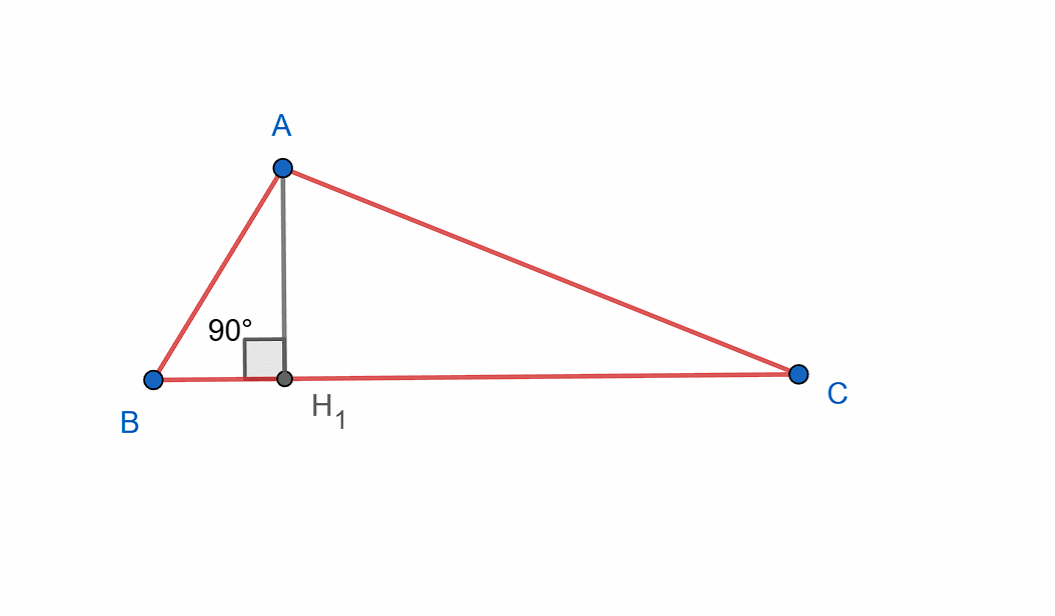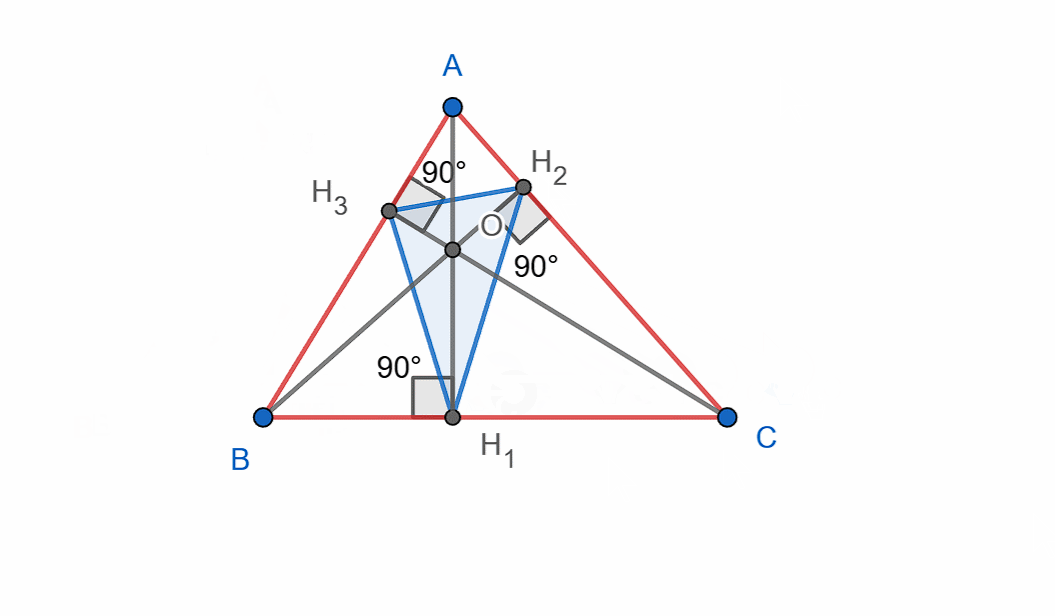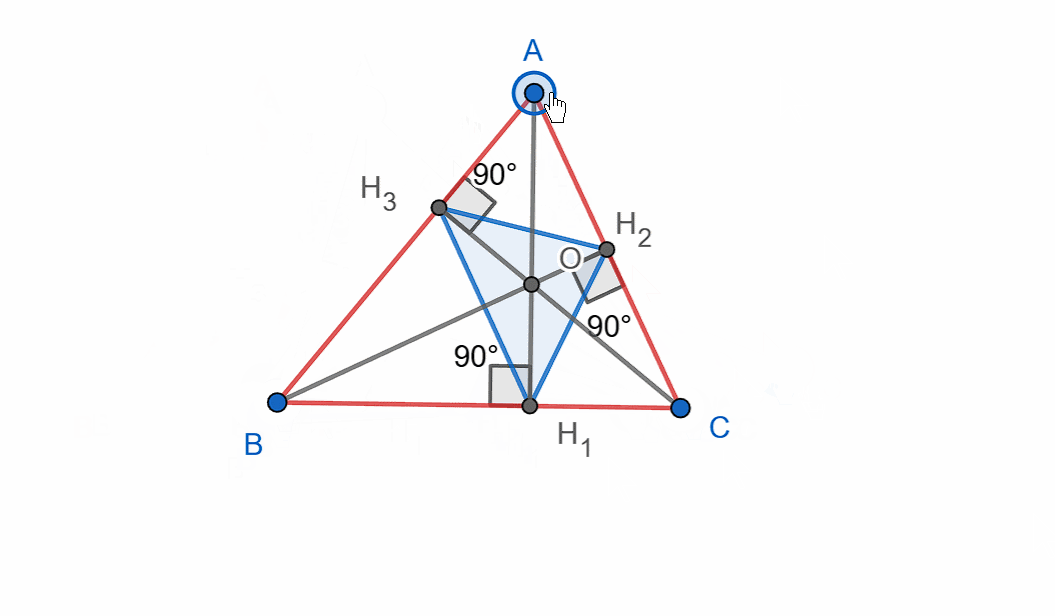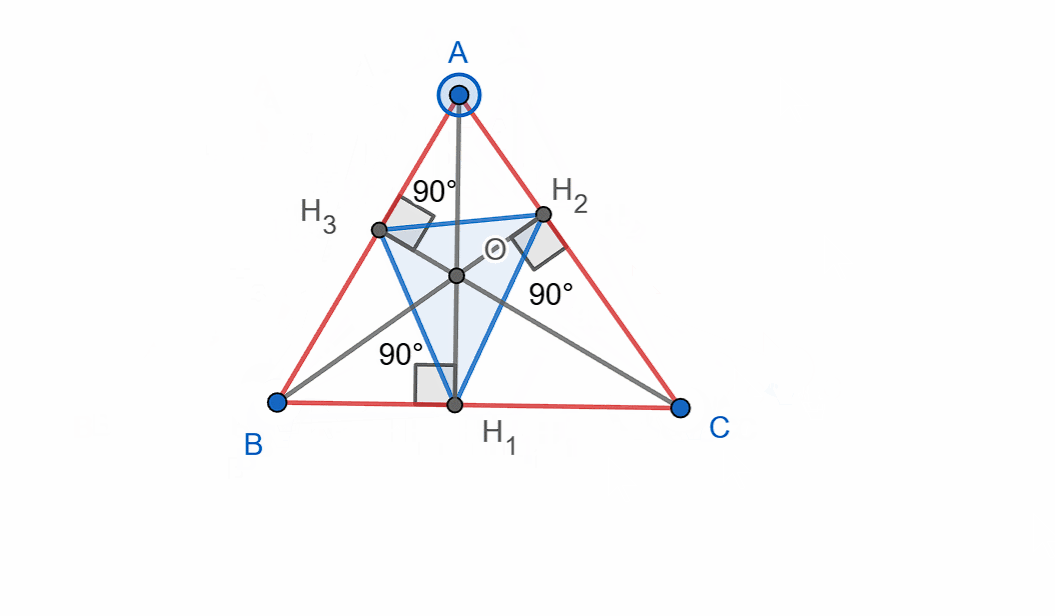
‼️You must construct and show the orthic triangle – the triangle formed by the feet of the altitudes.

Task 5

The Bases of the Angle Bisectors
Construct triangle ABC, then, using the bases of the angle bisectors as the vertices, construct another triangle.
Show that the angles formed are exactly the angle bisectors.

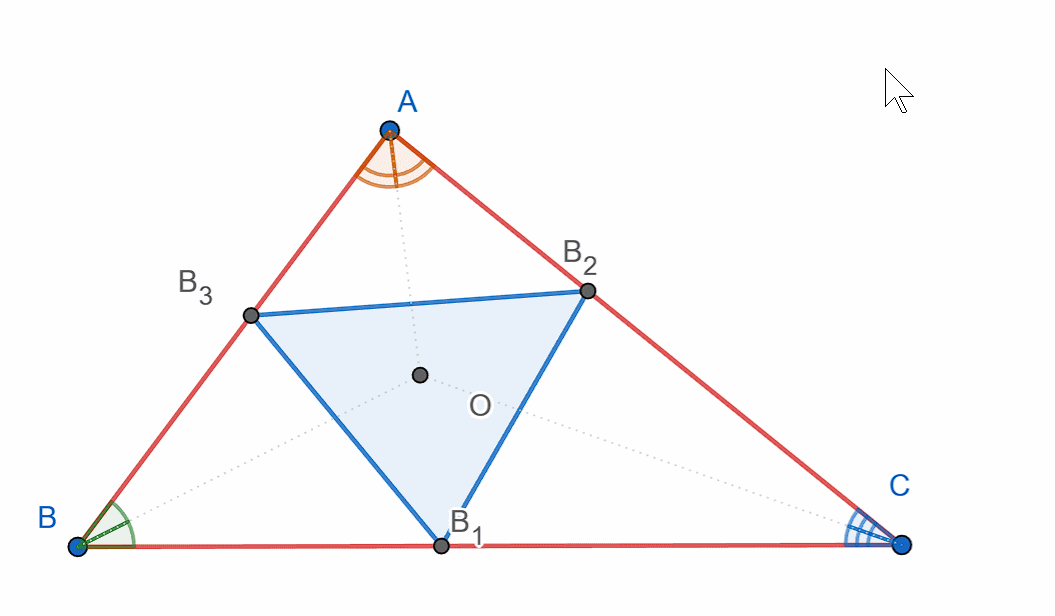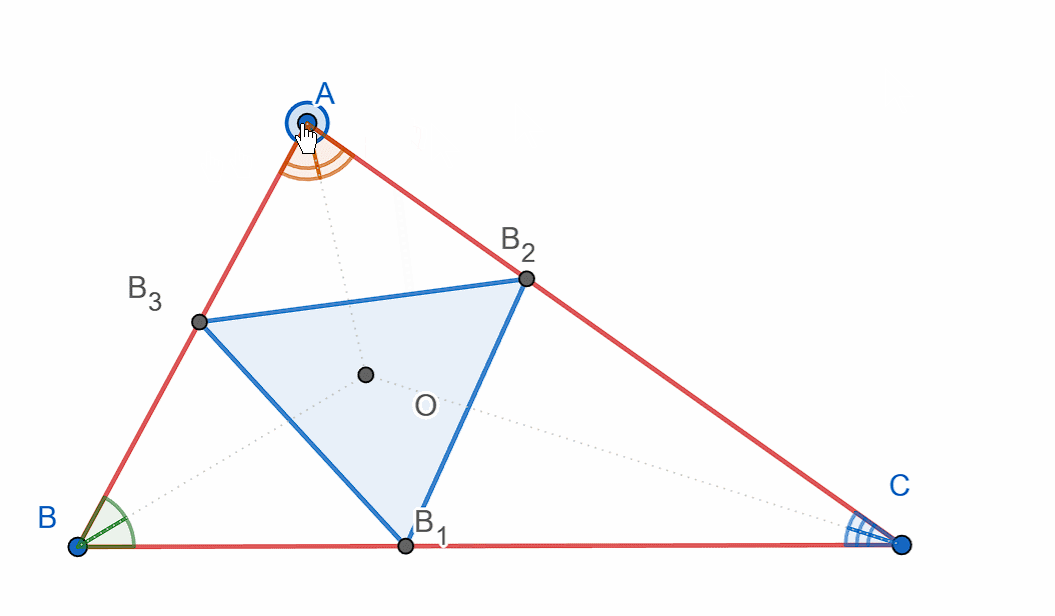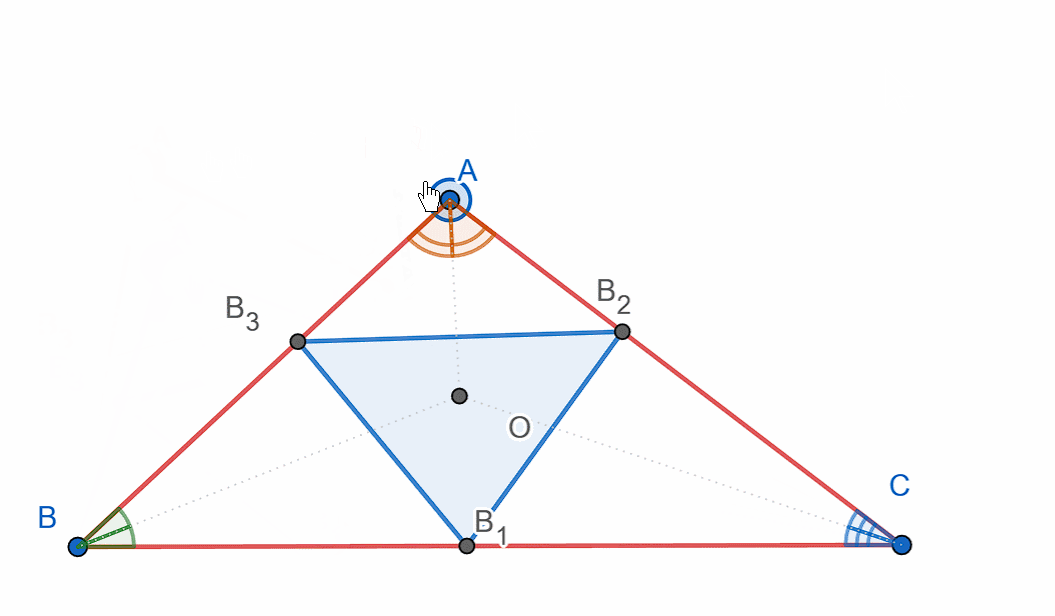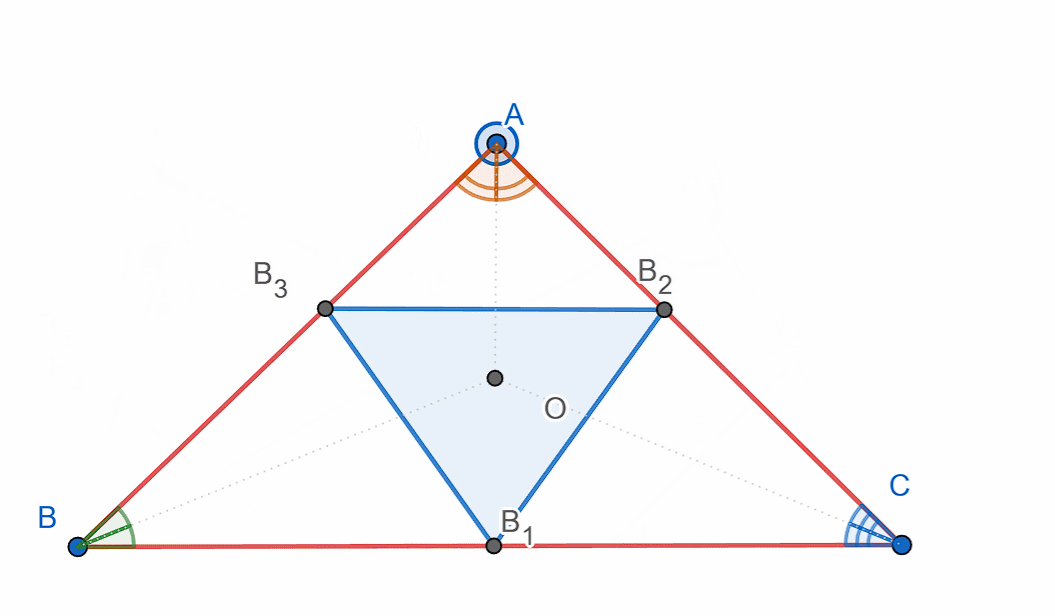
‼️You must construct and show the incircle triangle – the triangle formed by the feet of the angle bisectors.

Task 6

Display Four Triangles Together
Draw the four triangles: the main triangle ABC, and the triangles formed by the bases of the altitudes, angle bisectors, and medians.
There should be four (or three) triangles on the drawing. (It is normal for the triangle formed by the bases of the altitudes to disappear.)

‼️You must construct and show four triangles: the main triangle and the three triangles formed by the altitudes, medians, and angle bisectors.
Note: The orthic triangle may not always be visible.

All tasks 1,6 points, the sixth one 2.

Rules for Participation

Title of your work: SLC S23 Week2 || Geometry with GeoGebra: The Triangle and Its Elements

You can publish your work in any language, in any community, or simply in your own blog. Add the link to your work below as a comment.

To help me quickly find, review, and evaluate your work, leave the link in the comment under this text, and in your work, use the tag #gwgg-slc23w2

Each task response must include at least one image and one video (GIF) demonstrating the process of construction/solving.
You can use tools like GifCam as I did.
Note: The video/GIF will have the most significant impact on the evaluation.

Plagiarism and the use of AI are prohibited.

Participants must be verified and active users of the platform.

All images used must belong to the author or be free of copyright. (Don’t forget to credit the source.)

Participants must not use any bot services for voting or engage in vote buying.

Recommend your friends to participate.

Submission Period: From Monday (February 24/2025), to Sunday (March 2/ 2025).

Your work will be reviewed, commented on, and evaluated by me. Four best works will be selected.

Good luck 🍀 on your task!

_{Posted using SteemPro}

SLC S23 Week2 || Geometry with GeoGebra: The △riangle and Its Elements△