Hello to all my fellow Steemians! You may not know this about me, but I am a huge mathematics nerd. Seriously, I watch Youtube videos on advanced math concepts for a few hours each day for fun. Today, I would like to share with you what I think (and what many other mathematicians think) is the most beautiful and elegant concept in all of mathematics: Euler's Identity. This is my third achievement post under @cmp2020's program in the Steem Greet community.
The Identity
In its simplest terms, Euler's Identity (also known as Euler's Equation) is this equality statement:
(eiπ)+1=0
The Mathematical Beauty
For my non-mathematics enthusiasts out there, I am sure you are wondering, "Why do I care? What makes this so beautiful?" The amazing thing about Euler's Identity is that it combines five famous numbers in mathematics in a very unexpected way. e is known as Euler's number and is the natural base. i, an imaginary number, is the square root of -1. π is
"the the ratio of the circumference of a circle to its diameter."
1 is known as the multiplicative identity because you can multiply any number by 1 without changing the original number you are multiplying 1 with. Similarly, 0 is known as the additive identity because you can add 0 to any number and still get the original number.
My source for this section is the Wikipedia page titled Euler's identity
The Visual Beauty
For my more aesthetic and artistic people out there, here is an animation of Euler's Identity that was created by Wikipedia user Sbyrnes321 using Wolfram's Mathematica computer program:
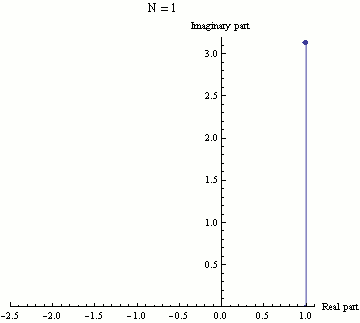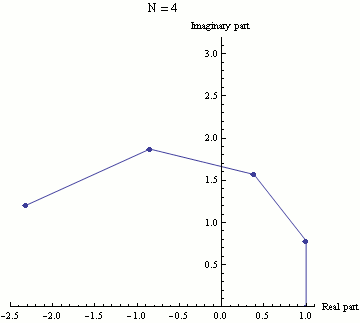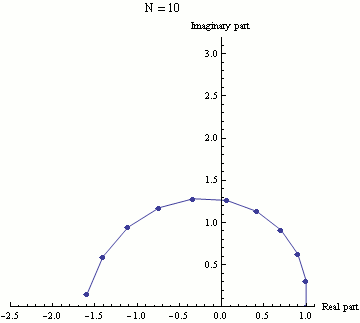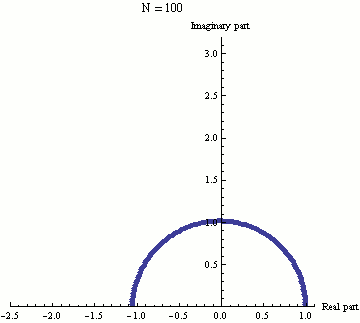.gif)
Conclusion
This is not meant to be an expansive, in-depth post or proof of Euler's Identity, but I just wanted to take a moment to highlight its mathematical significance and beauty. Thank you for reading this post. I hope I demonstrated my ability to use proper Steemit etiquette.
Nice post Jmor!
I can't exactly say I understood it (considering I am a math muggle), but it definitely fits the criteria for posting etiquette! You can find the information on the next achievement here.
Best regards!
@cmp2020
Steem Greeter
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you Chris! I was considering adding a section about the proof of the identity, but I didn't really want to get into Taylor Series and other advanced Calculus II and Complex Analysis concepts. Glad you liked it though.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You have been upvoted by Steem Greeters from STEEM POD Project and we are voting with the Steemit Community Curator @steemcurator03 account to support the newcomers coming into steemit.
Please follow @steemitblog for the latest update and news on steem and @steemingcurators for Steem Community contest and challenges.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit