SLC S23 Semana 1 || Geometría con GeoGebra: Puntos, Líneas y Ángulos

_F

Tarea Nº 1
¿Qué es la geometría? Cuándo y por qué apareció? Cómo estudiaste geometría en el colegio? Conocías algún programa informático de geometría?

¿Qué es la geometría?

La geometría es una palabra de origen griego ‘geo’ que significa ‘tierra’ y ‘metrein’ que significa ‘medir’.

En general, es una rama multifacética de las matemáticas sin embargo, el término se asocia comúnmente en su dimensión física con el estudio de las propiedades de las figuras en el plano o el espacio como puntos, rectas, planos cartesianos, polígonos, polícoros, etc.

No obstante, la geometría está estrechamente relacionada con otros dominios matemáticos, las ciencias naturales y sociales, sin exceptuar nuestra vida cotidiana.

¿Cuándo y cómo apareció?

No podemos decir que apareció de repente, sino que ha formado parte de un proceso en la historia de la Humanidad desde sus tiempos más remotos.

Nace en las comunidades más primitivas por el deseo de nuestros antepasados de representar al mundo circundante, decorar y diseñar objetos ornamentales, construir viviendas, entre otras necesidades cotidianas. De allí surgen los primeros diseños geométricos, la simetría y regularidad de las formas.

Luego del dominio de los aspectos visuales surgen civilizaciones como la babilónica pionera en el estudio de la geometría con la invención de la rueda y el estudio de la circunferencia, a la postre sucede el descubrimiento del número π (pi), el desarrollo del sistema sexagesimal al conocerse que el año cuenta con 365 días y la fórmula para calcular el área del trapecio rectángulo, entre otros relevantes.

En la búsqueda de mejorar la organización de la vida social, surgen civilizaciones importantes como la china, india, egipcia, griega, maya y azteca, enfocadas en resolver problemas prácticos como el trazado de linderos en la tierra, la medición de longitudes, áreas y volúmenes.

Así pasamos de las prácticas de medición empíricas de los egipcios y babilonios al fundamento teórico y deductivo del conocimiento geométrico de los griegos hacia la constitución de una disciplina científica axiomática.

La perfección del tratado de Euclides en su libro “Elementos” en el 300 a.C. se convirtió en modelo de sistematización racional en diversos campos por más de 2000 años. Así mismo lo acompañaron en este sistema las contribuciones de Apolonio, Arquímedes y Tolomeo.

La geometría no solo ha alcanzado el estatus de disciplina científica sino que está intrínsecamente vinculada con nuestra percepción espacial, hallando sus fuentes diversas, más allá de la investigación matemática, en las artes, los oficios, las técnicas y las ciencias.

Tal riqueza cultural permite a la geometría ubicarse en un lugar privilegiado en la enseñanza escolar por su aporte en la formación del individuo en sus diferentes aspectos, gracias a su característica multifacética que difícilmente otra rama de las matemáticas puede abarcar.

¿Cómo estudiaste geometría en el colegio? ¿Conocías algún programa informático de geometría?

Si me remonto a mi época de estudiante de primaria, estaría recordando el período 1.972-1.978. En mi Venezuela, la geometría se aprendía con transportador para medir ángulos, el compás para trazar círculos y una regla graduada para tomar medidas en la escala como herramientas útiles indispensables.

Generalmente, era instruido en manualidades y artes plásticas, por supuesto en las clases de matemáticas la maestra tomaba su tiza atada a un hilo para dibujar en la pizarra una circunferencia. Evidentemente, no existía un sistema un programa informático para la época.

Cuando transité la siguiente etapa en secundaria, entre 1.978 y 1.983, se continuaba utilizando el transportador, el compás, el escalímetro, una escuadra graduada equilátera o de 45º y una escuadra de triángulo rectángulo o de 90º/60º/30º. Se cursaba dibujo técnico para aplicar la geometría.

Para entonces los sistemas informáticos aún no llegaban a las instituciones educativas por tanto no se contaba menos aún con un programa informático de geometría.

_{Mi reliquia CASIO FX-880P aún funciona}
En mi etapa universitaria, entre 1.984 y 1.989, casi en la mitad de mi carrera se contaba con acceso limitado a una computadora IBM restringido a los estudiantes de sistemas.

Para la época llegué a tener una calculadora científica programable en lenguaje Basic, marca CASIO FX-880P que aún conservo, muy buena para resolver problemas de matemáticas, estructuras, estadísticas, etc. Cuenta con una librería de programas, pero no cuenta con una pantalla gráfica.

Sin duda un grato recuerdo...!

Tarea Nº 2
Explique las diferentes geometrías primitivas (punto, línea, ángulo, segmento, semirrecta) e ilústrelas en GeoGebra.

Punto

Uno de los conceptos fundamentales de la geometría euclidiana es el punto. Euclides la define como “aquello que no tiene parte”, es decir que es una figura geométrica que no tiene dimensión, longitud, área, volumen o ángulo dimensional. En las áreas de geometría analítica, diferencial y topología se dice que los objetos se construyen a partir de puntos.


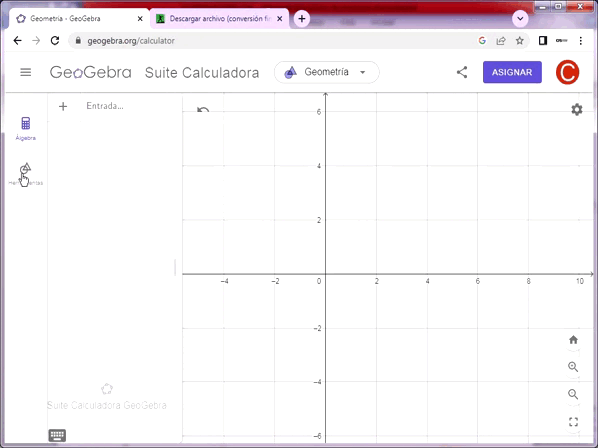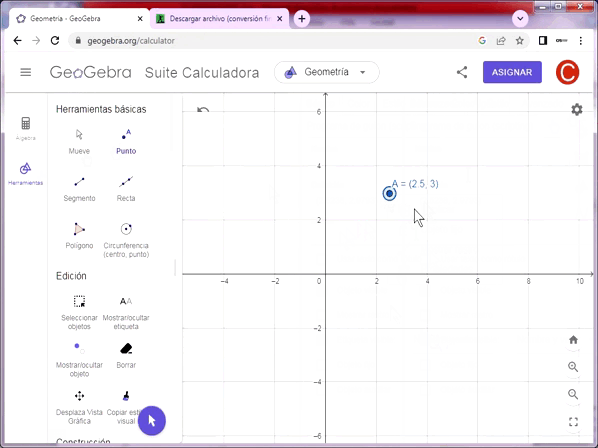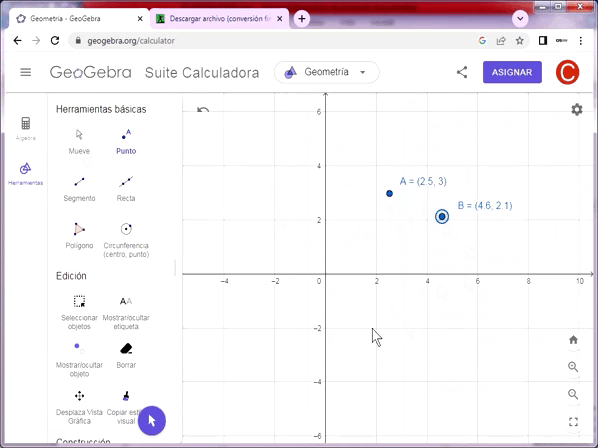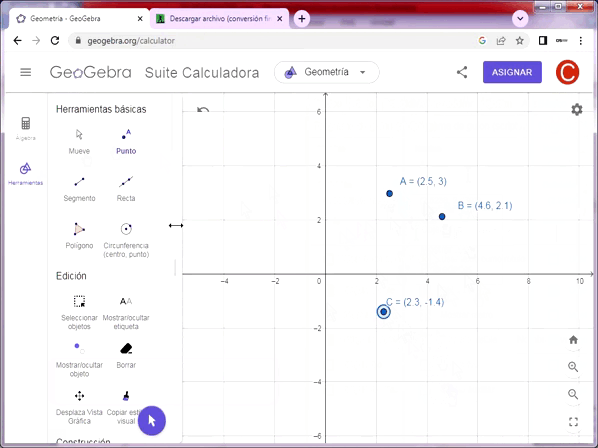
El punto no es un objeto físico y describe una posición en un plano de coordenadas preestablecido. Se denota con una letra mayúscula latina.


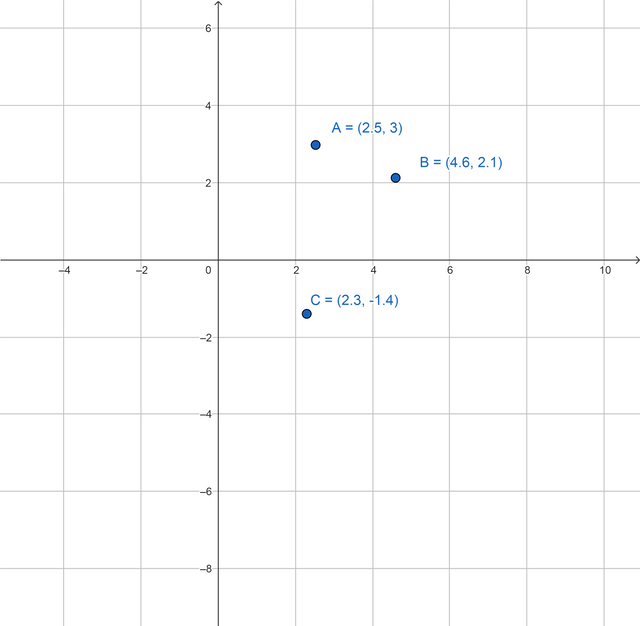
Línea

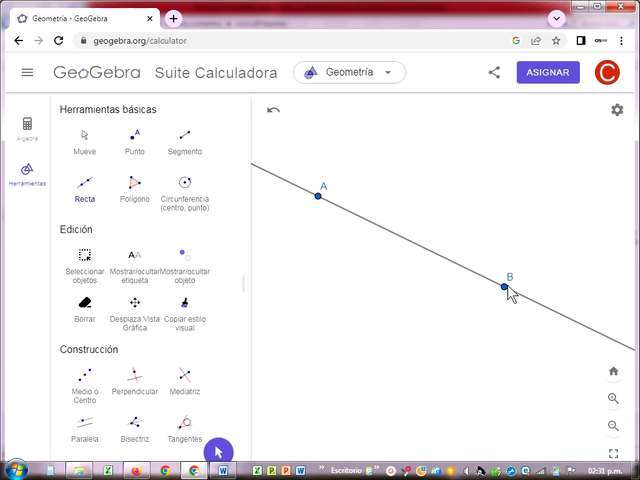
La línea es un conjunto de puntos continuos pertenecientes a un mismo plano que se extienden indefinidamente en ambas direcciones de una misma trayectoria. Es decir, no tienen un principio y un fin. La línea es unidimensional porque solo tiene longitud, carece de área, grosor o volumen.


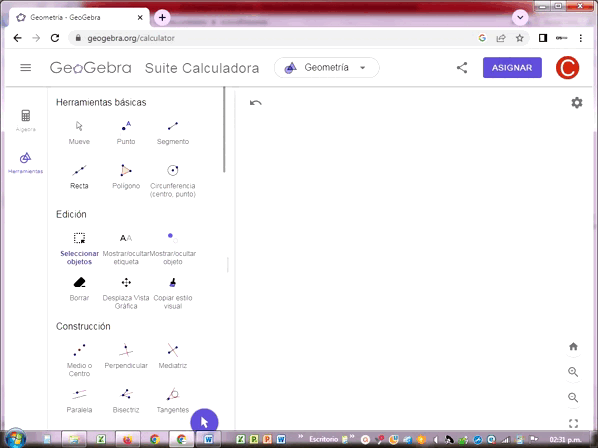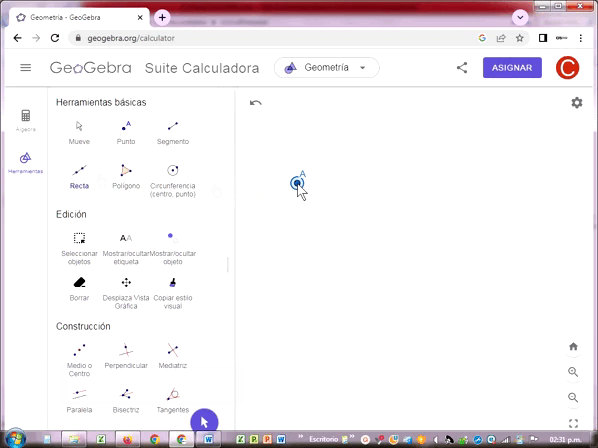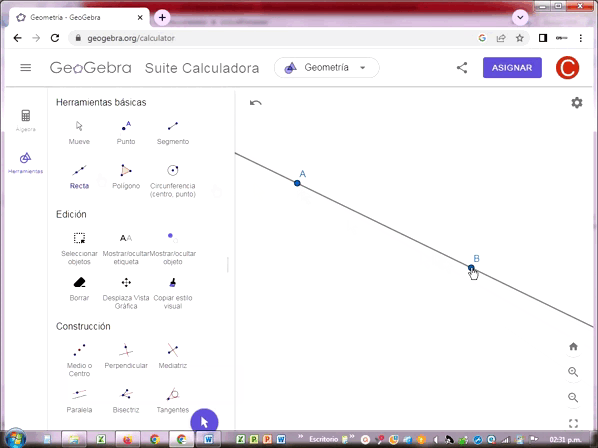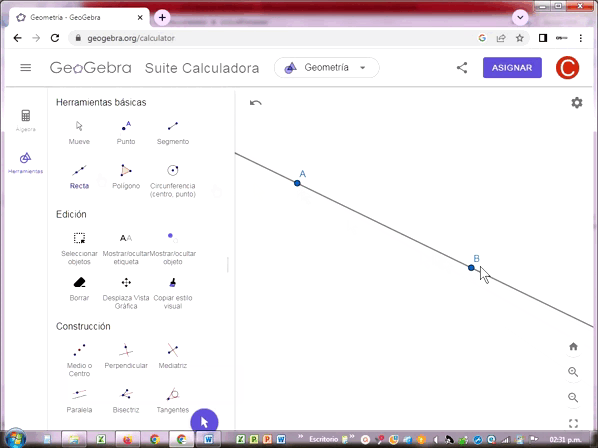
Básicamente por dos puntos solo puede pasar una línea recta. Se utilizan para componer otros objetos geométricos de mayor de complejidad.

Puede denotarse con dos letras mayúsculas o minúsculas latinas.


Ángulo

El ángulo es la porción del plano comprendida entre dos semirrectas o lados que comparten un punto de origen llamado vértice del ángulo. Es decir, las semirrectas parten de un mismo punto o vértice generando una apertura representada por un arco. El grado de apertura de este arco, no su extensión, representa el ángulo.


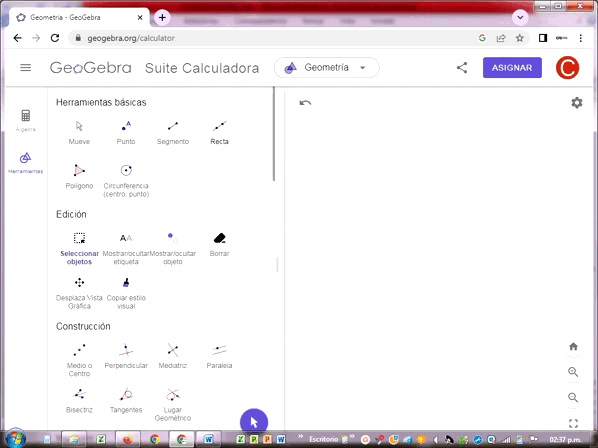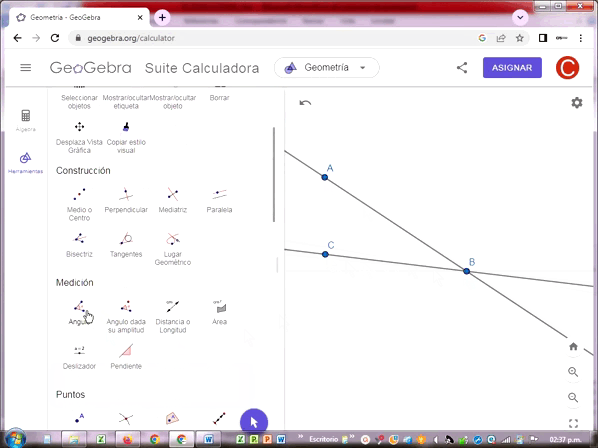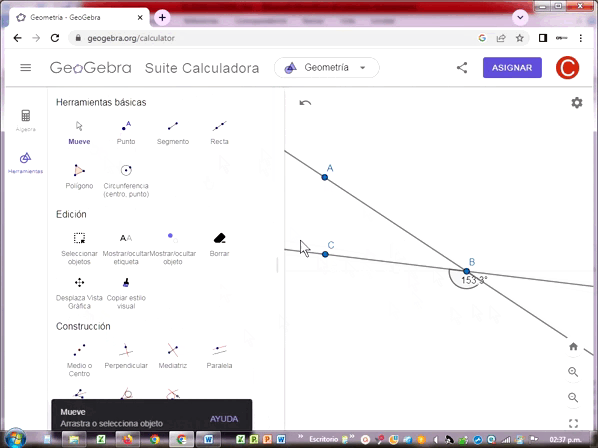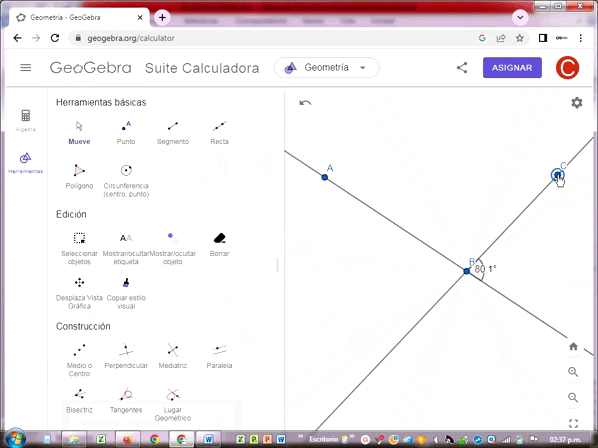
Los ángulos se miden generalmente en grados sexagesimales, es decir en base a un arco de círculo completo de 360º, cada grado equivale a 60 minutos, un minuto a 60 segundos, tal como se mide el tiempo en un reloj de agujas.

Existen otras formas de medir como radianes, donde el arco de un círculo completo mide 2 π (Pi) radianes.


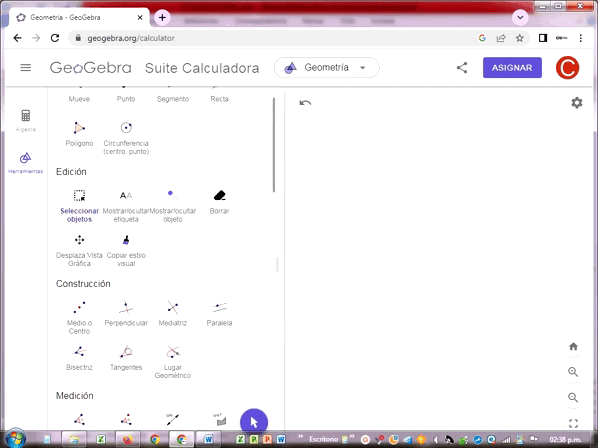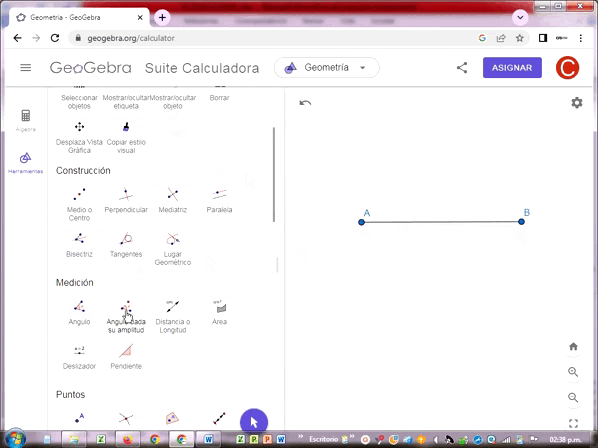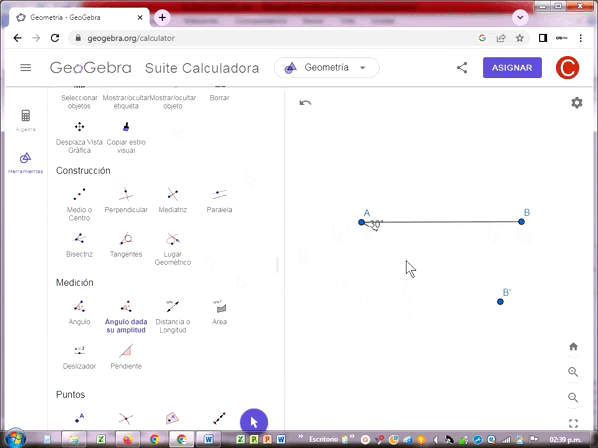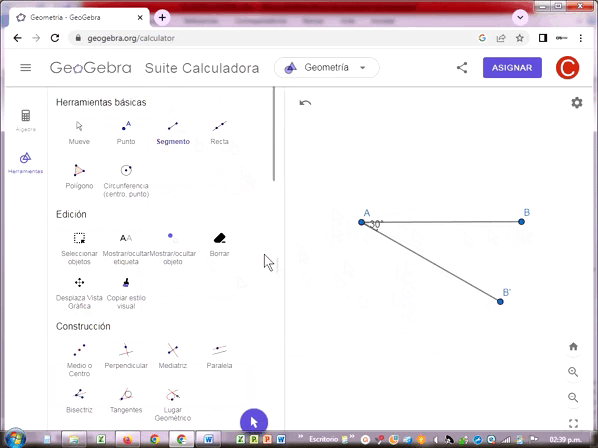
También se miden los ángulos entre dos rectas que tienen un vértice común. En este caso, los ángulos se pueden medir en los cuatro cuadrantes que circundan el vértice.


Suelen utilizarse letras griegas para representar los ángulos y diferenciarlas de otros, aunque resulta conveniente colocar su valor visualmente en el plano.

Segmento

El segmento es una parte de una recta delimitada por dos puntos que representan sus extremos inicial y final. También suelen denotarse con dos letras mayúsculas latinas.



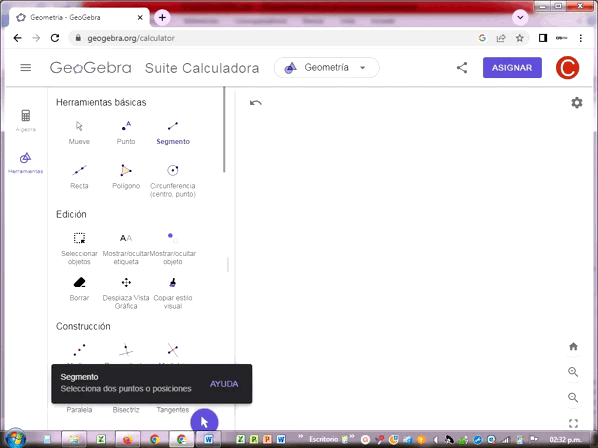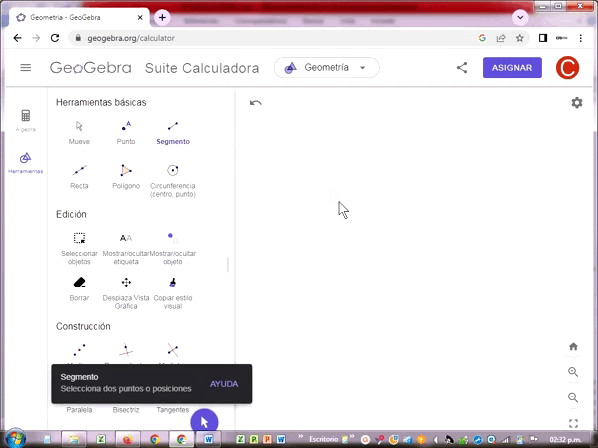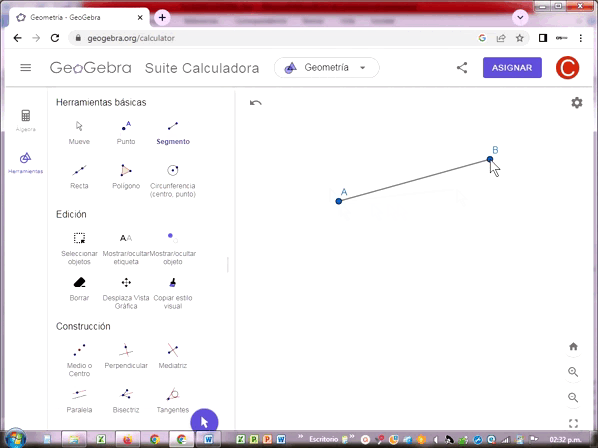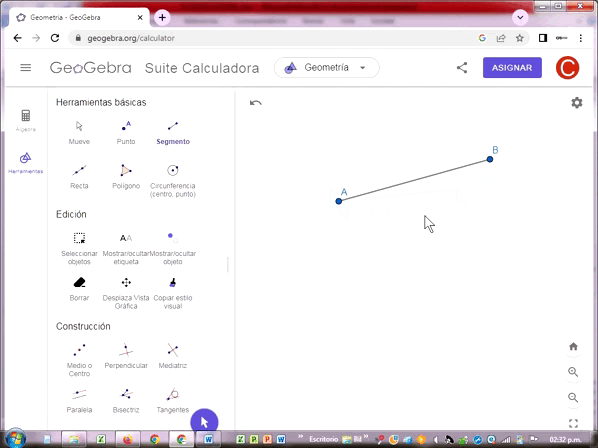
Semirrecta

Una semirrecta es una recta que tiene un punto de inicio pero no tiene un punto final. Cuando un punto divide una recta se forman dos semirrectas, cada una con un punto de inicio común. Se suele denotar con una letra latina mayúscula en el punto de inicio y otra en cualquier punto de la semirrecta.

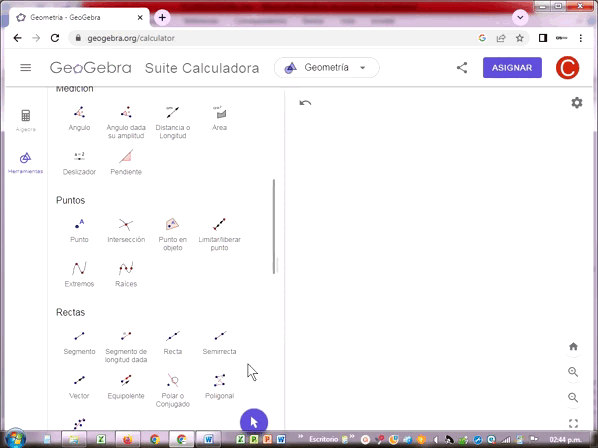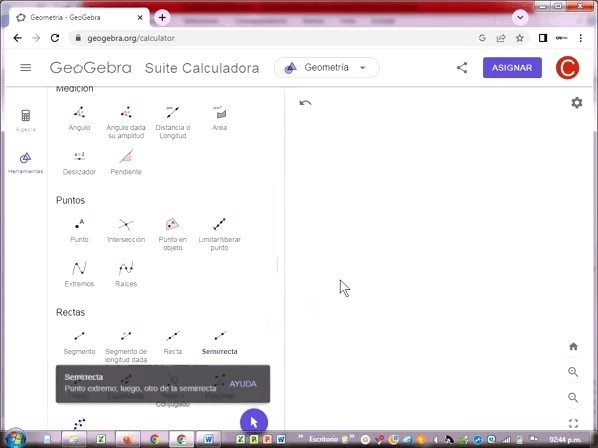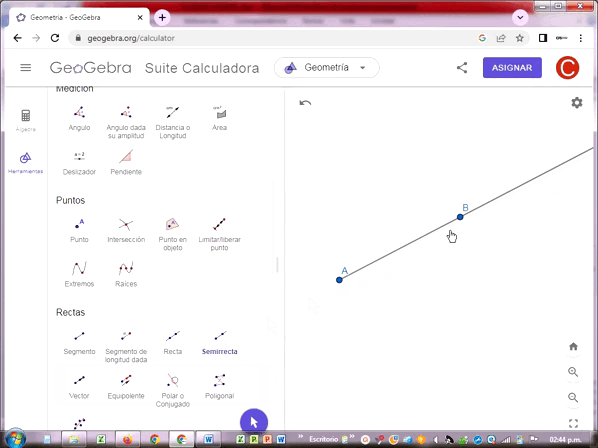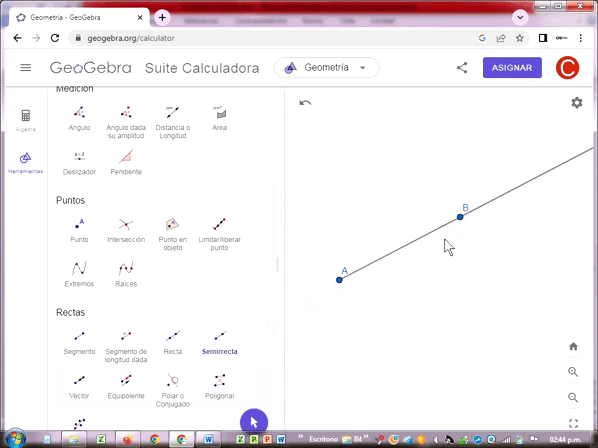
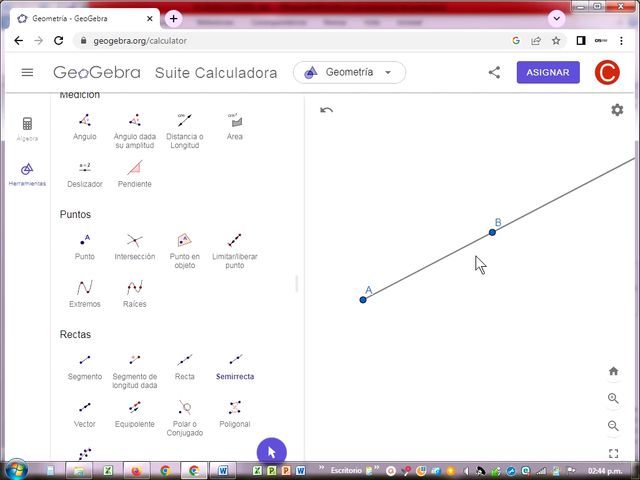
Tarea Nº 3

♦ Construye un ángulo arbitrario y prolonga uno de sus lados para crear una semirrecta suplementaria. Demuestra que la suma de los ángulos adyacentes es siempre 180 grados.

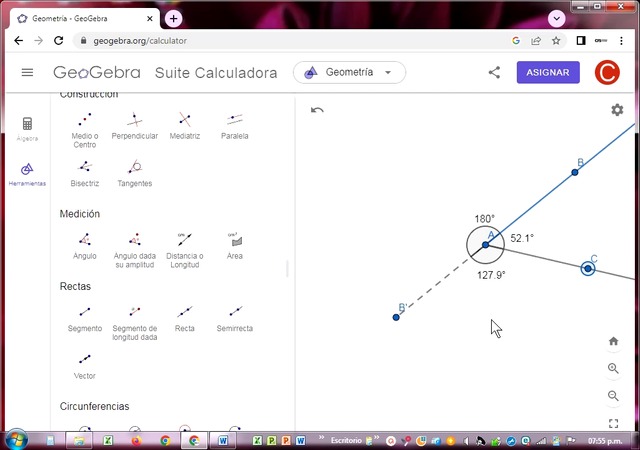
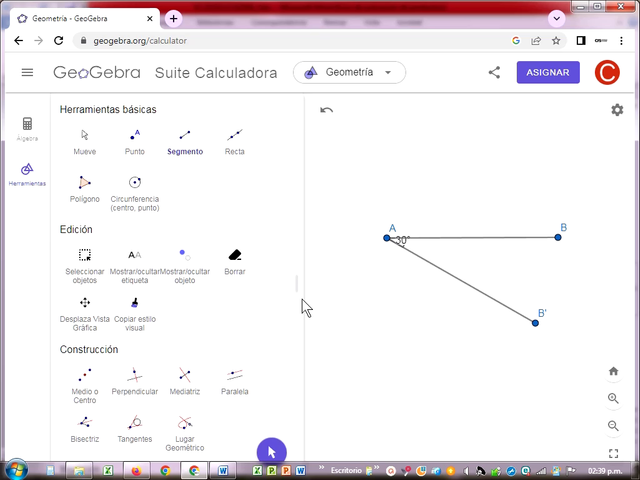
Cuando hice la extensión de la semirrecta AB, solo es posible a 180º como se demuestra en el gráfico en la línea discontinua de A a B’. Trace una semirrecta AC que inicia en A formando dos ángulos adyacentes con la semirrecta AB: 52.1º y 127.9º.

Por tanto se comprueba la suma de los ángulos adyacentes 52.1º+127.9º = 180.0º

♦ Construye un ángulo con dos rayos suplementarios y demuestra que los ángulos verticales resultantes son siempre iguales.

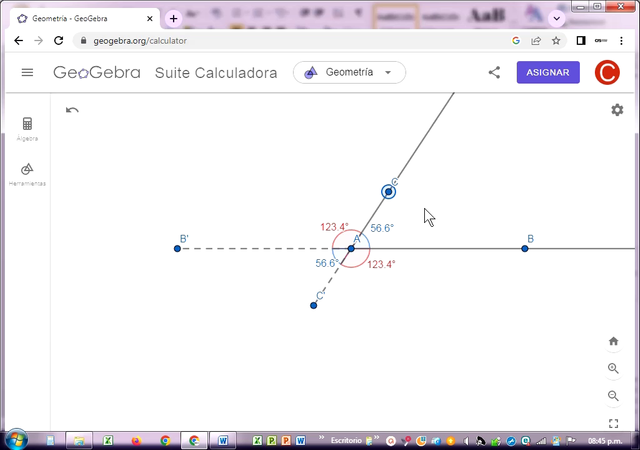
En este caso, construí dos semirrectas AB y AC, con sus respectivas extensiones denotadas con B’ y C’, en líneas discontinuas. Los ángulos verticales resultantes en color rojo son iguales a 123.4º y los ángulos adyacentes a éstos en color azul son iguales a 56.6º.

Se cumple que los ángulos verticales son siempre iguales.

Tarea Nº 4
♦ Construye rectas paralelas y rectas perpendiculares.

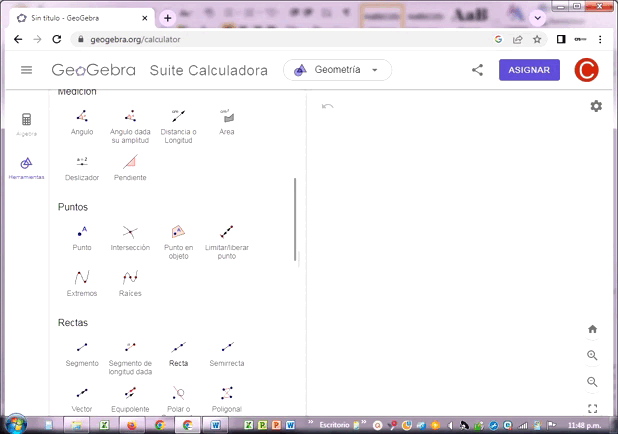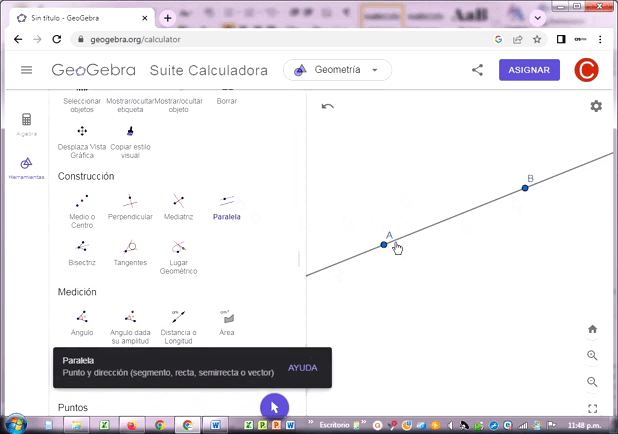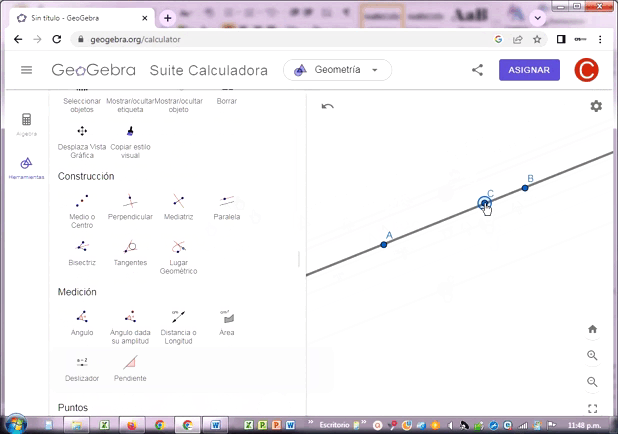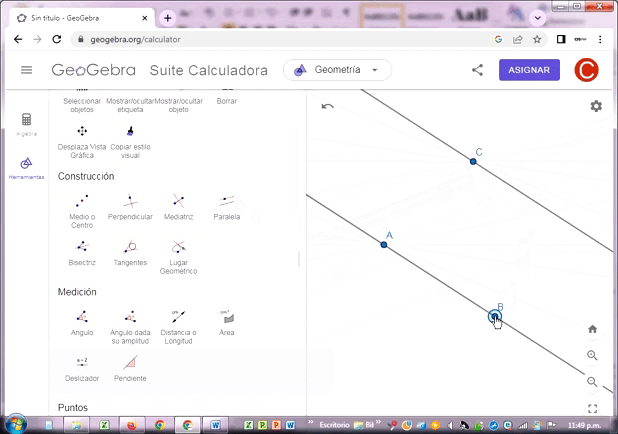
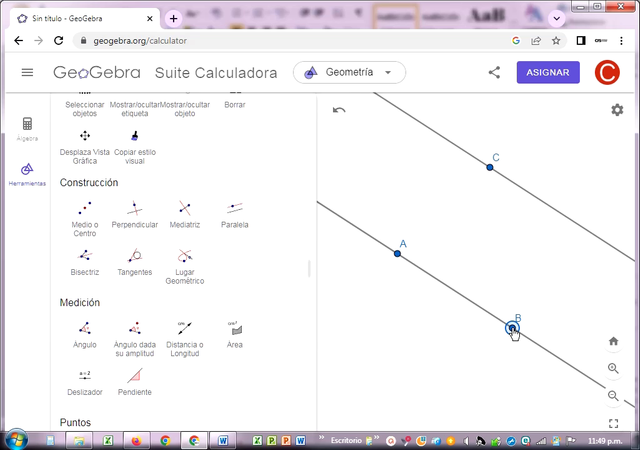
Las rectas paralelas AB y CD no se intersectan entre sí, porque pertenecen a planos paralelos. La distancia perpendicular a ellas es siempre la misma en cualquier posición en que se roten.



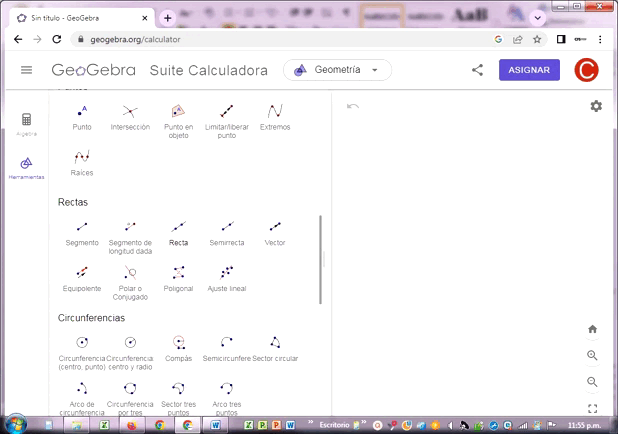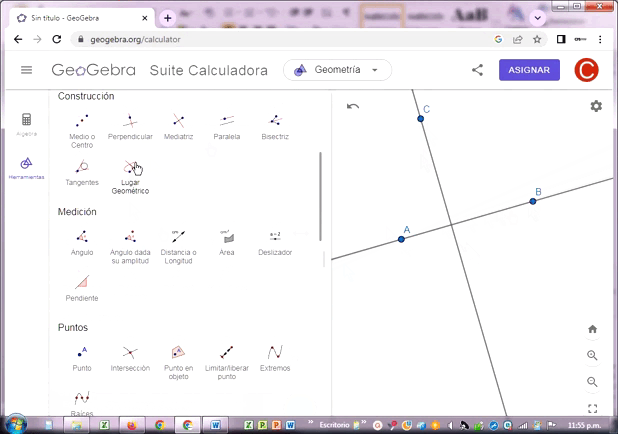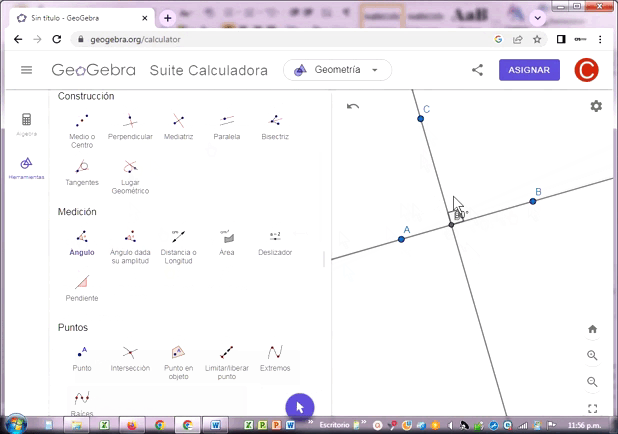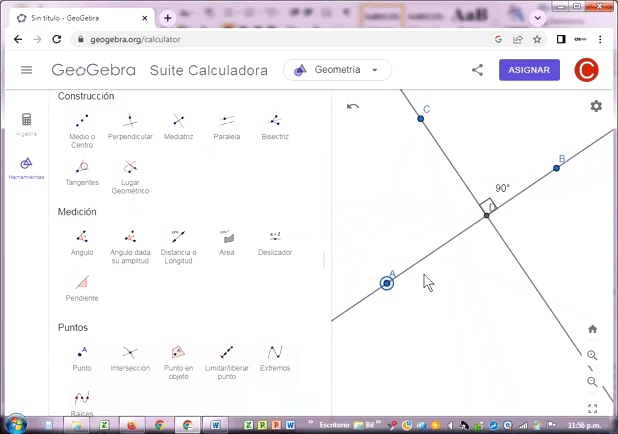
Las rectas AB y CD se intersectan en el punto D, de tal manera que la condición esencial es que se las rectas formen un ángulo recto (90º), tal como se muestra en el gráfico.

♦ Construye dos rectas intersectadas por una tercera recta (una transversal). Etiqueta los ángulos en la figura (usando letras, números o colores). Nombra los pares de ángulos que tienen nombres especiales.

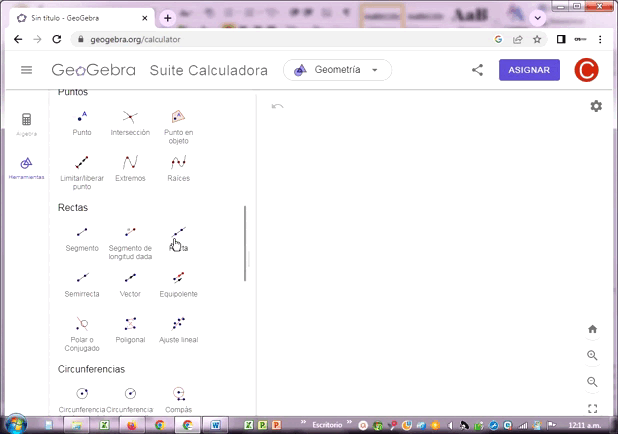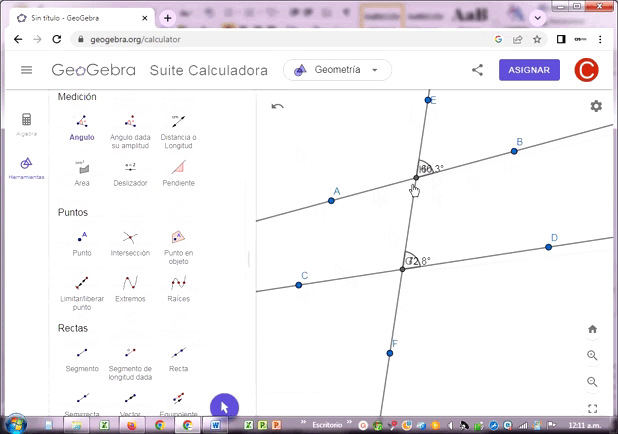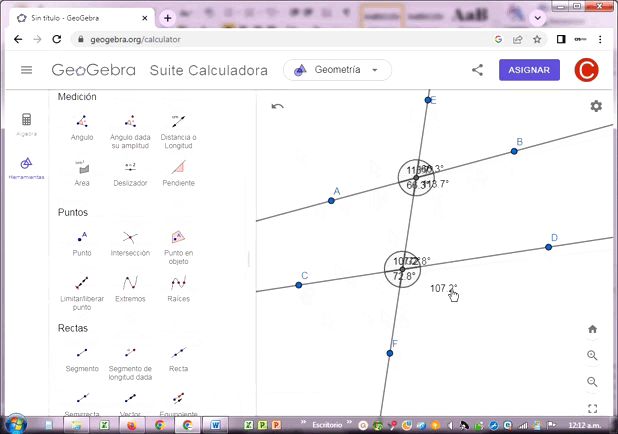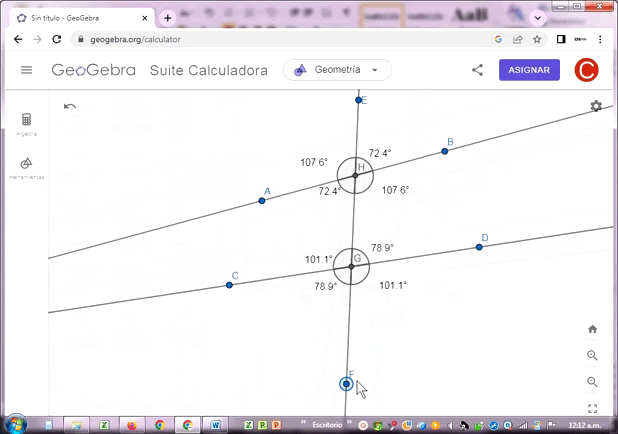
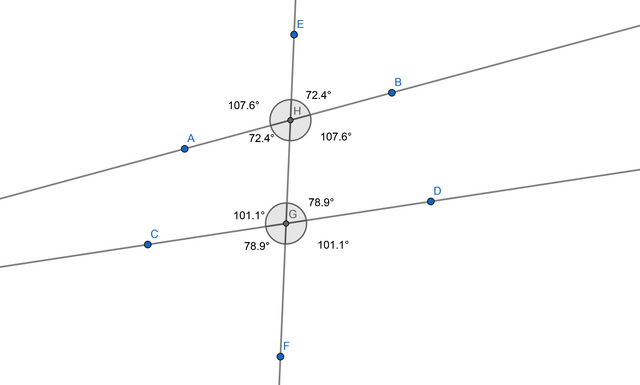
Construí tres rectas AB, CD y EF. La tercera recta intersecta a las dos primeras en los puntos H y G, determinados con la aplicación. El resultado final tienes los siguientes pares de ángulos ubicados en cada punto de intersección:

Ángulos verticales:

Intersección H (72.4º, 72.4º), (107.6º,107.6º)
Intersección G (78.9º,78.9º), (101.1º,101.1º)

Ángulos adyacentes:
Intersección H (107.6º, 72.4º), (72.4º,107.6º)
Intersección H (107.6º, 72.4º), (72.4º,107.6º)

Intersección G (101.1º,78.9º), (78.9º,101.1º)
Intersección G (101.1º,78.9º), (78.9º,101.1º)

Ángulos interiores del mismo lado:
(107.6º, 78.9º), (72.4º,101.1º)

Ángulos interiores de diferentes lado:
(72.4º, 78.9º), (107.6º,101.1º)

Ángulos correspondientes:
(107.6º, 101.1º), (72.4º, 78.9º)
(72.4º, 78.9º), (107.6º,101.1º)

Tarea Nº 5
Construye la intersección de dos segmentos. Asegúrate de que siempre se muestre el punto de intersección, aunque no se encuentre en los segmentos. Si el punto de intersección se encuentra fuera de los segmentos, represéntalo con líneas discontinuas.

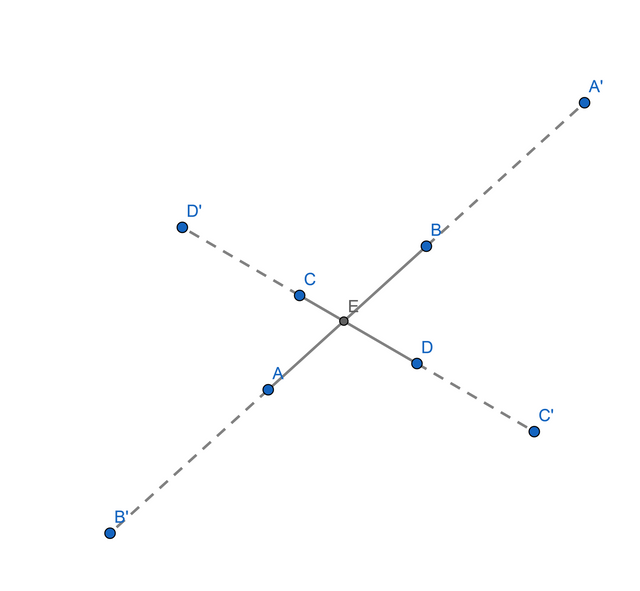
Construí dos segmentos AB y CD determinando el punto de intersección E. Para garantizar el punto de intersección fuera del segmento fue necesario construir extensiones en ambos extremos identificados con línea discontinuas en cada segmento. En estas extensiones también se marcan las intersecciones F,G,H,I, J, K , L y M, que se pueden observar en el GIF.

Efectivamente la aplicación Geogebra ofrece una facilidad para construir y realizar ajustes en línea, lo que nos regala un tiempo muy valioso para el análisis y el pensamiento creativo.

Notas:

📌 Imágenes propias con Online converter y Active Presenter para los capture de pantalla
📌 Invito a participar a mis amigos @paholags @marito74 @genomil @cruzamilcar63 @dove11 @goodybest
📌 Más información del concurso en el siguiente enlace.
📌 Mi twitter: steemit_casv

¡Gracias por su visita!