03-11-2024 - Education - Linear Algebra - determinant of square matrices

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
03-11-2024 - Education - Linear Algebra - determinant of square matrices[EN]-[IT]
With this post I would like to provide some brief notions regarding the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry
(code notes: MOD-85)

Determinant of square matrices
First of all, let's start by saying that the determinant of a matrix is ​​defined only for square matrices, that is, matrices with the same number of rows and columns.

The absolute value of the determinant of a square matrix represents the change in area or volume. The area would represent the two dimensions while the volume represents the three dimensions.

When the determinant is 0, the transformation flattens the space in a lower dimension and the matrix is ​​said to be singular and will not have an inverse.

If we take for example a space in two dimensions with a determinant of zero, the plane will be crushed into a line.

Properties of the determinant
-A matrix with a determinant other than zero is invertible. It means that there is another matrix that, multiplied by it, gives the identity matrix (or the starting one)
-Changes in sign of the determinant indicate inversions of orientation
-The determinant of a matrix is ​​equal to the product of the determinants of its diagonal matrices, if it is possible to decompose the matrix (for example by LU decomposition).

Calculation of the determinant
For a 2x2 matrix we will have the following.

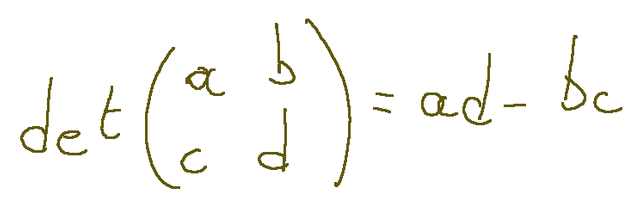
Example
Let's calculate the determinant of the following matrix

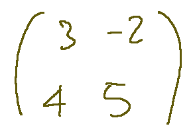
Remember that the determinant in this case is equal to the element a11 x a22 - a12 x a21

I report graphically below what described

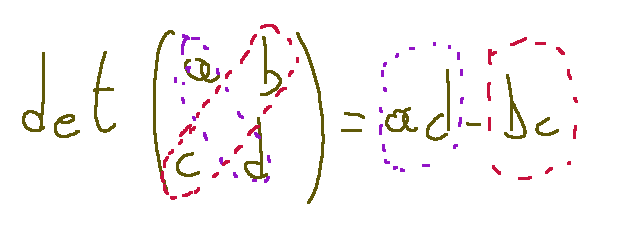
So in this case we will have that the determinant is (3x5)-(-2x4) = 23

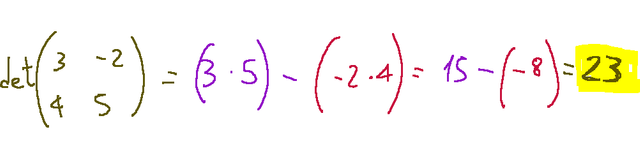
Conclusions
In analytic geometry and linear algebra, the determinant of a square matrix is ​​a number associated with the matrix that provides important information about various geometric and algebraic properties.

Question
Have you ever studied the determinant of a matrix in school?

---

---

[ITALIAN]
03-11-2024 - Education - Algebra lineare - determinante matrici quadrate[EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica
(code notes: MOD-85)

Determinante matrici quadrate
Per prima cosa iniziamo subito con il dire che il determinante di una matrice è definito solo per le matrici quadrate, ovvero matrici con lo stesso numero di righe e colonne.

Il valore assoluto del determinante di una matrice quadrata rappresenta la variazione di area o di volume. L'area rappresenterebbe le due dimensioni mentre il volume le tre dimensioni.

Quando il determinante è 0, la trasformazione appiattisce lo spazio in una dimensione inferiore e la matrice viene detta singolare e non avrà inversa.
Se prendiamo per esempio un spazio in due dimensioni con determinante zero il piano verrà schiacciato in una linea.

Proprietà del determinante
-Una matrice con determinante diverso da zero è invertibile. Significa che esiste un'altra matrice che , moltiplicata per essa, dà la matrice identità (o quella di partenza)
-Cambiamenti di segno del determinante indicano inversioni di orientamento
-Il determinante di una matrice è uguale al prodotto dei determinanti delle sue matrici diagonali, se è possibile decomporre la matrice (ad esempio tramite decomposizione LU).

Calcolo del determinante
Per una matrice 2x2 avremo quanto segue.

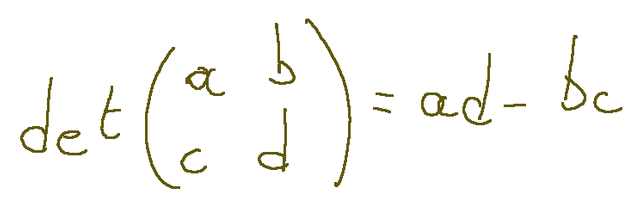
Esempio
Calcoliamo il determinante della seguente matrice

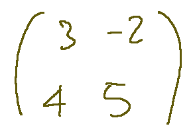
Ricordiamo che il determinante in questo caso è uguale all’elemento a11 x a22 - a12 x a21

Riporto graficamente qui sotto quanto descritto

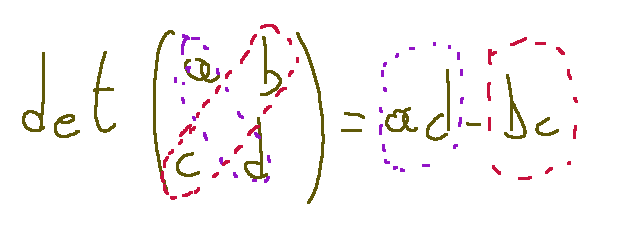
Quindi in questo caso avremo che il determinante è (3x5)-(-2x4) = 23

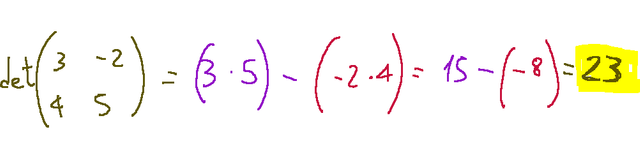
Conclusioni
In geometria analitica e in algebra lineare, il determinante di una matrice quadrata è un numero associato alla matrice che fornisce informazioni importanti su varie proprietà geometriche e algebriche.

Domanda
Avete mai studiato a scuola il determinante di una matrice?

THE END