03-11-2024 - Education - Linear Algebra - Invertible Matrices [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
03-11-2024 - Education - Linear Algebra - Invertible Matrices [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry
(code notes: MOD-86)

Invertible Matrices
Invertible matrices are matrices that have an inverse.
We can define them like this.
An inverse matrix is ​​a matrix A for which there exists another matrix B in such a way that what is described below happens.

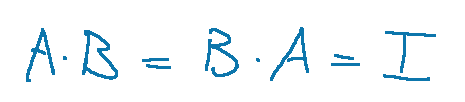
Invertibility Conditions
To be invertible a matrix must have two conditions.
1-Non-zero determinant.
A square matrix is ​​invertible if its determinant is different from zero. If the determinant is zero the matrix is ​​singular and has no inverse.
2-Maximum rank.
An n x n matrix must have rank equal to n. We can also say that the rank of an invertible matrix must be maximum, that is, equal to the size of the matrix itself.

The matrix In is invertible for every n, and its inverse is In itself, in fact we have In * In = In

Calculation
To calculate the inverse of a matrix like the following

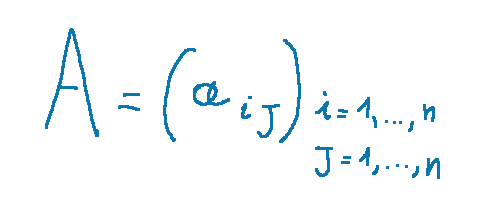
we have only one possibility which is to solve the following system.

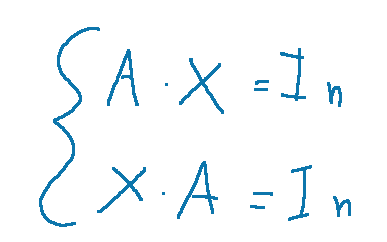
Example
Let's try to find the inverse matrix of the following matrix.

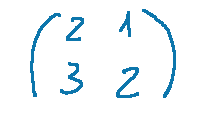
At this point we write the system that we have to consider

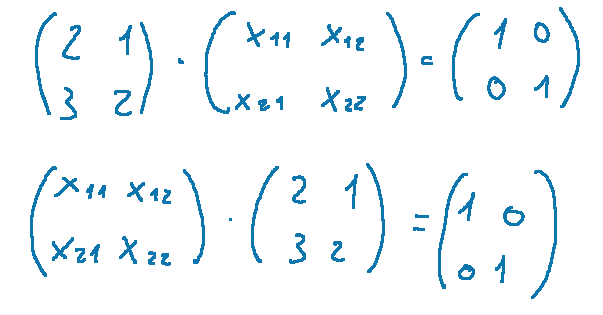
In this system the unknown is a matrix. Now let's do the two products for the columns and we will get the following.

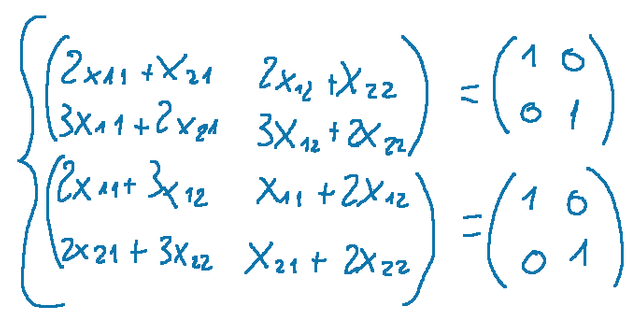We will obtain a system with 8 equations  Below is the complete system with the 8 equations 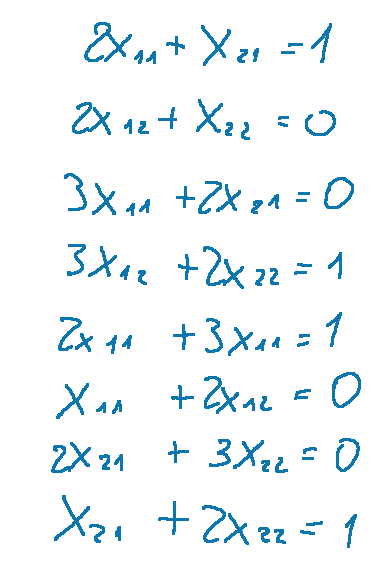The solution is the following quatern 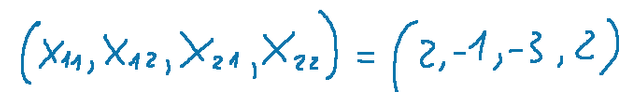then we will have that the inverse of the matrix...  is the following matrix...

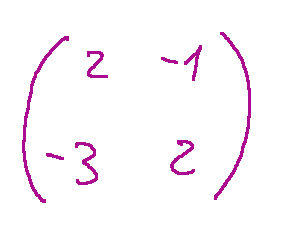
Conclusions
The inverse of a matrix is ​​useful in many mathematical and engineering applications, especially for solving linear systems.

Question
Do you think matrix operations are easy to understand or are they difficult?

---

---

[ITALIAN]
03-11-2024 - Education - Algebra lineare - Matrici invertibili [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica
(code notes: MOD-86)

Matrici invertibili
Le matrici invertibili sono matrici che possiedono un'inversa.
Possiamo definirle così.
Una matrice inversa è una matrice A per la quale esiste un'altra matrice B in maniera che avvenga ciò che è descritto qui di seguito.

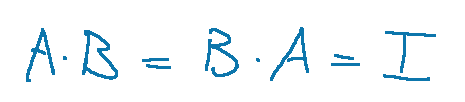
Condizioni di invertibilità
Per essere invertibile una matrice deve avere due condizioni.
1-Determinante non nullo.
Una matrice quadrata è invertibile se il suo determinante è diverso da zero. Se il determinante è zero la matrice è singolare e non ha inversa.
2-Rango massimo.
Una matrice n x n deve avere rango pari a n. Possiamo dire anche che il rango di una matrice invertibile deve essere massimo, cioè uguale alla dimensione della matrice stessa.

La matrice In è invertibile per ogni n, e la sua inversa è In stessa, infatti abbiamo In * In = In

Calcolo
Per calcolare l'inversa di una matrice come la seguente

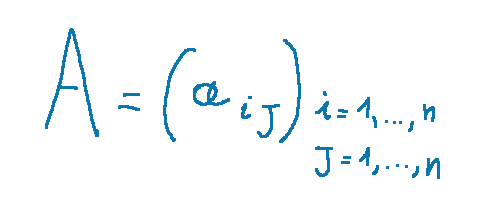
abbiamo una sola possibilità che è risolvere il seguente sistema.

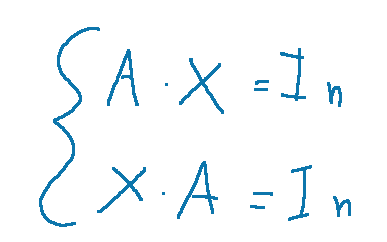
Esempio
Proviamo a trovare la matrice inversa della seguente matrice.

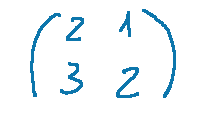
A questo punto scriviamo il sistema che dobbiamo considerare

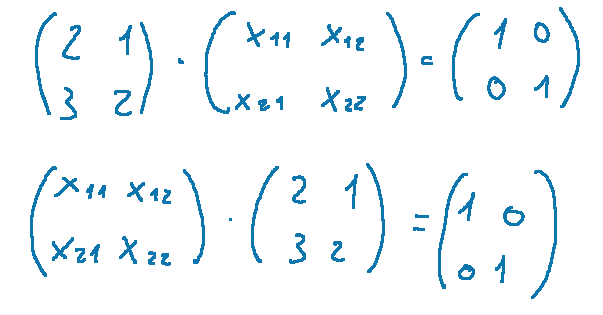
In questo sistema l'incognita è una matrice. Ora andiamo a fare i due prodotti per le colonne ed otterremo quanto segue.

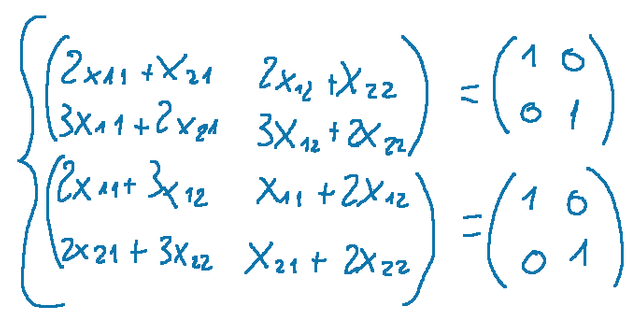
Otterremo un sistema con 8 equazioni

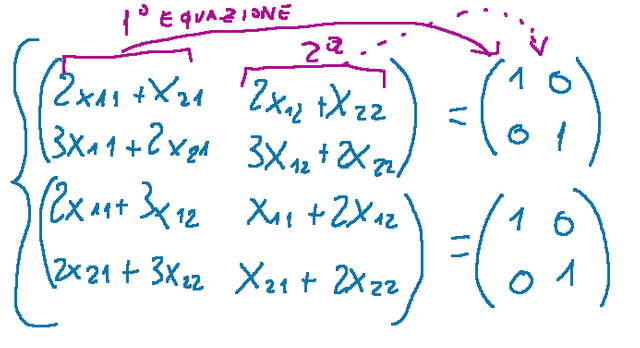
Qui di seguito il sistema completo con le 8 equazioni

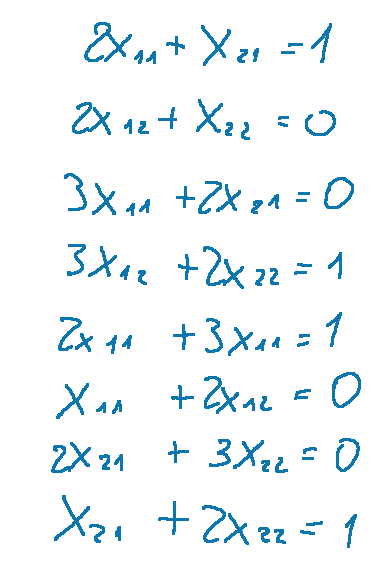
La soluzione è la quaterna seguente

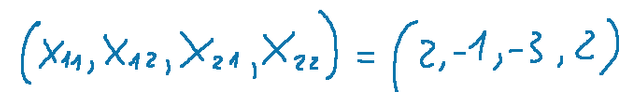
quindi avremo che l'inversa della matrice...

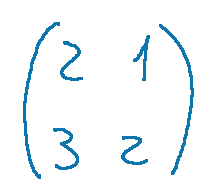
è la seguente matrice...

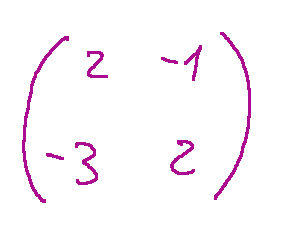
Conclusioni
L'inversa di una matrice è utile in molte applicazioni matematiche e ingegneristiche, in particolare per risolvere sistemi lineari.

Domanda
Secondo voi le operazioni tra matrici sono facilmente comprensibili o sono difficili?

THE END