04-11-2024 - Education - Linear algebra - finding the determinant [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
04-11-2024 - Education - Linear algebra - finding the determinant [EN]-[IT]
With this post I would like to provide some brief notions regarding the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-85)

finding the determinant
In this article today I try to show even more clearly than in the past how to calculate the determinant of a matrix.

Brief notions
The determinant of a matrix is ​​a number that we can find in each square matrix, that is, in an n x n matrix, or even better, in a matrix that has the same number of rows and columns.
The determinant of a matrix expresses some algebraic and geometric properties of the matrix itself.
Usually the determinant of the matrix A is indicated as follows: det(A)

Take for example a square matrix like the following

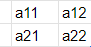
Its determinant is calculated as follows
det (a) = a11 x a22 - a12 x a21
That is, the product of one diagonal minus the product of the other diagonal.
Here is a drawing to better understand

Example with numerical matrix
At this point let's make an example with a matrix composed of numbers

Let's take the following matrix as an example:

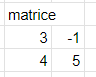
Let's remember how to calculate the determinant by taking as an example the first matrix that I described in this article

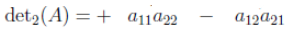
To find the number associated with the determinant we must therefore perform the multiplication of the members that make up the first diagonal and subtract them from the members of the second diagonal
Here is a screenshot for better understanding.

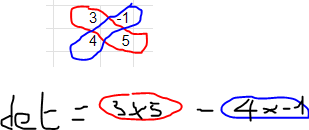
We will get the following result

Below is a screenshot with added colors to better understand what we have done

So the result of this example is 19

Conclusions
The determinant of a matrix is ​​important because it immediately lets you understand whether the matrix is ​​invertible or not. The matrix is ​​invertible if the determinant is different from 0

Question
In my opinion, finding the determinant of 2 x 2 square matrices is quite simple, while things get complicated as soon as we move to 3 x 3 matrices. Is this the case for you too?

---

---

[ITALIAN]
04-11-2024 - Education - Algebra lineare - trovare il determinante [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-85)

trovare il determinante
In questo articolo di oggi provo a mostrare ancora più chiaramente delle volte scorse come si calcola il determinante di una matrice.

Brevi nozioni
Il determinante di una matrice è un numero che possiamo trovare in ciascuna matrice quadrata, cioè in una matrice n x n, o ancora meglio, in una matrice che ha lo stesso numero di righe e di colonne.
Il determinante di una matrice esprime alcune proprietà algebriche e geometriche della matrice stessa.
Solitamente il determinante della matrice A si indica come segue: det(A)

Prendiamo per esempio una matrice quadrata come la seguente

Il suo determinante si calcola così
det (a) = a11 x a22 - a12 x a21
Cioè il prodotto di una diagonale meno il prodotto dell'altra diagonale.
Qui di seguito uno disegno per capire meglio

Esempio con matrice numerica
A questo punto facciamo un esempio con una matrice composta da numeri

Prendiamo come esempio la seguente matrice:

Ricordiamo come si calcola il determinante prendendo come esempio la prima matrice che ho descritto in questo articolo

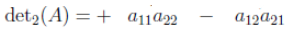
Per trovare il numero associato al determinante dobbiamo quindi eseguire la moltiplicazione dei membri che compongono la prima diagonale e sottrarli ai membri della seconda diagonale
Qui si seguito uno screenshot per maggiore comprensione.

Otterremo il seguente risultato

Qui di seguito uno screenshot con l'aggiunta di colori per comprendere meglio ciò che abbiamo eseguito

Quindi il risultato di questo esempio è 19

Conclusioni
Il determinante di una matrice è importante in quanto fa comprendere immediatamente se la matrice è invertibile oppure no. La matrice è invertibile se il determinante è diverso da 0

Domanda
Secondo me trovare il determinante di matrici quadrate 2 x 2 è abbastanza semplice, mentre le cose si complicano appena ci spostiamo su matrici 3 x 3. Anche per voi è così?

THE END