09-11-2024 - Education - Linear algebra - non-invertible matrices [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
09-11-2024 - Education - Linear algebra - non-invertible matrices [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-82)

non-invertible matrices
A matrix is ​​invertible if det n(A) is different from 0

Example 01
So let's now try to verify whether the following matrix is ​​invertible or not.

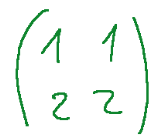
First we must verify that its determinant is different from zero.
Recall that a square matrix is ​​invertible if and only if its determinant is different from zero.
For a 2 x 2 matrix, the determinant is given by the following operation.

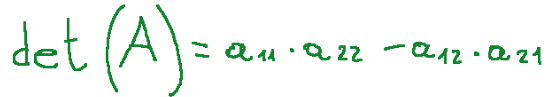
In this case we will have this situation
Where:
a11​=1
a12​=1
a21​=2
a22​=2

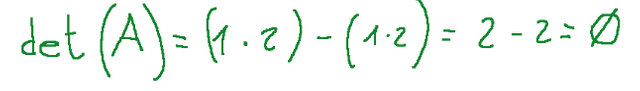
Result
Since the determinant of A is zero, the matrix is ​​not invertible.

Example 02
Let's now try to see if the following 3x3 matrix is ​​invertible.

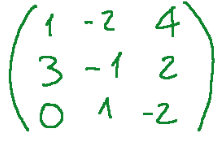
What we will do is calculate the determinant.
For a 3×3 matrix, the determinant can be calculated using Sarrus' rule or Laplace expansion along a row or column. Let's use the Laplace expansion along the first line:

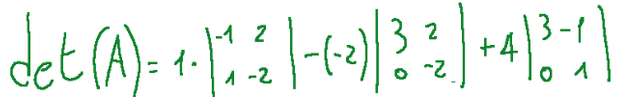
Let's calculate each determinant of the 2x2 matrices
Determinant of the first minor

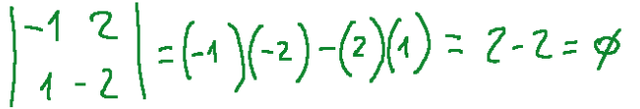
Determinant of the second minor:

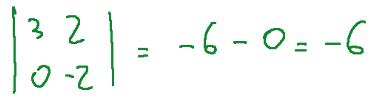
Determinant of the minor third:

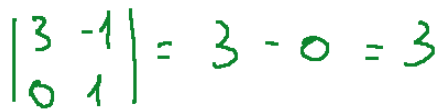
So let's complete the calculation of the determinant

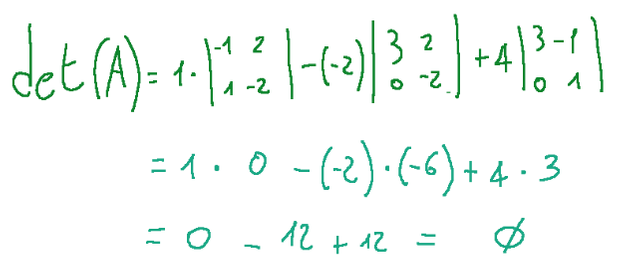
Result
Since the determinant of A is zero, the matrix is ​​not invertible.

Conclusions
When we want to understand if a matrix is ​​invertible, the first thing to do is to calculate the determinant. If the determinant of a matrix is ​​equal to 0, the matrix is ​​not invertible, if instead it is different from zero, the matrix is ​​invertible.

Question
Have you ever tried at school to understand if a matrix is ​​invertible or not?

---

---

[ITALIAN]
09-11-2024 - Education - Algebra lineare - matrici non invertibili [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-82)

matrici non invertibili
Una matrice è invertibile se det n(A) è diverso da 0

Esempio 01
Quindi proviamo ora a verificare se la seguente matrice è invertibile oppure no.

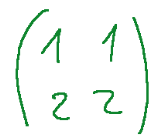
Per prima cosa dobbiamo verificare che il suo determinante sia diverso da zero.
Ricordiamo che una matrice quadrata è invertibile se e solo se il suo determinante è diverso da zero.
Per una matrice 2 x 2, il determinante è dato dalla seguente operazione.

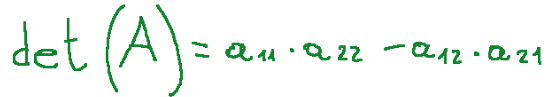
In questo caso avremo questa situazione
Dove:
a11​=1
a12​=1
a21​=2
a22​=2

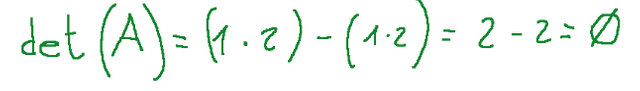
Risultato
Poiché il determinante di A è zero, la matrice non è invertibile.

Esempio 02
Proviamo ora a vedere se la seguente matrice 3x3 è invertibile.

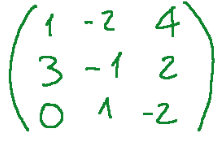
Ciò che faremo sarà calcolare il determinante.
Per una matrice 3×3, il determinante può essere calcolato usando la regola di Sarrus o lo sviluppo di Laplace lungo una riga o colonna. Usiamo lo sviluppo di Laplace lungo la prima riga:

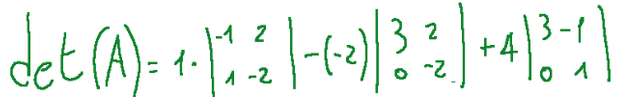
Andiamo a calcolare ogni determinante delle matrici 2x2
Determinante del primo minore

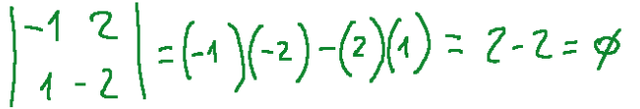
Determinante del secondo minore:

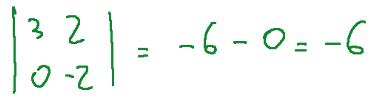
Determinante del terzo minore:

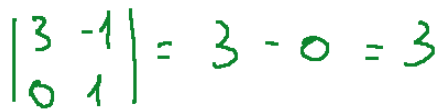
Quindi andiamo a completare il calcolo del determinante

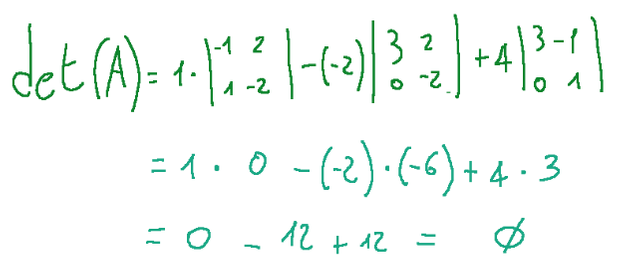
Risultato
Poiché il determinante di A è zero, la matrice non è invertibile.

Conclusioni
Quando vogliamo capire se una matrice è invertibile, la prima cosa da fare è calcolare il determinante. Se il determinante di una matrice è uguale a 0, la matrice non è invertibile, se invece è diverso da zero, la matrice è invertibile.

Domanda
Avete mai provato a scuola a comprendere se una matrice è invertibile oppure no?

THE END