10-13-2024 - Education - Geometry - linear combination of column vectors [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
10-13-2024 - Education - Geometry - linear combination of column vectors [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of energy machines.
(code notes: MOD-94)

linear combination of column vectors
Linear combinations of column vectors are a key concept in linear algebra. It involves combining multiple vectors using constants (scalars) to obtain a new vector.
Below is how to write 2 column vectors

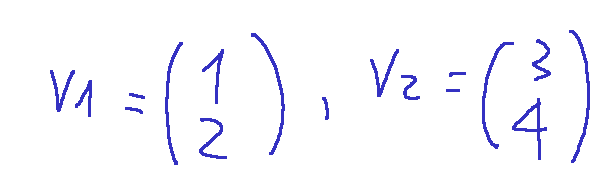
The linear combination of two column vectors is the sum of the two vectors multiplied by scalars.
Here is the graphical representation with scalars written as c1 and c2

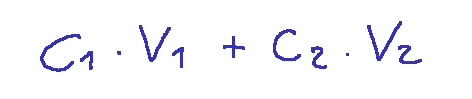
Here is the complete representation

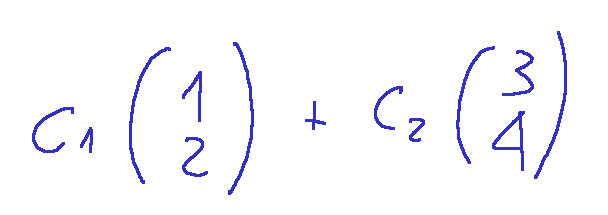
If we continue with the concept we will obtain a new vector that we can describe in this way.

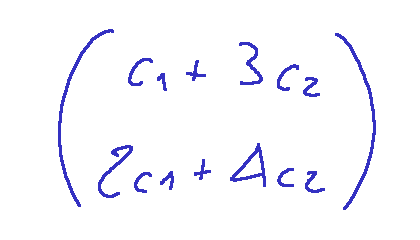
Example
Let's consider the linear combination of the following column vectors

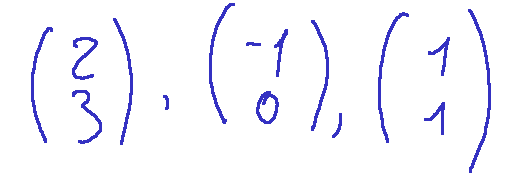
While for coefficients (scalars) we will use

We will have the following writing  Let's now execute the various products 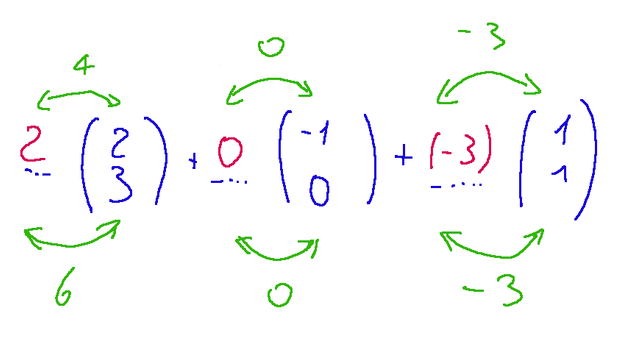And now let's execute the sums of the products

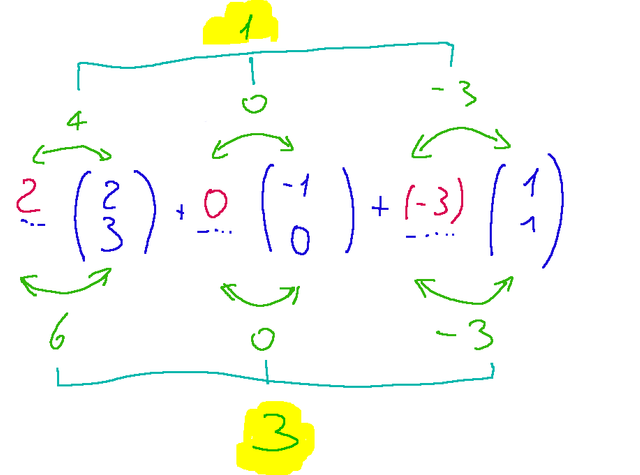
Result
We will have that the vector resulting from this linear combination of column vectors will be the following.

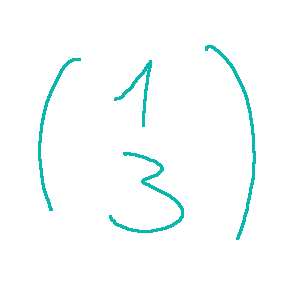
Conclusions
Linear combinations of column vectors are a key concept in linear algebra and analytical geometry. It involves combining multiple vectors using scalar numbers to obtain a new vector.

Question
Linear combinations of column vectors are a basic concept of analytic geometry or algebra, but not all schools teach them. Do you remember studying linear combinations of column vectors in school?

THE END

---

---

[ITALIAN]
13-10-2024 - Education - Geometria - combinazione lineare dei vettori colonna [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello delle macchine energetiche.
(code notes: MOD-94)

combinazione lineare dei vettori colonna
Le combinazioni lineari di vettori colonna sono un concetto chiave dell'algebra lineare. Si tratta di combinare più vettori usando delle costanti (scalari) per ottenere un nuovo vettore.
Qui di seguito è rappresentato come si scrivono 2 vettore colonna

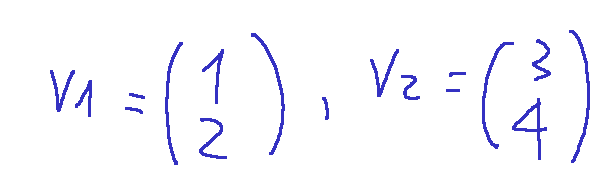
La combinazione lineare di due vettori colonna è la somma dei due vettori moltiplicata per degli scalari.
Qui di seguito la rappresentazione grafica con gli scalari scritti come c1 e c2

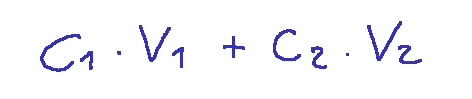
Qui di seguito la rappresentazione completa

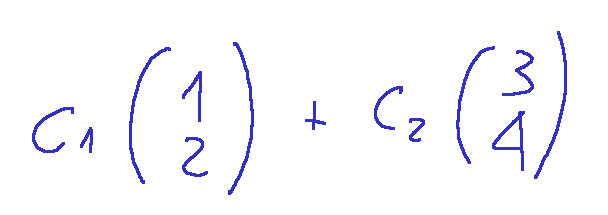
Se proseguiamo con il concetto otterremo un nuovo vettore che possiamo descrivere in questa maniera.

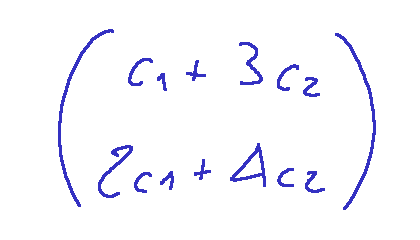
Esempio
Prendiamo in considerazione la combinazione lineare dei seguenti vettori colonna

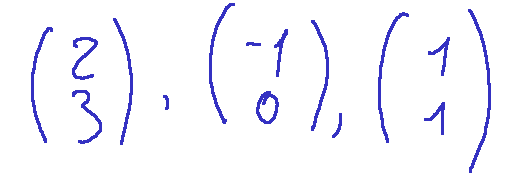
Mentre per coefficienti (scalari) useremo

Avremo la seguente scrittura

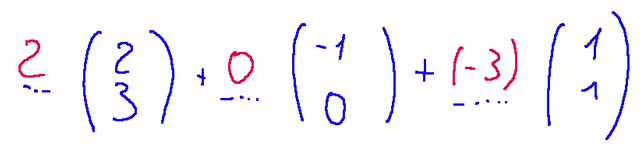
Eseguiamo ora i vari prodotti

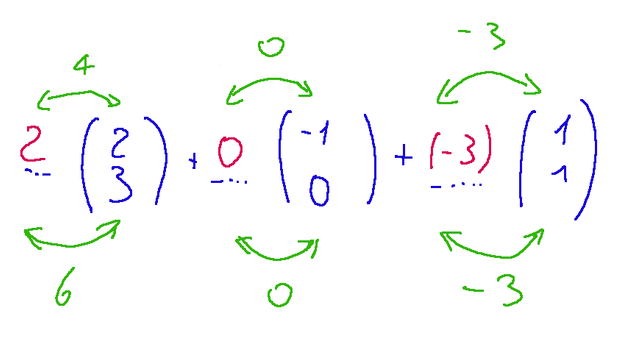
Ed ora eseguiamo le somme dei prodotti

Risultato
Avremo quindi che il vettore risultante da questa combinazione lineare di vettori colonna sarà il seguente.

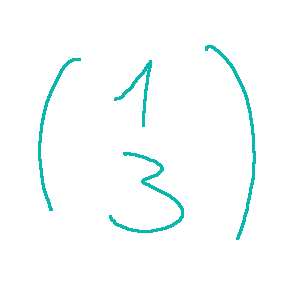
Conclusioni
Le combinazioni lineari di vettori colonna sono un concetto chiave dell'algebra lineare e della geometria analitica. Si tratta di combinare più vettori usando dei numeri scalari per ottenere un nuovo vettore.

Domanda
Le combinazione lineare dei vettori colonna sono un concetto base della geometria analitica o dell'algebra, ma non in tutte le scuole vengono insegnati. Voi vi ricordate di aver studiato a scuola le combinazione lineare dei vettori colonna?

THE END