
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
11-11-2024 - Education - Linear Algebra - Isomorphisms [EN]-[IT]
With this post I would like to provide some brief notions about the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-79)
Isomorphisms
Isomorphisms are invertible linear applications.
Keep in mind that finitely generated vector spaces on the same field with the same dimension are equivalent up to isomorphisms.
In other words we can say that an invertible linear application is called an isomorphism.
An invertible linear application from a vector space into itself is called an automorphism.
To indicate an isomorphism between V and W the following writing is used

If an application
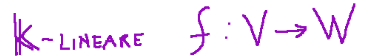
it is invertible, its inverse

And an application

In linear algebra or analytic geometry, an isomorphism between two vector spaces is a particular linear application that "preserves the structure" of these spaces, in the sense that it allows you to move from one space to the other without losing information.
Let's better define what is isomorphism
A linear application
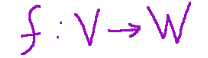
between two vector spaces V and W is called isomorphism if it satisfies two fundamental conditions:
1-Injectivity.
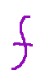
is injective, that is, if
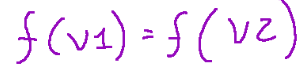
At that time
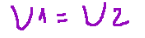
In other words, distinct elements of V are sent to distinct elements of W
2-Surjectivity.
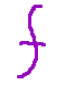
is surjective, that is, every element of W is the image of at least one element of V through f.
Conclusions
We can therefore say that a linear application is an isomorphism if it is a perfect correspondence between V and W, in the sense that to every element of V corresponds one and only one element of W, and vice versa.
If a linear application is both injective and surjective, it is said to be bijective or invertible, and it means that there exists an inverse application

that cancels the effect of f
Question
I find isomorphisms not very easy to understand. Have you ever studied isomorphisms? Did you understand them immediately?

[ITALIAN]
11-11-2024 - Education - Algebra lineare - Isomorfismi [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-79)
Isomorfismi
Gli isomorfismi sono applicazioni lineari invertibili.
Da tenere presente che gli spazi vettoriali finitamente generati sullo stesso campo con la stessa dimensione sono equivalenti a meno di isomorfismi.
In altre parole possiamo dire che un’applicazione lineare invertibile è detta isomorfismo.
Un’applicazione lineare invertibile da uno spazio vettoriale in sé stesso è detta automorfismo.
Per indicare un isomorfismo tra V e W si usa la seguente scrittura

Se un’applicazione
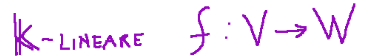
è invertibile, la sua inversa

è un’applicazione

In algebra lineare o in geometria analitica, un isomorfismo tra due spazi vettoriali è una particolare applicazione lineare che "preserva la struttura" di questi spazi, nel senso che permette di passare da uno spazio all'altro senza perdere informazioni.
Definiamo meglio cosa è l’isomorfismo
Un’applicazione lineare
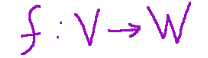
tra due spazi vettoriali V e W si dice isomorfismo se soddisfa due condizioni fondamentali:
1-Iniettività.
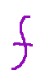
è iniettiva, ovvero, se
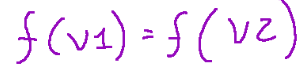
allora
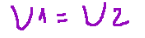
In altre parole, elementi distinti di V sono mandati in elementi distinti di W
2-Suriettività.
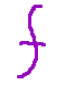
è suriettiva, cioè ogni elemento di W è l’immagine di almeno un elemento di V attraverso f.
Conclusioni
Possiamo quindi dire che, un'applicazione lineare è un isomorfismo se è una corrispondenza perfetta tra V e W, nel senso che ad ogni elemento di V corrisponde uno e un solo elemento di W, e viceversa.
Se un'applicazione lineare è sia iniettiva che suriettiva, si dice che è biunivoca o invertibile, e significa che esiste un'applicazione inversa

che annulla l’effetto di f
Domanda
Ritengo gli isomorfismi poco immediati da capire. Avete mai studiato gli isomorfismi? Li avete compresi immediatamente?
THE END
I have very little idea about this linear algebra, I understand this algebra very little, you have taught us the subject in a very concise and very nice way, very nice to see your post, thanks a lot for sharing this nice post with us.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
These are concepts that, if not well understood, make it difficult to carry out operations or transformations.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Non parlarmi di quell'argomento, per favore. Ho dovuto cercare aiuto. Ho pagato un compagno di classe per insegnarmi fuori dalle lezioni e non potevo permettermi di ripetere materia e non ci sono riuscito perché ho studiato con una borsa di studio che ho vinto all'università.
Ti dico, c'è un bando per persone a basso reddito, c'erano 10 posti, mia madre mi dice di portare tutti i documenti e di avere fede in DIO. Ho vinto la borsa di studio grazie a DIO e ho finito gli studi universitari con una borsa di studio dell'università. Essere in borsa di studio è una grande responsabilità ma mi ha aiutato a essere più disciplinato.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Sei stato bravo e tua madre sarà stata davvero contenta e fiera di te
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Education is actually the key and should not be joked with actually because it plays a very important role in our society in transforming a lot of things positively about our society
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I agree, education has a primary role in any kind of society and culture
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit