~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
28-11-2024 - Education - Linear Algebra - Classification of Conics [EN]-[IT]
With this post I would like to provide some brief notions regarding the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-57)
Classification of Conics
Definition
Conics are a class of plane curves studied in analytical geometry. They are defined as the locus of points that satisfy a certain condition with respect to a fixed point, called focus, and a fixed line, called directrix.
Classification of Conics
quadratic form
The polynomial that defines a conic with a homogeneous equation
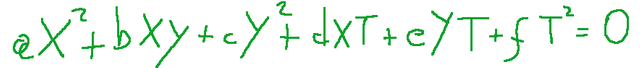
can also be thought of as a quadratic form.
The matrix associated with it is the following
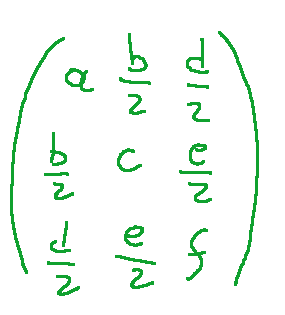
Indeed we have
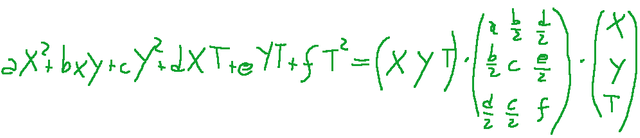
associated matrix
Given a conic C with equation homogeneous
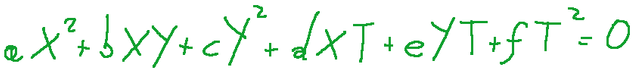
the matrix
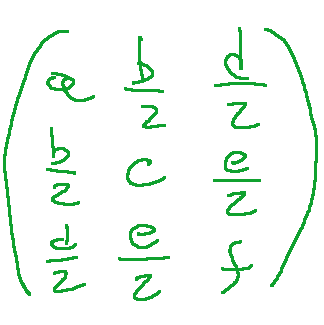
this is called the matrix associated with the conic C
degenerate
A conic with associated matrix A is degenerate if and only if det(A) = 0
The conic C with equation homogeneous
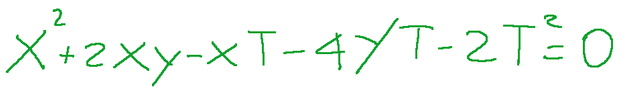
is degenerate, in fact the determinant of the associated matrix
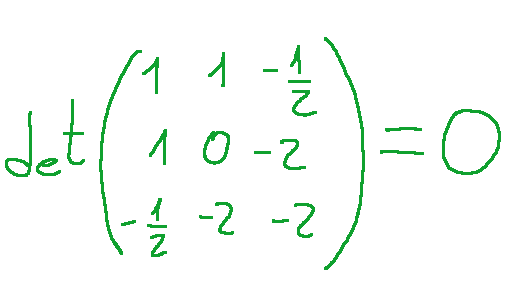
is zero.
Euclidean classification of conics
A non-degenerate conic C with associated matrix A can be represented by one of the following Euclidean canonical forms with an appropriate choice of the Cartesian reference system.
-Real ellipse
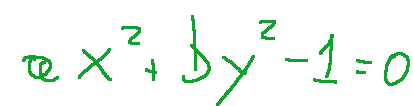
-Ellipse imaginary
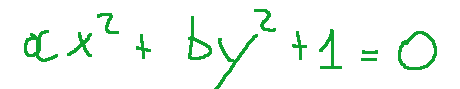
-Hyperbola
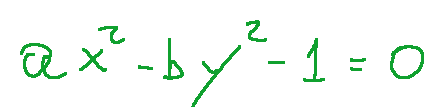
-Parabola
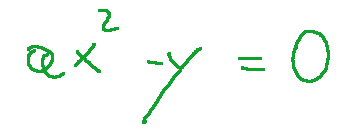
Example exercise
Let's try to classify the conic of equation
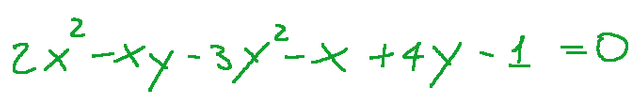
Development
The matrix associated with the conic is
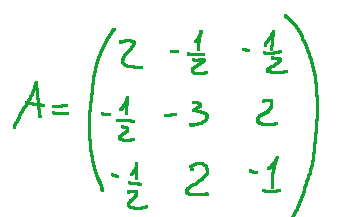
so we have that
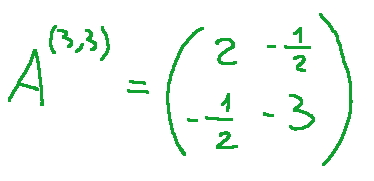
At this point we go to calculate the determinant and we see that det(A)=0. So the determinant is zero and consequently we know that the conic is degenerate.
We also have that rank(A)=2, that is, the rank of the matrix is 2.
We can say that the quadratic form
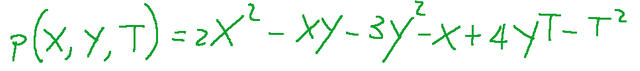
represented by A is undefined.
The conic is a pair of real lines.
Conclusions
The Classification of Conics is a mathematical method that allows us to identify and distinguish between different types of conics, that is, plane curves obtained by intersecting a plane and a right circular cone with two sides. Classification is essential to understand the geometric and algebraic properties of conics, as well as to apply them in different fields of mathematics, such as analytic geometry, mechanics and engineering.
Question
I think this field of mathematics is starting to be difficult to understand. Have you ever tried to classify a conic?

[ITALIAN]
28-11-2024 - Education - Algebra lineare - Classificazione delle coniche [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-57)
Classificazione delle coniche
Definizione
Le coniche sono una classe di curve piane studiate nella geometria analitica. Sono definite come il luogo dei punti che soddisfano una certa condizione rispetto a un punto fisso, detto fuoco, e a una retta fissa, detta direttrice.
Classificazione delle coniche
forma quadratica
Il polinomio che definisce una conica con equazione omogenea
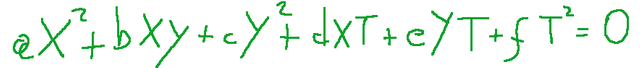
può anche essere pensato come una forma quadratica.
La matrice associata ad essa è la seguente
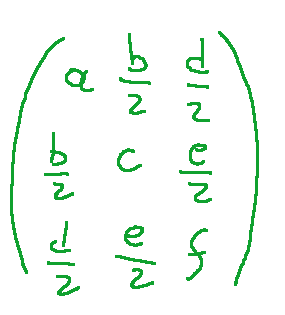
Infatti abbiamo
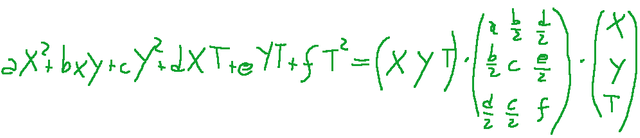
matrice associata
Data una conica C con equazione omogenea
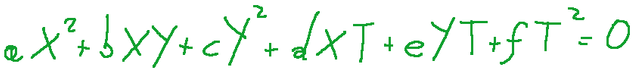
la matrice
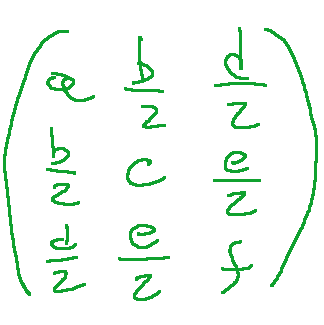
questa è chiamata matrice associata alla conica C
degenere
Una conica con matrice associata A è degenere se e solo se det(A) = 0
La conica C con equazione omogenea
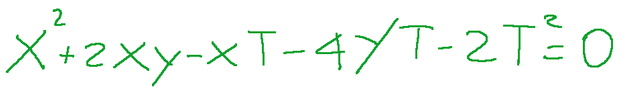
è degenere, infatti il determinante della matrice associata
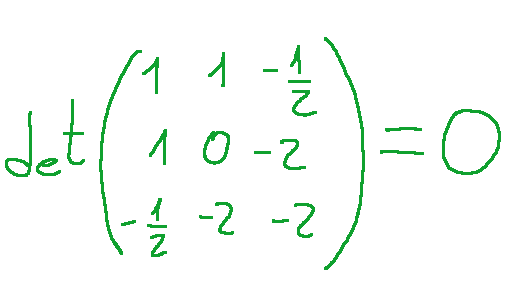
è nullo.
Classificazione euclidea delle coniche
Una conica non degenere C con matrice associata A può essere rappresentata da una delle seguenti forme canoniche euclidee con una scelta opportuna del sistema di riferimento cartesiano.
-Ellisse reale
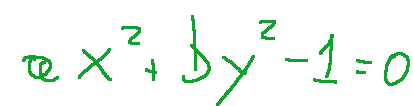
-Ellisse immaginaria
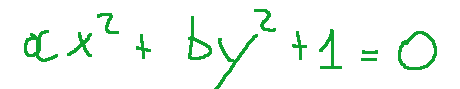
-Iperbole
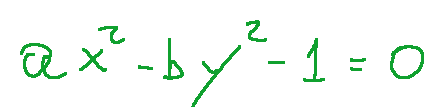
-Parabola
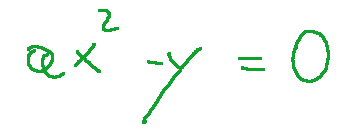
Esempio di esercizio
Proviamo a classificare la conica di equazione
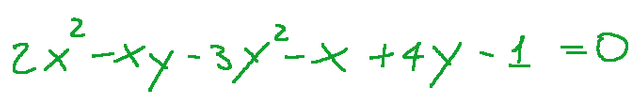
Sviluppo
La matrice associata alla conica è
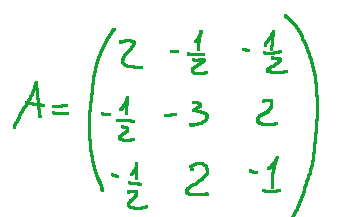
quindi abbiamo che
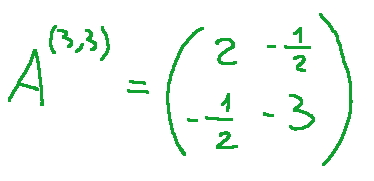
A questo punto andiamo a calcolare il determinante e vediamo che det(A)=0. Quindi il determinante è nullo e di conseguenza sappiamo che la conica è degenere.
Abbiamo inoltre che rank(A)=2, cioè il rango della matrice è 2.
Possiamo dire che la forma quadratica
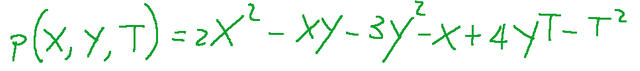
rappresentata da A è indefinita.
La conica è una coppia di rette reali.
Conclusioni
La Classificazione delle coniche è un metodo matematico che consente di identificare e distinguere tra diverse tipologie di coniche, ovvero curve piane ottenute intersecando un piano e un cono circolare retto a due falde. La classificazione è fondamentale per comprendere le proprietà geometriche e algebriche delle coniche, nonché per applicarle in diversi campi della matematica, come la geometria analitica, la meccanica e l’ingegneria.
Domanda
Secondo me questo campo della matematica inizia ad essere difficile da comprendere. Avete mai provato a fare la classificazione di una conica?
THE END