30-11-2024 - Education - Linear Algebra - Centers, Diameters, Axes, Asymptotes [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
30-11-2024 - Education - Linear Algebra - Centers, Diameters, Axes, Asymptotes [EN]-[IT]
With this post I would like to provide some brief notions regarding the technical topic mentioned in the subject.
The context in which we operate is that of analytical geometry or linear algebra
(code notes: MOD-55)

Centers, Diameters, Axes, Asymptotes

Definitions
The Center
Let C be a non-degenerate conic. If the pole of the line at infinity with respect to the conic C is not a point at infinity, it is called the center C.
Example
The center of the ellipse C with homogeneous equation

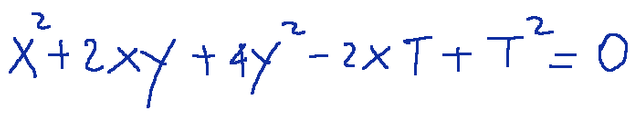
in fact C is the pole of the line at infinity T=0 with respect to the ellipse.

The diameter
Let C be a non-degenerate conic. If the polar line of a point at infinity P with respect to the conic C is not the line at infinity, it is called the diameter of C conjugate to P(infinity), or also to the direction defined by P(infinity)
Example
Let's consider the ellipse with homogeneous equation

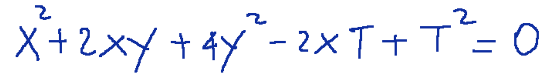
The diameter r of the ellipse with homogeneous equation conjugate to the direction defined by P(infinity) has homogeneous implicit form.
Where:

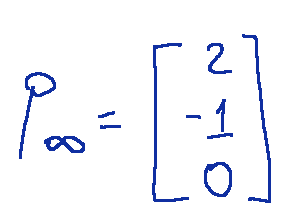
Axis
Let C be a non-degenerate conic. If the diameter of C conjugated to P(infinity) is orthogonal to the direction defined by P(infinity), it is called the axis of C.
The axis of symmetry is a straight line that divides a geometric figure into two mirrored parts. If a figure is reflected with respect to its axis of symmetry, it appears identical to the original figure.
As regards the axis of a conic (ellipse, hyperbola, parabola) we can say that the axis is a significant line linked to their geometry:
-Parabola: The axis is the straight line that passes through the vertex and the focus, perpendicular to the directrix. It is the axis of symmetry of the parabola.
-Ellipse and hyperbola: There are two axes:
Major axis: The line that passes through the foci and the center of the conic; it is the maximum diameter.
Minor axis: The line perpendicular to the major axis that passes through the center; it is the minimum diameter.

Asymptotes
Let C be a non-degenerate conic. If the diameter of C conjugate to a point at infinity P(infinity) contains P(infinity, it is called an asymptote of C).
We can also define the asymptote as follows:
an asymptote is a line that approaches a curve indefinitely but never intersects it (or only at a point infinitely distant). Asymptotes represent the "long-term" behavior of the curve when the x or y coordinates tend to infinity or to minus infinity.
Example
In standard hyperbolas, such as

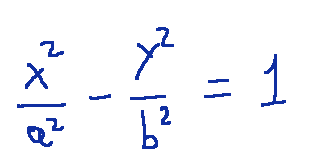
have two asymptotes that intersect the center of the conic and represent the main directions of approach of the branches of the curve.
The asymptotes are given by the equations

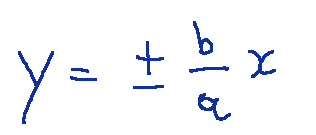
Conclusions
The center is a pivotal point for many geometric figures, such as circles, ellipses and hyperbolas. It represents the central symmetry point of the figure, around which the shape is balanced.
Diameters are significant lines that pass through the center and often connect points of the figure in a symmetrical way.
Axes represent lines of symmetry and reference that structure the geometric figure.
Asymptotes describe the "infinite distance" behavior of non-closed curves, such as the hyperbola, and provide a simplified representation of their growth or tendency.

Question
I remember when I studied centers, diameters, axes and asymptotes in school. Geometrically their explanation is simple, but the algebraic explanation always seemed complex to me, what do you think?

---

---

[ITALIAN]
30-11-2024 - Education - Algebra lineare - Centri, diametri, assi, asintoti [EN]-[IT]
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento tecnico citato in oggetto.
Il contesto in cui operiamo è quello della geometria analitica o algebra lineare
(code notes: MOD-55)

Centri, diametri, assi, asintoti

Definizioni
Il centro
Sia C una conica non degenere. Se il polo della retta all’infinito rispetto alla conica C non è un punto all’infinito, esso è detto centro C.
Esempio
Il centro dell’ellisse C con equazione omogenea

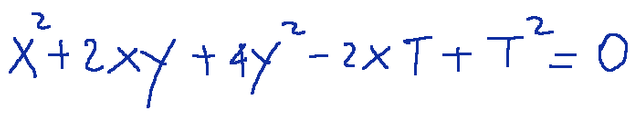
infatti C è il polo della retta all’infinito T=0 rispetto all’ellisse.

Il diametro
Sia C una conica non degenere. Se la retta polare di un punto all’infinito P rispetto alla conica C non è la retta all’infinito, essa è detta diametro di C coniugato a P(infinito), o anche alla direzione definita da P(infinito)
Esempio
Consideriamo l’ellisse con equazione omogenea

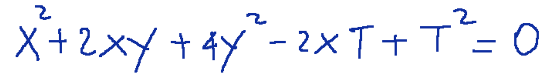
Il diametro r dell’ellisse con equazione omogenea coniugato alla direzione definita da P(infinito) ha forma implicita omogenea.
Dove:

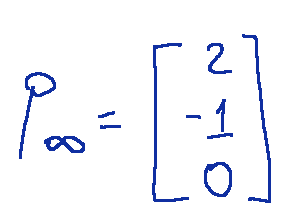
Asse
Sia C una conica non degenere. Se il diametro di C coniugato a P(infinito) è ortogonale alla direzione definita da P(infinito), esso è detto asse di C.
L’asse di simmetria è una retta che divide una figura geometrica in due parti speculari. Se una figura è riflessa rispetto al suo asse di simmetria, appare identica alla figura originale.
Per quanto riguarda l’asse di una conica (ellisse, iperbole, parabola) possiamo dire che l'asse è una linea significativa legata alla loro geometria:
-Parabola: L'asse è la retta che passa per il vertice e il fuoco, perpendicolare alla direttrice. È l'asse di simmetria della parabola.
-Ellisse e iperbole: Esistono due assi:
Asse maggiore: La retta che attraversa i fuochi e il centro della conica; è il diametro massimo.
Asse minore: La retta perpendicolare all'asse maggiore che passa per il centro; è il diametro minimo.

Asintoti
Sia C una conica non degenere. Se il diametro di C coniugato a un punto all’infinito P(infinito) contiene P(infinito, esso è detto asintoto di C).
Possiamo definire l’asintoto anche come segue:
un asintoto è una retta che si avvicina indefinitamente a una curva ma non la interseca mai (o lo fa solo in un punto a distanza infinita). Gli asintoti rappresentano il comportamento "a lungo termine" della curva quando le coordinate x o y tendono a infinito o a meno infinito.
Esempio
Nelle iperboli standard, come

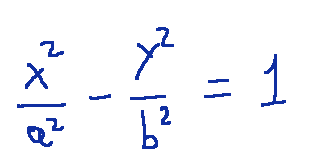
hanno due asintoti che intersecano il centro della conica e rappresentano le direzioni principali di avvicinamento dei rami della curva.
Gli asintoti sono dati dalle equazioni

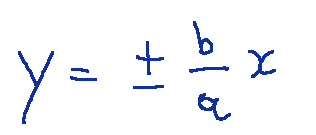
Conclusioni
Il centro è un punto cardine per molte figure geometriche, come circonferenze, ellissi e iperboli. Esso rappresenta il punto di simmetria centrale della figura, attorno al quale la forma è bilanciata.
I diametri sono rette significative che attraversano il centro e spesso collegano punti della figura in modo simmetrico.
Gli assi rappresentano linee di simmetria e riferimento che strutturano la figura geometrica.
Gli asintoti descrivono il comportamento "a distanza infinita" delle curve non chiuse, come l’iperbole, e forniscono una rappresentazione semplificata della loro crescita o tendenza.

Domanda
Ricordo quando a scuola ho studiato i centri, i diametri, gli assi e gli asintoti. Geometricamente la loro spiegazione è semplice, ma la spiegazione algebrica mi è sempre sembrata complessa, voi che ne pensate?

THE END