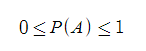1.
우리 생활에 확률이 안쓰이는 곳이 없다
자주 하는 컴퓨터 게임에서도, 친구들과의 내기에서도
하물며 티비에서 나오는 일기예보에서도 확률은 쓰인다
이런 확률의 고전적 정의는 2와 같다
1-1.
시행 : 무수히 반복가능하며 조건에 따라 서로 다른 결과를 나타내는 실험
결정적실험(deterministic experiment): 실험을 할 때 특정 조건에 띠라 동일한 결과가 나오는 경우
확률실험(random experiment) : 동일한 조건으로 실험을 하더라도 서로 다른 결과가 나오는 경우
표본 공간(sample space): 확률실험에서 모든 가능한 결과의 집합, Ω또는 S로 표시
근원사건(elementary event): 표본공간의 원소
사건, 사상(event): 관심있는 결과의 집합, 표본공간의 부분집합, A,B,...등으로 표시
사건 A가 일어날 확률: P(A)로 표시, 여기서 P를 확률함수 또는 확률라고 한다.
2.
결과가 여러개이고, 각각의 결과가 나올 가능성이 동일할 경우
사건 A가 발생할 확률 P(A)의 값은 아래와 같다
3.
예시를 들어보자
당신이 동전을 하나 가지고 있다
동전을 튕겼을 때 발생할 사건은 (꼿꼿이 서는 경우를 제외하면) 앞, 뒤라는 사건이다
그러면 동전이 앞면일 확률 P(앞)은
4.
당신이 주사위를 가지고 있다
주사위를 굴렸을 때 발생할 사건은 1,2,...,6이다
그러면 주사위를 굴렸을 때 6이 나올 확률은
4보다 작은 수가 나올 확률은
5.
확률의 기본 성질은 아래와 같다
(1) 임의의 사건 A에 대하여
(2) 반드시 일어나는 사건 S에 대하여 P(S) = 1
(3) 반드시 일어나지 않는 사건 Ø에 대하여 P(Ø) = 0