

From the Author:
Salutations.
I am JaiChai.
And if I haven't had the pleasure of meeting you before, I'm delighted to make your acquaintance now.

I invite you to interact with everyone, learn, and have as much fun as possible!
For my returning online friends, "It's always great to see you again!"
What is λ-calculus?
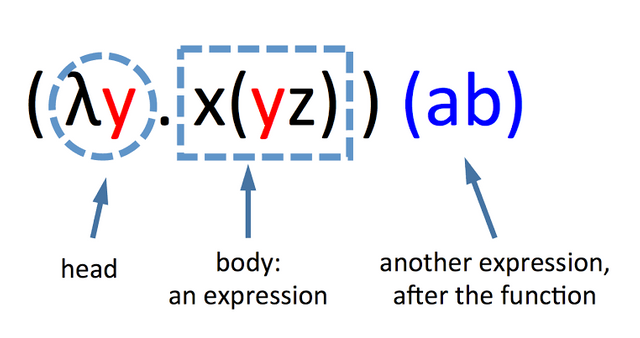
Lambda calculus (also written as λ-calculus) is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution.
Okay, so what?
And why am I bothering to learn it?
Well, here’s 5 reasons:
1. λ-calculus can Encode ANYTHING.

In the 1930’s, Prof. Alonzo Church was, like many mathematicians of his day, exploring the foundations of mathematics and invented the λ-calculus.
Church was the Ph.D. Supervisor for Alan Turing, the man who cracked the Nazi's Enigma Machine during WWII and advanced Computer Science by light years with his "Turing Machine" - a machine capable of encoding ANYTHING.
Church’s λ-calculus proved to be able to encode ANYTHING too (albeit using a very different method).
Here's my crude explanation of the major differences between the two models of computation:
Turing used Boolean Logic and a state-based model.
Church used λ-calculus and functions for his state-less model.
The “Church-Turing Hypothesis" says that they are computationally equal and can ENCODE ANYTHING".
Why was this a game-changer?
For the scientists, moreso for the mathematicians of the '30s and '40s, the ability to encode anything; that is, to represent and define whatever you desire according to clear, established (or agreed upon) syntax and semantics, drastically increases the speed and depth of shared knowledge and understanding for all involved; while diminishing common errors caused by ambiguity within the group.
For the rest of Humanity, the most significant outcome from this all-inclusive encoding is the giant leap in both the breadth and depth of human-machine and machine-human communication - using a shared syntax and semantic structure (translated: a language that they both can understand and use).
2. λ-calculus is the foundation for ALL Functional Programming.

ALL Functional Programming Languages – FPL (e.g., Haskell, the ML Group, LISP, Scala, etc.) are based on λ-calculus.
Several popular non-FPL programming languages, such as Python, Java, JavaScript, Ruby, C++ and many others, have now incorporated quite a few λ-calculus based functions into their code base.
Originally, I began learning λ-calculus because I was teaching myself an FPL called Haskell at the time.
But now, I have several more reasons for learning λ-calculus.
3. λ-calculus requires a major paradigm shift and develops an increasing understanding of Higher Levels of Abstraction.
Levels of Abstraction -
The level of abstraction is the amount of complexity by which a system is viewed or programmed.
The higher the level, the less detail. The lower the level, the more detail.
The highest level of abstraction is the entire system.
The next level would be a handful of components, and so on, while the lowest level could be millions of objects.
Source
Why understanding Higher Levels of Abstraction is Important for everyone -
Humans use abstraction layers in everyday life.
...A door lock provides an abstraction that simplifies our ability to restrict access to a room.
Even people, who do not know how such a device is implemented, can understand its purpose and can make use of it.
Simply put, whether it's an activity of daily life or designing a computer program, the level of abstraction affects everything (e.g., the size of scope, granularity of detail, degrees of effectiveness, operating ranges, standards of efficiency, etc.) that contributes to or undermines a successful outcome.
Understanding higher levels of abstraction provides higher vantage points for observation and elicits a deeper understanding of how things, especially complex systems, are designed, constructed, and behave/operate/function under varying conditions.
The higher the level of abstraction understood, the more things are contained within or "under the umbrella" of that abstraction; enabling that person to learn more things, with less difficulty and at a faster pace than a person at a lower level of abstraction comprehension.
Stated differently, the higher the level of abstraction comprehension, the easier it is to flatten out the steep learning curves of new, so-called "hard subjects".
A quick note before moving forward -
I almost relegated reasons 4. and 5. to be subordinate elements of reasons 1., 2. and 3.
Later, I decided that reasons 4. and 5. deserved a little ink, a short write-up explaining their significance - no matter how interconnected they are to the previously listed reasons.
With that said, let's charge on.
4. λ-calculus helps me understand Deep Learning better.

Deep learning is an AI function that mimics the workings of the human brain in processing data for use in detecting objects, recognizing speech, translating languages, and making decisions.
Deep learning AI is able to learn without human supervision, drawing from data that is both unstructured and unlabeled.
Deep Learning; especially how to create an AI from scratch, is another topic that fascinates me and wish to understand better.
λ-calculus helps me achieve this goal in two very concrete ways:
Develops High Level Abstraction Comprehension, a must for understanding Deep Learning.
λ-calculus based FPLs have become the de facto (standalone or partner) programming tools for designing, programming and running Deep Learning Systems.
5. λ-calculus makes it easier to learn Quantum Computer Programming.

Quantum Physics and Quantum Computing are subjects I have been studying for quite awhile.
Quantum Processing will require more and more competent Quantum Computer Programmers - those who can write high-assurance, mission critical code that best exploits the unique and ever-increasing capabilities of Quantum Computing.
From upgrading Cryptographic algorithms and safeguarding Cryptocurrency from a Shor's algorithm attack to modeling extremely complex systems (e.g., weather, economies, molecular biochemistry, etc.) and improving AI accuracy, success or failure will largely depend on the level of expertise and quality of code written by Quantum Computer Programmers.
Similar to reason 4., learning λ-calculus:
Broadens High Level Abstraction Comprehension required to understand many core concepts of quantum physics theory and paradigms used in quantum computational design.
λ-calculus based FPLs have become the de facto standalone or partner programming tools for designing, programming and running quantum simulations.
Question to Ponder:
Do you think learning λ-calculus could benefit you in any way?
I'd love to read your opinions.
By JaiChai
And if you liked my post, kindly Upvote, Comment, Follow, and ReSteem.
About the Author:
.jpg)
Believing that school was too boring, he dropped out of High School early; only to earn an AA, BS and MBA in less than 4 years much later in life – while working full-time as a Navy/Marine Corps Medic.
In spite of a fear of heights and deep water, he performed high altitude, free-fall parachute jumps and hazardous diving ops in deep, open ocean water.

After 24 years of active duty, he retired in Asia.
Since then, he's been a full-time, single papa and actively pursuing his varied passions (Writing, Disruptive Technology, Computer Science and Cryptocurrency - plus more hobbies too boring or bizarre for most folk).
He lives on an island paradise with his girlfriend, teenage daughter and two dogs.
