Il concetto di infinito è qualcosa che possediamo a livello inconscio, ma quando iniziamo a ragionarci su iniziano i problemi. Che cos'è l'infinito? I numeri pari sono la metà dei numeri interi? Esiste l'infinito nel mondo reale?
L'infinito non è un grande numero. No no, è più un concetto. Darne una definizione intuitiva è complicato, perchè è difficile descriverlo senza usare la parola "infinito" o concetti che richiamano ad esso. "l'infinito è ciò che non ha fine" "30 e lode."
Per affrontare il problema dobbiamo parlare di insiemistica, e chiederci: quando due insiemi hanno lo stesso numero di elementi?
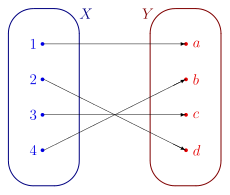
Se in un sacchetto ho quattro mele e nell'altro quattro arance, intuitivamente so che nei due sacchetti c'è lo stesso numero di oggetti. Come si può esprimere questo concetto matematicamente? Si può dire che esiste una correlazione biunivoca tra gli elementi dei due sacchetti, ovvero, posso mettere in relazione una mela con un arancia, e ripetere la stessa operazione con gli altri elementi.
Imagine CC0 Creative Commons
Se posso fare questo allora si dice che gli insiemi hanno lo stesso numero di elementi.
Uno degli scienziati passati alla storia che si interessò al problema dell'infinito è Galileo, tra un processo e l'altro per passare il tempo. Galileo trovò un apparente paradosso nel concetto di infinito, ragionando nel seguente modo.
Supponiamo prendere tutti i numeri interi positivi: 1, 2, 3...e di associare ad essi il loro quadrato, in questo modo:

Immagine dell'autore
Abbiamo costruito due elenchi senza fine di numeri, e ogni elemento della lista di destra è associato a un elemento della lista di sinistra. Ma c'è un problema: i numeri che compaiono nella lista di destra compaiono anche nella lista di sinistra, che però ne contiene anche altri in più. Saremmo istintivamente portati a pensare che nella lista di sinistra ci siano più elementi. Ma questo non è corretto, perchè è sempre possibile mettere in relazione biunivoca gli elementi dei due insiemi. Per ogni elemento della lista di sinistra ci sarà sempre un elemento della lista di destra, e si può continuare senza fermarsi mai. Discorso analogo si può fare per i numeri pari. I numeri sono infiniti perchè, preso l'insieme che li contiene tutti, è possibile trovarne un sottoinsieme i cui elementi possono essere messi in relazione biunivoca con gli elementi dell'insieme totale, ed è quello che abbiamo appena fatto. Questa è una possibile definizione di insieme infinito.
Allora dobbiamo concludere
- che gli insiemi fino ad ora presentati hanno lo stesso numero di elementi,
- che l'infinito è un concetto strano, che sfugge alla logica comune.
Ovviamente gli infiniti non sono tutti uguali. Ci sono infiniti più grandi di altri. Ovvio, no?
Il primo che diede una dimostrazione del fatto che esistono insiemi infiniti più grandi di altri è stato George Cantor, verso la fine del secolo scorso. Cantor ha dimostrato che l'insieme dei numeri reali contiene infinitamente più numeri dell'insieme dei numeri razionali.
- I numeri razionali sono tutti i numeri esprimibili mediante una frazione di numeri interi: 1, 2, 34/75, 1237/454...
- I numeri reali sono i numeri razionali più i numeri non esprimibili sotto forma di frazione, come π.
Innanzitutto, per comprendere meglio la dimostrazione, bisogna mostrare che l'insieme dei numeri razionali contiene lo stesso numero di elementi dei numeri naturali. Il trucco è cercare un modo intelligente per ordinare le frazioni, e Cantor lo fece così:

Immagine dell'autore
Nella prima riga c'è un solo elemento, e la somma delle cifre della frazione fa 2. Nella seconda riga scriviamo tutte le frazioni la cui somma delle cifre al numeratore e al denominatore fa 3. E così via...
In questo modo abbiamo un elenco ordinato di elementi, e possiamo associare un numero naturale ad ognuno di essi.
Ora vediamo come non è possibile fare la stessa cosa con i numeri reali. Consideriamo i numeri compresi nell'intervallo [0 1], e associamo ad ognuno di essi un numero naturale:

Immagine dell'autore
Ora prendiamo la prima cifra decimale del primo numero, la seconda cifra del secondo numero e cosi via, e usiamole per generare un nuovo numero decimale: 0.273292... Aggiungiamo ora 1 a ogni cifra del numero (eccetto lo zero a sinistra della virgola). Nel nostro caso otteniamo 0.384403... Il numero così ottenuto è certamente compreso tra 0 e 1, ma ha una caratteristica peculiare: non può comparire in nessun punto dell'elenco originario di numeri decimali, infatti differisce da ogni numero nell'elenco per almeno una cifra, perchè abbiamo adottato uno specifico criterio per scriverlo ( aggiunto +1 alle cifre).
Ecco dimostrato che l'insieme infinito nei numeri reali è più grande dell'insieme infinito dei numeri naturali. È un infinito di ordine superiore. Un gran bel lavoro di Cantor. Tra l'altro dimostrò anche che esistono infiniti ordini di infinito infinitamente più grandi di altri. Beh...insomma non c'è un infinito in assoluto più grande di tutti, non c'è un universo che contiene altri universi.
Il paradosso dell'albergo infinito di Hilbert fa ben capire quanto siano strani gli infiniti, lo presento brevemente.
In un albergo ci sono infinite stanze, tutte occupate. Se arriva un altro ospite, è possibile dargli una sistemazione? Ma certo, è sufficiente liberare la stanza numero 1 facendo spostare il suo occupante nella numero 2. E quello della numero 2 nella numero 3, e così via, all'infinito. Tutti saranno sistemati, e nessuno avrà nulla da obbiettare.
Tutto questo nel magico mondo della matematica. Ma nel mondo reale?
Oltre al costo infinito, un albergo infinito necessiterebbe di uno spazio infinito in cui stare, ma anche di infinito cibo ed energia per funzionare. Naturalmente il proprietario avrebbe infinite spese, ma altrettanti infiniti guadagni.
Quindi alla fine ci guadagna?
Beh, infinito + infinito = infinito.
Ma, infinito - infinito=...? È una forma indeterminata. Mica detto che ci guadagni.

Imagine CC0 Creative Commons
È chiaramente una situazione assurda. Gli infiniti nel mondo reale non sono ben visti da ingegneri e fisici, anzi. Sono un campanello d'allarme che segnala che qualcosa non va nella teoria che si sta utilizzando per descrivere il fenomeno. Una quantità infinita, che non finisce, che senso ha?
Avete presente i boom sonici no? Quel rumore fortissimo che si produce quando un aereo oltrepassa la velocità del suono nell'aria. Ebbene, le equazioni che descrivono il comportamento dell'aria durante il fenomeno prevedono che la pressione raggiunga valori infiniti. Ovviamente questo non succede, perchè le proprietà del sistema cambiano all'aumentare della velocità, e quelle equazioni non sono più valide oltre un certo limite.

Imagine C00 Creative Commons
Le equazioni dell'elettromagnetismo classico prevedono che un corpo nero emetta una quantità infinita di energia. Cosa falsa, anche perchè in caso contrario l'universo sarebbe incenerito. Una discrepanza così forte tra teoria e realtà ha dato il via alla nascita della meccanica quantistica. C'è però un campo in cui l'esistenza di un infinito fisico è ancora dibattuta. L'Universo. È finito o infinito? Ad oggi non c'è una risposta.
Ma ipotizziamo per un attimo che si infinito. Allora esiste una possibilità non nulla, che a una certa distanza da noi, esista la copia esatta della Terra e di tutti i suoi abitanti. In fondo, se l'universo è infinito prima o poi capiterà che atomi e molecole siano assemblati nello stesso modo.
Siamo nella pura speculazione, beninteso. L'infinito (se c'è) è là dove non possiamo arrivare, ma poco importa. Vale comunque la pena di interrogarsi su cosa sia, e, volenti o nolenti, per comprendere l'Universo dobbiamo scontrarci con esso.
Fonti:
- John Barrow - L'infinito
- www.dm.uniba.it/ipertesto/logici/finito.doc
- http://adl.stanford.edu/aa210b/Lecture_Notes_files/AIAA-1989-1105-891.pdf

Immagine CC0 Creative Commons, si ringrazia @mrazura per il logo ITASTEM.
CLICK HERE AND VOTE FOR DAVINCI.WITNESS

Bravo Roberto!!!
Articoli sempre completi e ben fatti.
Complimenti!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Grazie ;)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi @rscalabrini!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Articolo semplicemente affascinante!
Ed è stupendo riuscire a trovare queste piccole perle di cultura all'interno della community italiana di steemit.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit