Ciao a tutti!
Sicuramente vi è capitato, qualche volta di fare delle votazioni, tra amici, compagni di classe, per votare il sindaco, per decidere dove andare, cosa mangiare, ecc..
E quasi sicuramente, non tutti eravate d'accordo, e bisognava decidere cosa fare, quindi si faceva una votazione.
Ma che metodo di votazione fare? Sarà quello giusto?
Il metodo più ragionevole è quello di andare per maggioranza, facciamo un esempio:
| --> | Numero voti |
|---|---|
| pizza | 11 |
| panino | 9 |
In questo caso ci sono 20 amici che devono decidere se andare a mangiare la pizza o il panino, per la decisione è stato usato il metodo della "Maggioranza semplice". Cioè chi ha più voti vince. In questo esempio la pizza ha ottenuto 11 voti e il panino 9, di conseguenza vince la pizza (meno male).
Cosa succede se si aggiunge una terza alternativa?
Facciamo un esempio:
| --> | Numero voti |
|---|---|
| pizza | 8 |
| panino | 5 |
| Kebab | 7 |
In questo caso ci sono sempre 20 "elettori" ma le scelte diventano 3! Che fare? Proviamo con il nostro solito metodo e vediamo che la pizza ottiene 8 voti, il kebab 7 e il panino 5. Vince per maggioranza la pizza accontentando 8 persone e scartando le altre 12 che avevano votato altro.
Ok, ma esistono altri sistemi di voto?
La risposta è sì. Infatti il matematico francese Jean-Charles de Borda nel 1770 formalizzò un suo sistema di voto "ponderato".
Questo sistema è ancora utilizzato oggi per attribuire premi sportivi e anche per le elezioni parlamentari in alcuni paesi.
Procedimento:
Si prende un numero n che deve essere minore o uguale al numero dei candidati e ogni elettore deve fare una lista in base alle sue preferenze, la persona che occuperà il primo posto è quella che ritiene più idonea al ruolo e l'ultima è la peggiore.
Facciamo un esempio:
| Elettore A | Luca | Matteo | Giorgia | Maria |
| Elettore B | Luca | Maria | Giorgia | Matteo |
| elettore C | Matteo | Maria | Luca | Giorgia |
| Elettore D | Giorgia | Maria | Luca | Matteo |
| Elettore E | Maria | Giorgia | Matteo | Luca |
In questo caso 5 elettori dovevano decidere chi eleggere come rappresentante:
Luca è stato scelto come prima opzione da 2 persone, Maria, Giorgia e Matteo da una persona ciascuno, utilizzando il sistema della maggioranza il vincitore è naturalmente Luca.
Ma sentiamo cosa dice De Borda, infatti per cercare il migliore candidato bisogna dare un punteggio ad ogni voto, dove al primo della lista dell'elettore si attribuiscono n punti, al secondo n-1, al terzo n-2, ecc...
In questo caso vediamo cosa succede:
| Luca | 2x4+2x2+1 | 13 |
| Maria | 4+3x3+1 | 14 |
| Matteo | 4+3+2+1 | 10 |
| Giorgia | 4+3+2x2 | 11 |
Wow in questo caso il vincitore non è Luca, ma Maria!
Infatti tre quinti delle persone hanno scelto Maria come seconda preferita, ritenendola migliore di Luca.
E' bastato cambiare sistema di voto per far eleggere una persona diversa, questo fa riflettere, e molto.
Se questa persona fosse stata un presidente? O un qualsiasi personaggio importante?
Difetti di questo metodo
Purtroppo questo metodo ha diversi problemi:
- Può capitare che 2 persone abbiamo lo stesso punteggio
- Questo metodo spinge a fare dei voti "tattici", infatti qualcuno potrebbe piazzare il candidato avversario in ultima posizione solo per farlo perdere senza seguire la preferenza ideale.
Esistono diverse versioni di questo sistema, ma ognuna presenta i suoi pro e contro.
Altri metodi
Nello stesso periodo il matematico Condorcet, rivale di de Broda, pensò ad un nuovo sistema di voto, ma questo matematico è più famoso per il suo paradosso: Il paradosso si Condorcet
Ecco un esempio:
| Luca | 2x4+2x2+1 | 13 |
| Maria | 4+3x3+1 | 14 |
| Matteo | 4+3+2+1 | 10 |
| Giorgia | 4+3+2x2 | 11 |
In questo caso i 3 amici hanno idee completamente diverse, e con qualsiasi metodo di voto non ci sarà nessun vincitore.
Condorcet a questo punto decise di creare un sistema di voto composto da "duelli", dove ogni proposta viene comparata con un'altra, e in base al numero di vittorie si decide il "vincitore di Condorcet" cioè la proposta migliore.
In questo modo potrebbe vincere anche la proposta che non è stata scelta da nessuno come prima preferenza, ma quella che è la meno sgradita da tutti.
Questo metodo, però, è molto lungo e venne anche molto criticato nel passato.
Un economista geniale: Arrow
Arrow già da giovanissimo era un genio della matematica, e cercava un argomento interessante per la sua tesi di dottorato, PERSE 8 mesi per cercare l'argomento adatto, fino a quando entrò in un bar e vide che degli uomini stavano discutendo sulle votazioni, Arrow a questo punto capì che quello sarebbe stato il suo argomento.
Se la geometria euclidea è basata su 10 assiomi, perché non fare la stessa cosa con i sistemi di voto?
Per chi non è pratico di matematica, ecco la definizione di assioma:
"In matematica si chiamano postulati o assiomi tutti e soli gli enunciati che, pur non essendo stati dimostrati, sono considerati veri."
Ecco i quattro assiomi che Arrow portò nella sua tesi:
- Universalità: il risultato deve essere univoco, senza pareggi tra i candidati.
- Democraticità = Anonimato: il risultato non deve dipendere solo dalle scelte di un singolo votante oppure di un sottoinsieme dei votanti, ignorando gli altri.
- Unanimità: se tutti i votanti preferiscono la scelta A alla scelta B, anche la graduatoria finale vedrà A precedere B.
- Indipendenza dalle alternative irrilevanti: se un candidato si ritira, la nuova graduatoria deve essere la stessa di quella vecchia a meno naturalmente della presenza di quel candidato.
A questo punto se ci sono tre o più candidati e due elettori questi vincoli sono incompatibili e quindi non esiste nessuna graduatoria (complessiva) che rispetti tutti questi assiomi.
Questo è il famoso "Teorema di Arrow" , dove Arrow giunge ad affermare che è impossibile trovare una funzione per il benessere sociale, escludendo la presenza di un dittatore e la negazione degli assiomi.
Ma perché tutti questi problemi? Cenni storici.
Torniamo indietro negli anni 2000, (io me lo ricordo molto bene XD), quando ci furono le elezioni presidenziali degli Stati Uniti d'America.
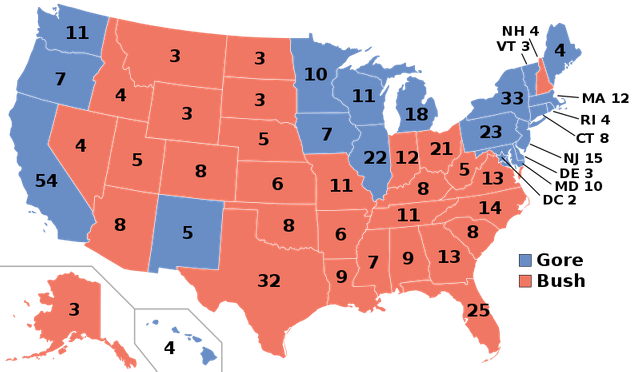
La sfida era tra il Repubblicano Bush e il democratico Al Gore, sappiamo tutti che (purtroppo?) vinse Bush, ma guardiamo bene i dati:
| Presidente | Grandi elettori | Voti | Percentuale |
| Bush | 271 | 50 456 002 | 47,9 |
| Al Gore | 266 | 50 999 897 | 48,4 |
Wow molte più persone avevano votato per Al Gore, esattamente 543.895 persone in più, ma allora perché è stato eletto Bush? Negli Stati uniti i cittadini non votano i presidenti, ma votano i grandi elettori che andranno a votare i presidenti, e grazie a questo metodo Bush vinse le elezioni, se ci pensiamo bene questo fatto delle votazioni è un bel po' importante! Perché il presidente degli Stati Uniti è forse la persona più importante del mondo, e può decidere le sorti di tutti noi. Questo fa riflettere, non poco, non si parla di andare a mangiare la pizza o il gelato.
Conclusioni
Per concludere voglio lasciarvi questa frase di George Szpiro:
I paradossi sono inevitabili e ogni meccanismo di voto presenta delle incongruenze e può essere manipolato. Salvo uno, certo, ma si chiama dittatura.
Delusi? Lo sono anche io, dopo tante ricerche, arrivare a questo punto mi ha lasciato un po' amareggiato.
Grazie per aver letto fino a questo punto!! Voi cosa ne pensate??
Fonti e approfondimenti
- https://www.focus.it/scienza/scienze/la-democrazia-matematicamente-impossibile-9876-1345
- http://www.bollatiboringhieri.it/libri/george-g-szpiro-la-matematica-della-democrazia-9788833923864/
- http://www.science.unitn.it/probab/Mathmodels/elezioni2.pdf
- http://www.raistoria.rai.it/articoli/bush-vince-su-gore-per-una-manciata-di-voti/11538/default.aspx

Il tuo post è stupendo, affronta un argomento che tocca la vita di tutti noi parlandone da un punto di vista teorico-matematico molto interessante. Molti nemmeno sanno dell'esistenza di voti diversi dalla "maggioranza semplice": hai fatto affiorare tutta la complessità delle scelte multiple e ponderate. Ho apprezzato tantissimo anche l'excursus storico e la presenza chiarificatrice di esempi semplici e di immediata comprensione. La democrazia è davvero difficile fin dalle sue basi.
In fondo una bella dittatura risolve tante cose X-/
Una domanda: Perché Arrow escluse la possibilità di una funzione per il benessere sociale? Non mi è chiaro.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Grazie mille! Sono contento che ti sia piaciuto!
Arrow fece diverse dimostrazioni e capì che non era possibile trovare un sistema di voto perfetto, seguendo i suoi 4 assiomi.
Se sei curioso ecco un link dove viene spiegato tutto con diversi esempi:
http://leganerd.com/2012/03/27/la-democrazia-impossibile-arrow-borda-e-condorcet/
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Wow, grazie per il link, adesso é più chiaro!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Greetings @siack! Your post was chosen at random and was resteemed as part of Shareables' campaign. Enjoy your free resteem!
@Shareables, we resteem anything we find shareable. Always strive for quality content. Go on express and harness your blogging potential!
God bless from us @Shareables!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Da wikipedia
E' matematicamente provato che il popolo non avrà mai il potere!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Ahah esatto, speriamo in futuro.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Interessante
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Grazie mille.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Interessante
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Grazie.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @sciack! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last announcement from @steemitboard!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit