Maths is Life! - Extraneous Solutions

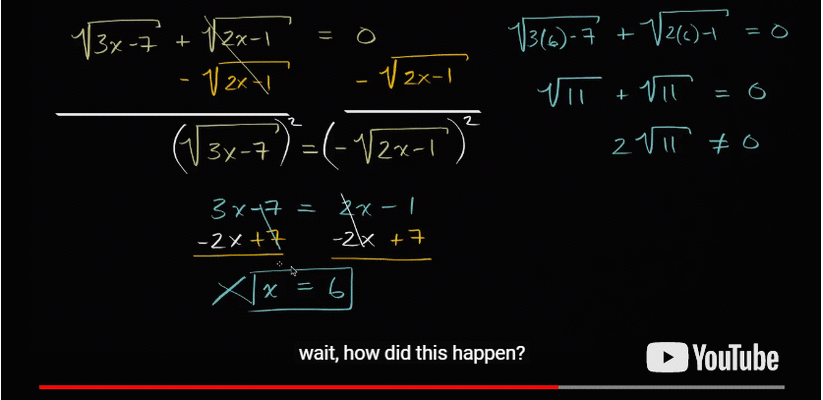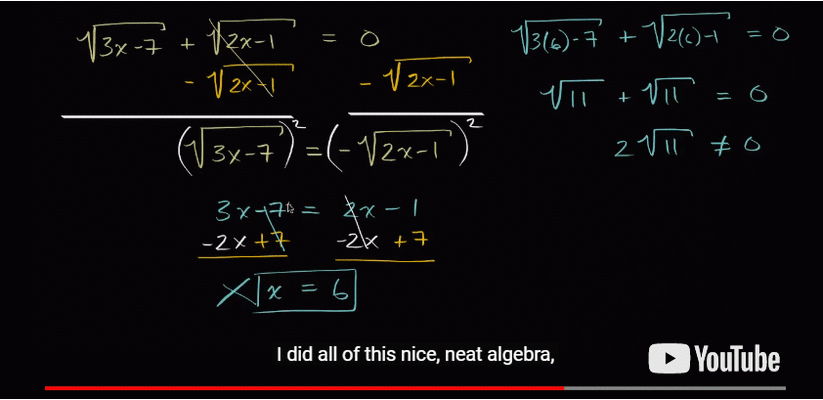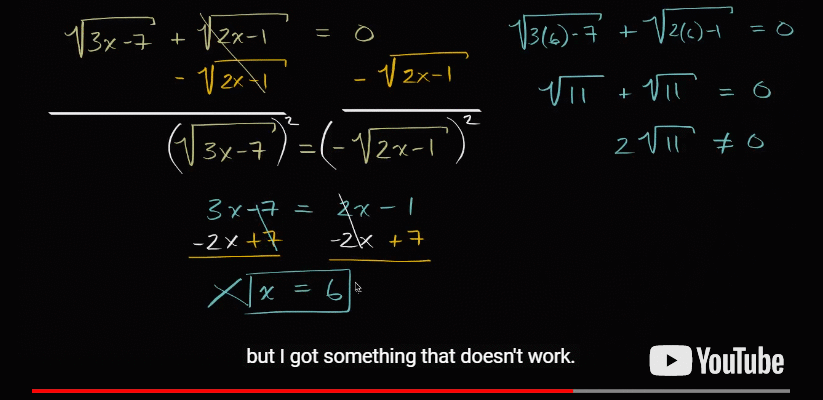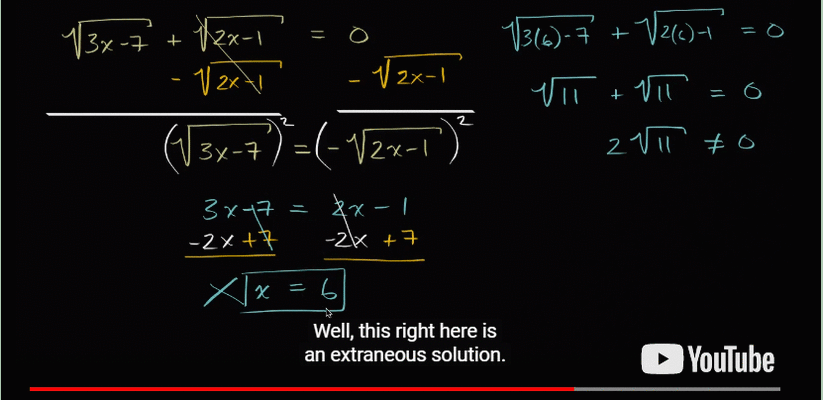
In political debate these days, everyone is so sure of themselves. Not only are people not able to see the other side, they see the other side as monsters or criminals.

When you've worked a problem through logically, checked all your working, made sure it's all correct, how can you possibly be wrong.

Well, even in something as well defined as mathematics, you can go through all the steps correctly and still be wrong! The problem is laid out in the gif above.

If you don't understand what is going on there, I'll try to explain. We start with a problem where we have two square roots and we need to work out what x is for the equation to work out. Using correct algebraic rules in each step, we get to the answer, x=6.

But when we substitute 6 for x in the original equation, it doesn't work! What we've ended up with is the solution to a similar equation, but not the one we started with.

If this is easy to do in math, just think how easy it is to do in arguments. Assumptions creep in unnoticed and we just keep working away, obliviously, to an extraneous, or incorrect, solution.

So next time you're angry with someone for disagreeing with you, even though you've logically worked your way through the issue, spare a thought for the extraneous solution. The solution you arrived at correctly, but still doesn't answer the original problem.

!originalworks