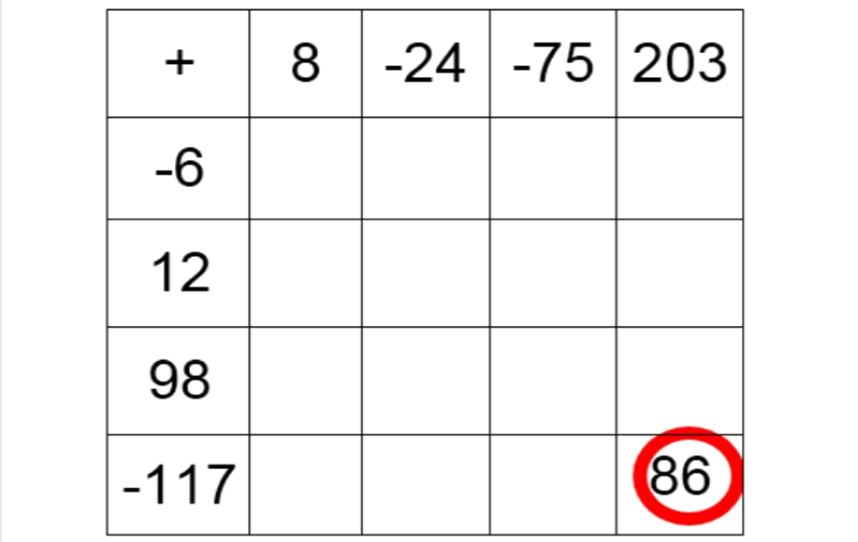Actualizado en el siguiente post
Adición en Z
Comenzar a trabajar con el conjunto Z, genera en los estudiantes un cambio brusco. Debido a que durante años ellos desconocían la existencia de los números que se encuentran antes del cero. Se les hace difícil comprender que por ejemplo a 5 se le pueda restar 11. La comprensión de la regla de los signos para la adición de números Enteros, es el objetivo principal de esta publicación.
Antes de iniciar el tema debemos recordar que el conjunto Z (Conjunto de números Enteros) está conformado por los números positivos y negativos. Desde el menos infinito, pasando por el cero, hasta llegar al infinito positivo. Dichos números pueden sumarse, restarse, multiplicarse y dividirse al igual que los números naturales.
Regla de los signos para la adición de números Enteros
Signos IGUALES se SUMAN y se conserva el signo
Signos DISTINTOS se RESTAN y se coloca el signo del número con mayor valor absoluto.

Caso 1: Cuando ambos números son positivos
Signos IGUALES se SUMAN y se conserva el signo
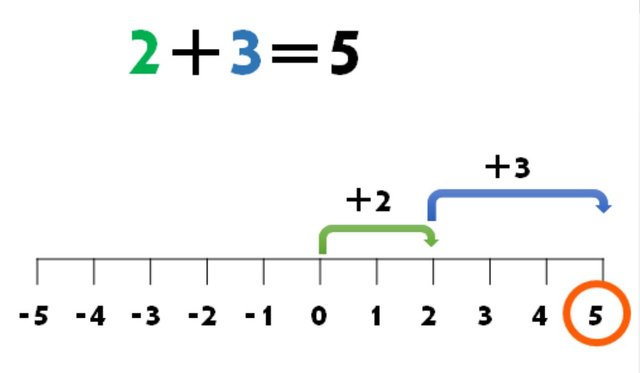
Iniciamos en la recta numérica en el cero (0), por ser el 2 un número positivo, vamos a avanzar en la recta numérica dos pasos a la derecha, hasta detenernos en el punto dos como lo indica la flecha de color verde. Luego continuamos en la misma dirección, esta vez dando tres pasos, hasta llegar al punto 5 de la recta numérica como se muestra en la flecha azul. Por lo tanto 2+3=5

Caso 2: Cuando ambos números son negativos
Signos IGUALES se SUMAN y se conserva el signo
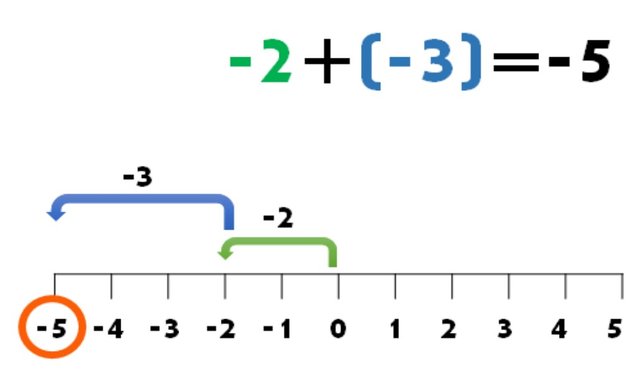
En este caso notamos que ambos números tienen el mismo signo, con la diferencia de que esta vez ambos son negativos. Por ello debemos avanzar hacia el lado izquierdo. Iniciamos en cero (0), avanzamos 2 pasos al lado izquierdo y desde el punto en el que quedamos vamos a avanzar 3 pasos más en el mismo sentido. Hasta llegar al punto -5 de la resta numérica.

Caso 3: Cuando se tiene un número positivo y otro negativo y el mayor valor absoluto de ellos lo tiene el número negativo.
Signos DISTINTOS se RESTAN y se coloca el signo del número con mayor valor absoluto.
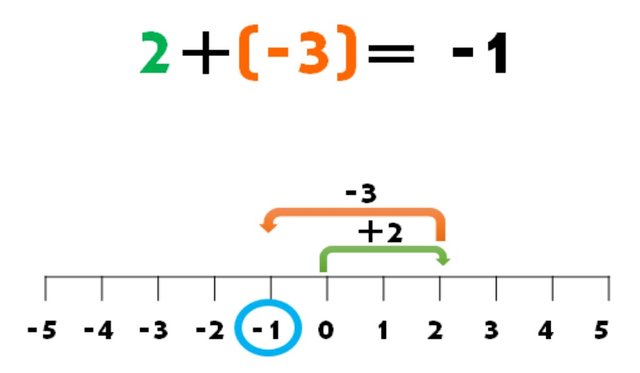
Es este caso podemos notar que el número 2 es positivo, por ello avanzamos al lado derecho, una vez allí, al igual que indica la flecha naranja, avanzamos al lado izquierdo porque -3 es negativo. Hasta detenernos en -1. Por tanto 2+ (-3)= -1

Caso 4: Cuando se tiene un número negativo y otro positivo y el mayor valor absoluto de ellos lo lleva el número Positivo.
Signos DISTINTOS se RESTAN y se coloca el signo del número con mayor valor absoluto.
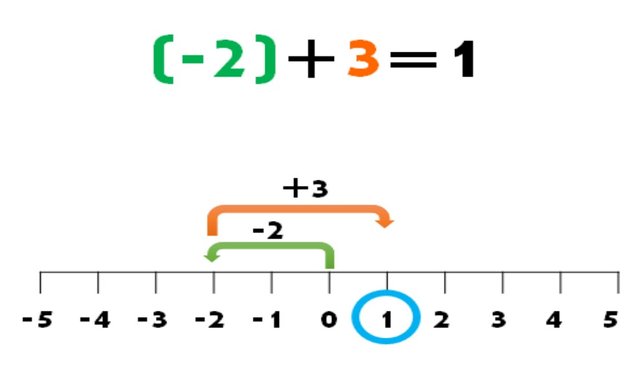
Es este caso podemos notar que el número 2 es negativo, por ello avanzamos al lado izquierdo como vemos en la flecha verde, luego al igual que indica la flecha naranja, avanzamos al lado derecho porque 3 es positivo. Hasta detenernos en 1. Por tanto (-2)+ 3= 1

En los ejemplos anteriores pudimos observar el porqué de la regla de los signos para la adición de enteros, simplemente podemos imaginar que la recta numérica es el suelo y que si el número es positivo damos pasos hacia adelante y si es negativo los pasos serán hacia atrás. Cuando los pasos van en la misma dirección, se van sumando y cuando tienen signos distintos es como ir hacia atrás y hacia adelante, por lo cual, restamos.
Tenemos entre otros ejemplos el caso del dinero, cuando el dinero entra a nuestras cuentas se va sumando, hasta tener un total de ingresos, y si por el contrario lo que hacemos es gastar y gastar, estas cuentas se van acumulando hasta tener un total de egresos. En ambos casos de SUMA porque las cuentas tendrían la misma naturaleza. Por otra parte si lo que tenemos son entradas y salidas de dinero, procedemos a restar para saber si aún nos queda dinero para gastar (saldo positivo) o si tenemos cuentas por pagar, en otras palabras deudas o saldo negativo.
Ejemplos:
4 + 3= 7
-4 + (-3) = -7
4 + (-3) = 1
-4 + 3 = -1
Podemos notar que en cada caso el resultado es distinto, esto se debe a que lo signos también lo son.

Ejercicios: Completar la siguiente tabla