PRELIMINARES
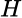será un espacio de Hilbert complejo y 
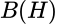el espacio de sus operadores acotados. Si para cada sucesión acotada 
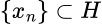, existe una subsucesión 
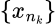y un vector 
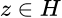, tales que 
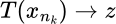, se dice que el operador 
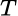es compacto.
Recordemos que si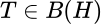 
, existe 
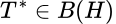tal que 
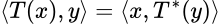, para todo 
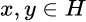. Al operador 
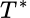se le llama el adjunto de 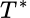. Si 
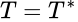se dice que el operador es autoadjunto y si 
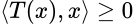para todo 
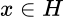que el operador es positivo. Es conocido que todo operador positivo es autoadjunto. Además si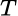
es un operador positivo, existe un único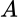 
operador positivo tal que 
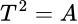. Es decir 
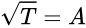. Dados los operadores 
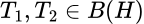, diremos que 
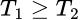si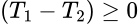 
. Un operador 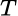es una isometría si 
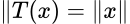para todo .
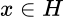Ejercicio 1:
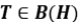, demuestre que 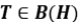es un operador compacto, si y sólo si, 
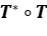es compacto.
Solución: Supongamos que 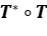es compacto y consideremos una sucesión acotada 
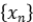en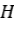 
, existe por lo tanto 
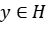, tal que 
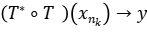en la topología de la norma. Tenemos que 
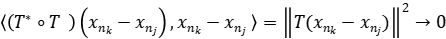, se deduce el recíproco y el directo es obvio.
Ejercicio 2:
Si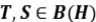 
, demuestre que si 
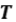es un operador compacto y 
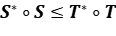, entonces 
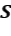es compacto.
Solución: Supongamos que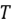 
es compacto y consideremos una sucesión acotada 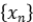en 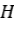, existe por lo tanto 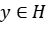, tal que 
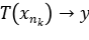en la topología de la norma. Sabemos que 
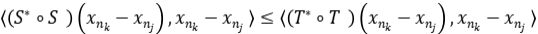, deducimos que 
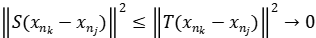y por lo tanto el resultado.
Ejercicio 3:
Si 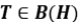es un operador acotado por abajo, entonces 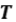no es compacto.
Solución: Si 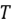es compacto y acotado por abajo, existe un número real 
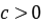, tal que 
⟹ 
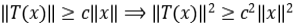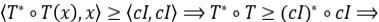
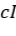es compacto, lo que es contradictorio.
Ejercicio 4:
Si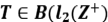 
es el operador definido por 
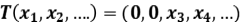, demostrar que es auto adjunto y positivo. Halle su raíz cuadrada.
Solución: Note que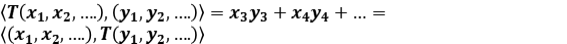 
.
Por otro lado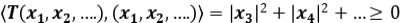 
.
Como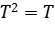 
, deducimos que 
.
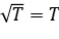Ejercicio 5:
Si 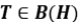es un operador acotado auto adjunto y positivo, pruebe que 
.
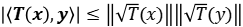Solución:
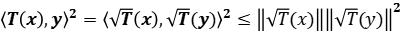, de lo que se deduce lo pedido.
Ejercicio 6:
Si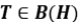
es un operador acotado auto adjunto y positivo, pruebe que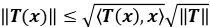 
. Deduzca de lo anterior que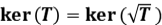 
Solución: Sabemos que por ser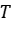 
un operador positivo, vale que 
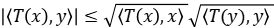. Sustituyendo en la fórmula anterior 
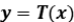, tenemos:
.
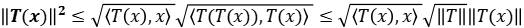Se deduce el resultado.
De la fórmula anterior deducimos que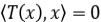 
, si y sólo si, 
.
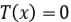Supongamos que 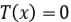, luego 
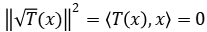y recíprocamente, es decir .
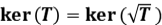Ejercicio 7:
Si 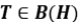es una isometría, pruebe que 
.
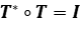Si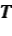 
es una isometría y 
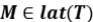, tal que 
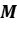reduce a 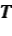, entonces 
.
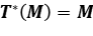Solución: (i) Sabemos que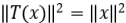 
, por lo tanto 
.
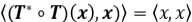Se deduce que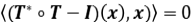 
. Como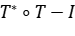 
es un operador positivo y auto adjunto, luego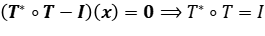 
.
(ii) Si 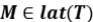, entonces 
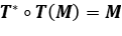. Por lo tanto 
.
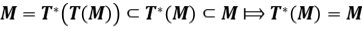Ejercicio 8:
Halle un operador 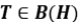que no sea auto adjunto y que sea idempotente.
Solución: Considere el operador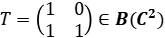 
, no es auto adjunto y es claro que .
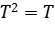FUENTE
Erwin Kreyszig (1978): Introductory Functional Analysis with Applications. John Willey & Sons. New York.