L'ago di Buffon

Pi greco ( π ) , la costante matematica più famosa di tutte, il rapporto tra la circonferenza di un cerchio e il suo diametro.
Pi greco è un numero irrazionale, ovvero non esprimibile come rapporto tra due numeri interi.
Le prime cifre le conoscimo tutti: 3,14. Ma dopo la virgola le cifre decimali continuano all'infinito. Ad oggi non è noto se ci sia uno schema nell'ordine delle sue cifre, se esse compaiano casualmente o meno.

Per determinare il valore di π esistono tantissimi procedimenti matematici, per così dire, "astratti", cioè metodi che richiedono di riempire il foglio di calcoli.
Possiamo calcolare quel numero in modo più divertente? Si, possiamo farlo sfruttando una matita (o un ago!) sottile e un foglio di carta.

(da wikipedia)

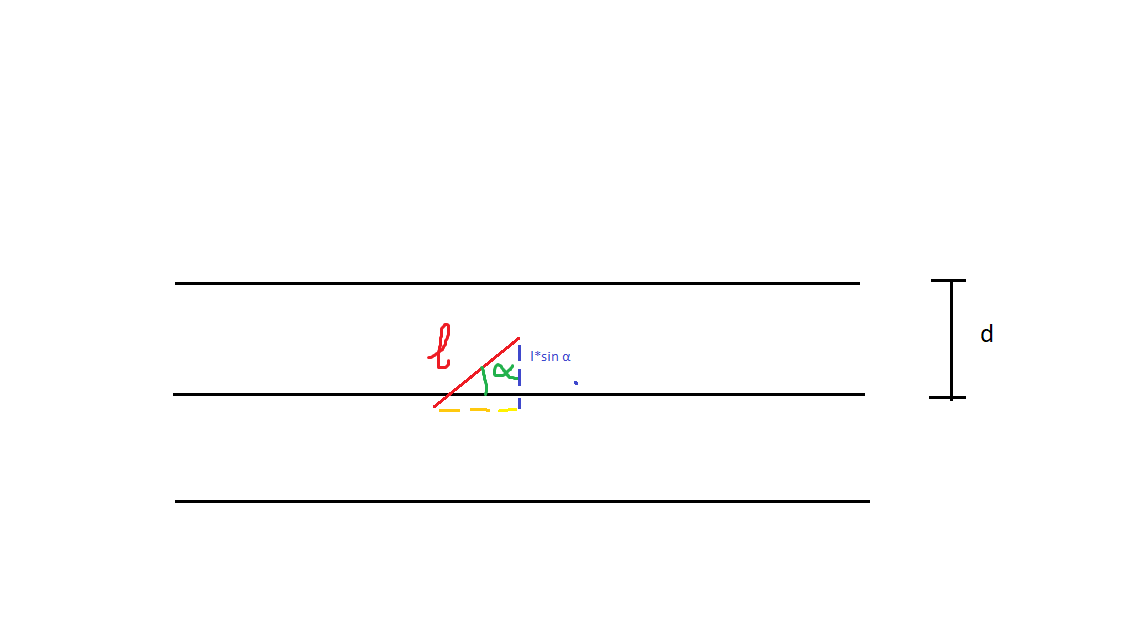
Parliamo dell' "Ago di Buffon", ovvero un quesito proposto da Georger Leclerc, conte di Buffon, nel diciottesimo secolo. La situazione che ci viene proposta è la seguente: immaginate di tracciare su un piano tante linee parallele, a distanza d. Qual è la probabilità che, lanciando casualmente un ago di lunghezza l (con l<d), questo intersechi una linea?

I calcoli successivi li inserisco per completezza, non importa se non capite l'integrale, da li in poi è tutto facile ;)

Dunque, lanciando un ago casualmente questo formerà un certo angolo con le linee, che chiamiamo alfa.
A noi interessa solo lo spazio occupato lungo la verticale, ossia ortogonalmente alle linee parallele. Infatti, è questa porzione di spazio l'unica che può intersecare le linee, e quindi l'unica che influisce sulla probabilità che stiamo cercando.
Per semplici regole trigonometriche, la porzione verticale sarà data da

Quindi la probabilità è una funzione data dal semplice rapporto tra lo spazio occupato verticalmente e lo spazio totale d

(2)

A questo punto dobbiamo fare ricorso al teorema della media integrale. Esso afferma che data una funzione continua f(x), a valori nell' intervallo [a,b], esiste un punto c appartenente ad [a,b] tale che

Adesso poniamoci nel nostro specifico caso.
La nostra funzione ha valori nell'intervallo [0, π ], dove π è l'angolo piatto (180°), che è appunto il valore massimo che l'ago può formare con le linee.
Qual è il senso dell'operazione che stiamo per fare?
La probabilità dipende da alfa, che a sua volta cambia a ogni lancio, perchè questo è casuale.
Usando l'integrale noi stiamo immaginando di calcolare la probabilità (espressa dalla formula 2) per ognuno degli infiniti angoli tra 0 e π, e di sommare tutte queste probabilità tra di loro.Se ora dividiamo questa somma per la grandezza dell'intervallo considerato otteniamo appunto il valore medio della funzione probabilità
NOTA: Valore medio non significa il valore che sta a metà tra il minimo e il massimo, ma il valore che mediamente la funzione assume nell'intervallo. Calcoli!

(3)
che è la probabilità media che un ago intersechi una linea.

Passiamo alla pratica.
Iniziamo lanciando l'ago. Una volta, due volte... n volte. Lanciando l'ago un numero infinito di volte abbiamo esattamente quello che ci serve: un numero infinito di angoli, che è la condizione necessaria per calcolare il valore medio della funzione.

Giriamo la formula 3 ed otteniamo che π è dato da

dove p è la probabilità.
Noi però dobbiamo misurare sperimentalmente questa probabilità.
Per definizione, la probabilità di un evento è data dal numero di casi favorevoli (S) diviso il numero di prove (P). Se per esempio effettuiamo 100 lanci, e 47 volte l'ago interseca una linea, allora la probabilità che calcoliamo è di

Inseriamo questa formula nella 3 ed otteniamo

ovvero la formula che si serve in pratica per effettuare l'esperimento!

Come già detto, più lanci effettuiamo, maggiore sarà l'approssimazione di pigreco, perchè maggiore è il numero di angoli che otteniamo, ovvero la nostra p tenderà ad assumere un valore che rende vera quell'uguaglianza.

Il matematico italiano Mario Lazzarini, nel 1901, fece l'esperimento lanciando circa 3400 volte l'ago. Ottenne un'approssimazione di pigreco precisa alla settima cifra decimale, un risultato davvero notevole.

La cosa bella di questo problema è che mostra come π sia insito anche dove tutto è governato dal caso. Una costante determinata da qualcosa che costante non lo è mai.
Potete fare la prova a casa! Contate i lanci e applicate la formula!

Fonti:
https://en.wikipedia.org/wiki/Buffon%27s_needle