CARACTERIZACIÓN HOMOLÓGICA DE MÓDULOS PLANOS

Recordemos que un módulo M sobre un anillo conmutativo con unidad A, es un A-módulo plano, si dada una sucesión exacta corta de R-módulos:

Entonces es exacta

Queremos dar una caracterización homológica de los módulos planos:

---

---

1. Sea 𝑨 un anillo conmutativo con identidad y 𝑴 un módulo sobre 𝑹. Son equivalentes :

(1) 𝑴 es plano

(2) Tor_n ^A (M,N)=0, ∀ N módulo sobre A.

(3) Tor₁ ^A (M,N)=0, ∀ N módulo sobre A.

---

---

(1) ⟹ (2) Sea una resolución proyectiva del módulo N:

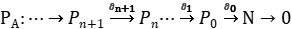
Como 𝑀 es plano es exacta

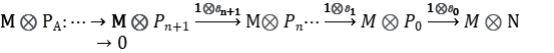
Por lo tanto los grupos de homologías H_n (M⊗P_A)= Tor_n ^A (M,N)=0 ∀ n > 0.

(2) ⟹ (1) Obvio.


(3) ⟹ (1) Consideremos una sucesión exacta

Para M consideremos la resolución proyectiva:

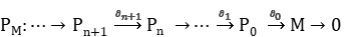
Como cada P_n es un módulo plano, son exactas las sucesiones

(*)

Podemos asociar a cada módulo resoluciones proyectivas:

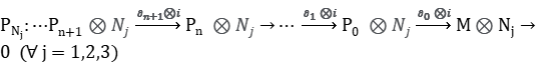
y morfismos de complejos

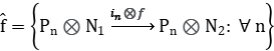
y

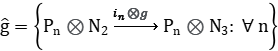
de tal manera que es exacta

Obtenemos la sucesión exacta

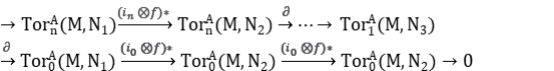
Es decir es exacta

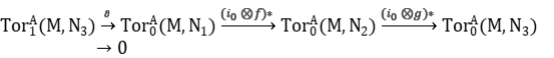
Se deduce que

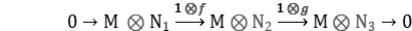
lo que termina la prueba.

---

---

2. Dada una sucesión exacta

tal que M₃ es un módulo plano. Veamos que M₁ es plano, si y sólo si, M₂ es plano.

---

---

Supongamos que M₁ es plano, De la sucesión exacta

y del ejercicio anterior, deducimos que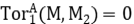

lo que prueba el directo.

Para ver el recíproco, considere

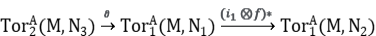
Se deduce que 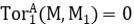lo que termina la prueba.

---

---

3. (a) Un módulo M es plano, si y sólo si , Tor₁ ^A (M,N)=0, ∀ N módulo cíclico sobre A.

(b) Un módulo M es plano, si y sólo si , Tor₁ ^A(M,A/α)=0 , ∀ α ideal de A finitamente generado.

---

---

(a) Recordemos que N es un módulo cíclico, si es generado por un solo elemento. Supongamos que N es un módulo finitamente generado, luego N=Rm₁ +....+Rm_n con m_j∈M. Considere los submódulos N_j=Rm₁ +....+Rm_j. Es claro que N₁⊂...⊂N_n=N y cada módulo cociente N_j/ N_j−1 es cíclico. Supongamos que valen las hipótesis del recíproco; entonces Tor₁ ^A (M,N_j/ N_j−1)=0. Sabemos que es exacta:

Consideremos

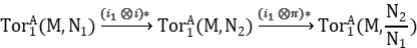
y como

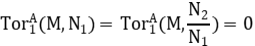
se deduce que

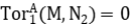
Procediendo de esta manera se demuestra el recíproco. El directo es obvio.


(b) Un resultado conocido es que, M es un módulo plano, si y sólo si, para cada ideal finitamente generado α de A, es exacta

Sea la sucesión exacta

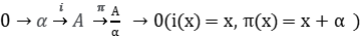
De la expresión

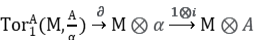
De lo que se deduce

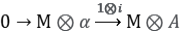
lo que prueba el resultado.

Nota. Es importante señalar que los tres resultados presentados son soluciones a tres ejercicios que sobre módulos planos y homología presenta el libro "Introducción al Álgebra Conmutativa " de Atiyah-Macdonald (Editorial Reverté, 1978)