How to make Mental Arithmetic Easier – N i ne Tricks

Even children or adults, people who calculate quickly are purely cool. There are times when mental calculation is much earlier than unlocking the smartphone and waiting for the start of the calculator application.

Here are the is a 9 tricks to make mental arithmetics easier to introduce. To be honest, it is somewhat confusing, but if you find a way to match yourself, you may be able to memorize mentalize it from two or three digits to billions

1. From left to right (add / subtract)

Example: 58 + 26 =?

First of all, please try to solve it as usual.

It is a general desk calculation method to add or subtract two or more digits from right to left, that is, from the first digit .

So how about calculating this from left to right, that is, from the second digit ?

1) 50 + 20 = 70
2) 8 + 6 = 14
3) 70 + 14 = 84

(1) First calculate the digit of the tens digit, (2) then add the digits of the first place. (3) Finally putting them together ... the way to say. If it was easier to calculate the method learned at elementary school on a desk, it is one thing to try the exact opposite approach in mental arithmetic.

2. Simple Small Numbers

Example: 593 + 680 =?

Well this time it's 3 digits of addition. A fine number 593 seems to be slightly troublesome, but let's replace this with a number that is easy to calculate as follows.

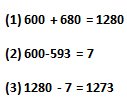
(1) First of all, calculate it by replacing the number 593 with a simple 600 number. (2) Of course, as it is it will increase by seven additions up to the answer, so (3) Let's subtract the amount increased last.

What do you think. Instead of trying to solve a calculation formula as it is, first replace it with a number that is easy to calculate, and finally fill that difference.

So the next in the same way multiplication what if solving?

Example: 89 × 6 =?

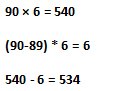
If you get used to it (first it is the first barrier to get used to), the mental arithmetic of 2 digits and 3 digits numbers seems to be pretty much alright.

3. Remember the Fraction and Decimal Rule

Do not neglect the numbers expressed by " percent ", " decimal ", and "fraction ". For example, if you remember "1 / n" such as 3/4 = 0.75, 1/6 = 0.166... ... it is not limited to business scenes dealing with quantitative data, but calculates a bargain sale from a bargain sale Until the scene to do, it might be useful on a daily basis.

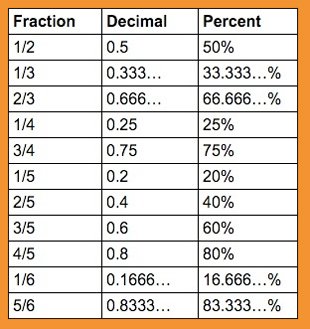
Here is the continuation of the table

4. Use the Numbers "0" and "5"

Here, "0" and the place at any time 1 multiplied by "10" 0, place of 1 multiplied by "5" 0 or 5 makes use of the law.

Example: 82 × 4 =?

To make the numbers simple again, let's consider how to split 82 into 80 and 2, multiply each by 4 and add them up.

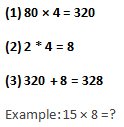
Example: 15 × 8 =?

Also, if the number is "15", multiply it by 10 first, add half the number (*) and reach the answer. That is, it is as follows.

10 × 8 = 80
5 × 8 = 40 (It is OK even * 80 ÷ 2 = 40)
80 + 40 = 120
Example: 16 × 24 =?

When applying the same method, multiplication of "16" can be easily solved.

In the case of 15, it was simply half, but in this case of 16 it increases by 15 from 1 (16-15), so it is the point that adds the number (24) divided by that number to the end. If there is no last addition (*), it will be a 15 × 24 answer so be careful.

10 × 24 = 240
240 ÷ 2 = 120
240 + 120 + 24 (*) = 384

5. Mastering multiples

Let's memorize multiples of the squared numbers from 1 to 20, really help in mental arithmetic ... First of all, let's try the following example (assuming that you can not mental arithmetically) for clarity.

Example: 10 × 4 =?

First of all, if we take the numbers between 10 and 4, it will be 7.

(10 + 4) / 2 = 7

The difference between 7 and 7, which is the average of 10 and 4, is 3.

10-3 = 7
4 + 3 = 7

I will use multiples here. A multiple of 7 is a multiple of 49, 3 is 9.

49-9 = 40
So, it was 10 × 4 = 40.

Let's increase the difficulty level and let's solve the next example in the same way.

Example: 15 × 11 =?

(15 + 11) / 2 = 13
15-13 = 2
13 - 11 = 2

The multiple of 2 is 4, the multiple of 13 is 169

169 - 4 = 165

was.

6. Give Rough Figures

It is Fermi estimation that is useful when thinking about the number of "about" like tens of millions, millions, hundreds of thousands ... and so on .

7. "Reflag" and "Rearrange" the Numbers

Example: 5 × (14 + 43) =?

The expression became somewhat complicated, but how to face it is almost the same as before.

First of all, paraphrase 43 to 40 in an easy to understand manner.

Then calculate the remaining 3 (43 - 40) together. That is, it is as follows.

(5 x 14) + (5 x 40) + (5 x 3) = 285

When rearranging complex expressions like this, do not forget to follow the order of calculation.

8. It is OK, If the Answers Match 

Example: 5 × 28 =?
(1) 10 * 28 = 280
(2) 280/2 = 140

It looks like the number 10 suddenly came out, but what you are doing is simple. (1) Multiply 5 by 2 (2) How to divide answer that came out by 2.

Example: 24 × 4 =?
24 × 2 × 2 = 96

In this example, we calculate 4 = 2 × 2. In the same way of thinking, the little big numbers even in small numbers factorization will be easier to solve Then all at once.

9. There are calculation methods for numbers above 100 million units

Example: 44 billion ÷ 400,000 =?

(1) First of all, to calculate how much the answer will be hundreds of thousands, millions, calculate the number of "0". There are 44 billion in 44 million, and there are 9 "0" , while 400,000 is 400,000 and 5 is "0".

(2) Next, divide the number ("44" and "4" in the example) of the part which is not "0". (3) Finish the calculation using the numbers given in (1) and (2) at the end.

1) 10 9 ÷ 10 (5th power)
2) 44 ÷ 4 = 11
3) 11 × 10 (9th power to 5th power)
= 11 × 10 (4)
= 110,000

If you can choose from various scenes and what numbers you calculate, you will feel that everyday life will change a bit without your smartphone .

---