I have been writing the post related with gamma function, but among them I didn't show the equivalence between various version of gamma function. So in these series of posts we will prove the its equivalence explicitly.
Followings are my previous posts on computation with gamma function
[math, computation] Euler-reflection formula-version 1 : Basel Problem
[math, computation] Euler-reflection formula-version 2 : complex integration
[math, computation] Euler-reflection formula-version 3 : Differential equation
[math, computation] The expansion of gamma function 1 - Basic
[math, computation] The expansion of gamma function 2 : Derivation and application

As a first part, in this post, we will see the definition of facotrial, Gauss and Euler's version are equivalent.
Gauss
The defitinio of Gamma function by Gauss
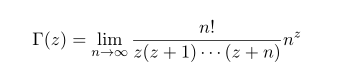
In this form of Gamma function, we have factorial and exponential function. This definition usually used for derivation of striling forumla
Let's see that this Gauss's definition is actually (z-1)!
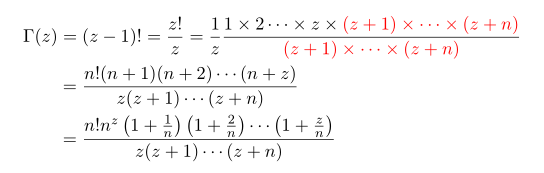
Note since n here is arbitrary number, we can particulary pick n as infinity. Thus by limit_{n->infinity} (1+k/n)=1 we have
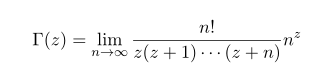
Thus indeed we have shown that the definition of gauss function are factorial
Euler
The Euler's version of Gamma function
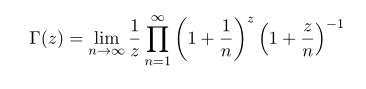
This expression is written in terms of products of infinite terms.
Here we will show that this definition is equivlaent to Gauss's version. Since in the above we shoe that Gauss's version is equivalent to Factorail this shows that Gauss=Euler=Facotrial.
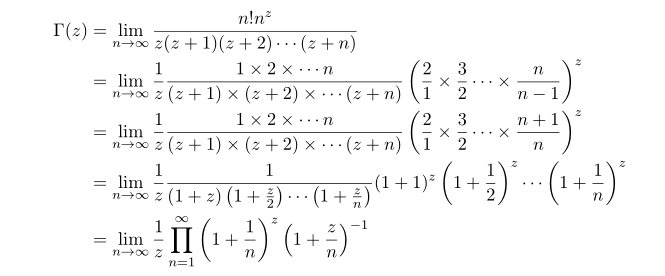
In the middel we used
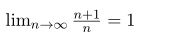
and
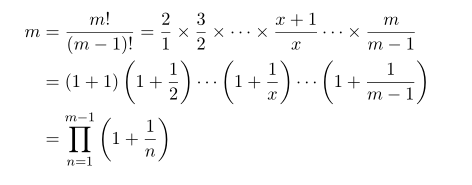
보기만 했던 감마함수가 이런 식으로 나오는 거였군요ㅎㅎ 과정은 처음 보네요... 역시 어렵습니다ㅠㅠ
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit