This is a English version of my former post in korean .
In My previous posting about Riemann hypothesis, [which was written in korean] I state reflection formula of zeta function to obtain non-trivial zeros
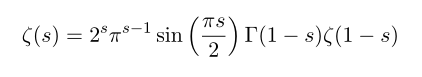
In the derivation of this formula one needs Euler-reflection formula
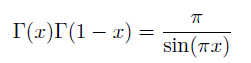
The most famous proof of this is using expression of gamma function and sin function as a infinite products. As i talk in the previous post about Riemann hypothesis in korean, there are three ways [of course there are more!!] of showing this.
- 1 . Basel Problem
- 2 . Complex integration
- 3 . Differential equation
In this post firstly, i will talk about the most popular proof which starts from the re-definition of gamma function and sine function.
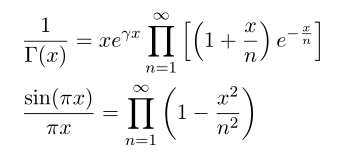
First equation for gamma is nothing but the alternative definition of gamma function, and for the second expression of sine function it is nothing but Euler's approach of Basel problem. I attach my notes for this expression

Now come back to our Euler-reflection formula. You can see it is nothing but just plugging the functions and compute properly. [So it is most popular and easy proof in some sense]
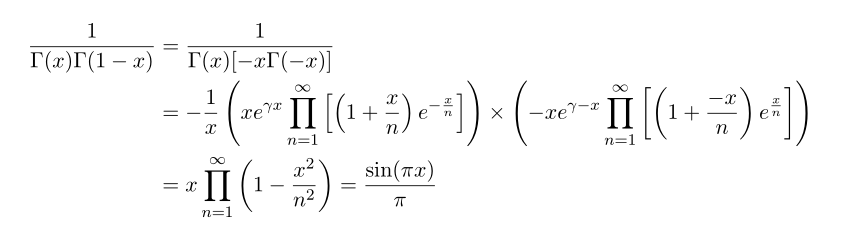
Now we are done!