I frequently enjoy computation or derivation of proper integral and properties of special functions, today i want to talk about Riemann zeta function. First, it is defined as sum of series like
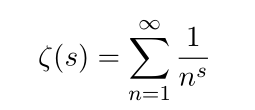
Noticing that condition Re(s)>1 is very important!, for these value the Riemann zeta function has convergent value.
Especially for s=1 we have
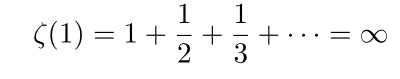
divergence!. This is known as Harmoic series. And from p-test we can see for s>1 this series sum converges. Interesting points is for s=0 or s=-1, by introducing uv-regulator we have finite convergence
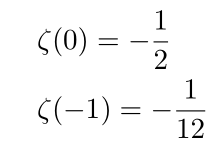
the relavant computation might be covered in the near future. The purpose of today's post is computation of even s. It is well known that for even s, we have exact convergence.
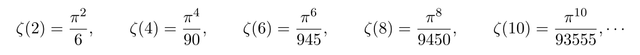
There are many ways to obtain these results. Famous way is using the techniques in complex analysis, Fourier transformation, Parseval's theorem etc.
If you are interested in particular values of Riemann zeta function see this post
https://en.wikipedia.org/wiki/Particular_values_of_the_Riemann_zeta_function
What i want to introduce today is not that fancy method. Only knowledgement at the level of freshman calculus course we can evalualte the value of zeta function for even s.
To do that first you know taylor expansion. Taylor expansion is a series expansion of a function at a given point (here let that point be "a")
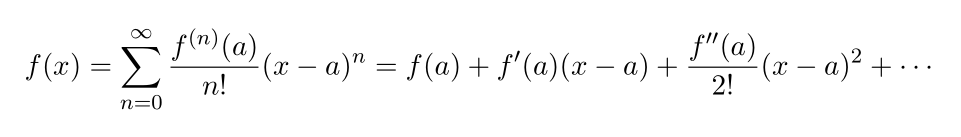
the upper script denotes derivatives n times. with this taylor series we can prove
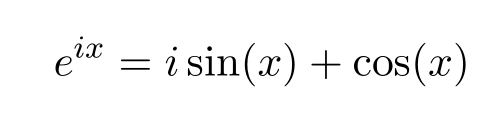
after plugging x=\pi/2 and reordering we have Euler's identity.
To our computation we need taylor series for log, for |x|<1, we can expand
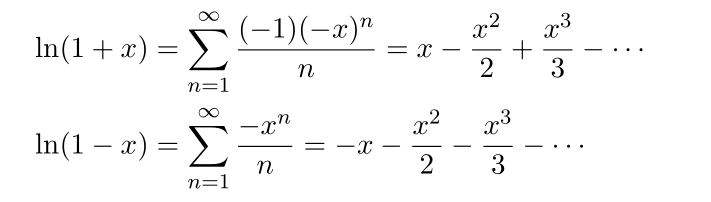
substracting
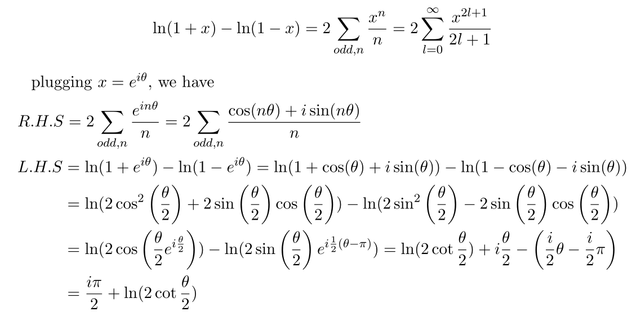
comparing two sides we have
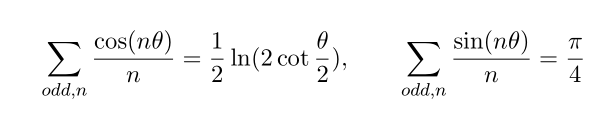
Now integrate the second equation with repsect to theta, along 0 to theta we have
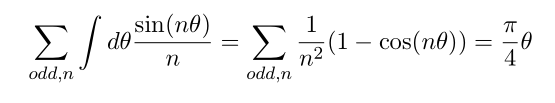
plugging theta=\pi/2 we have

From this equation we can compute zeta(2)
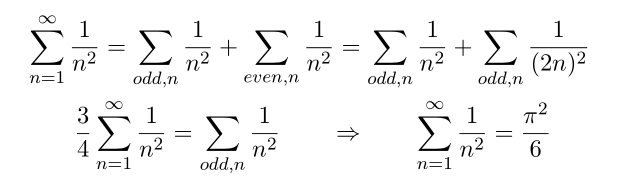
From previous results,
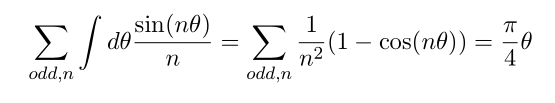
plugging corresponding results for pi^2/8 we have
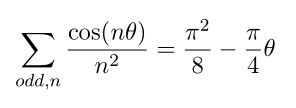
Now by repeatting same procedure we can compute zeta(4)
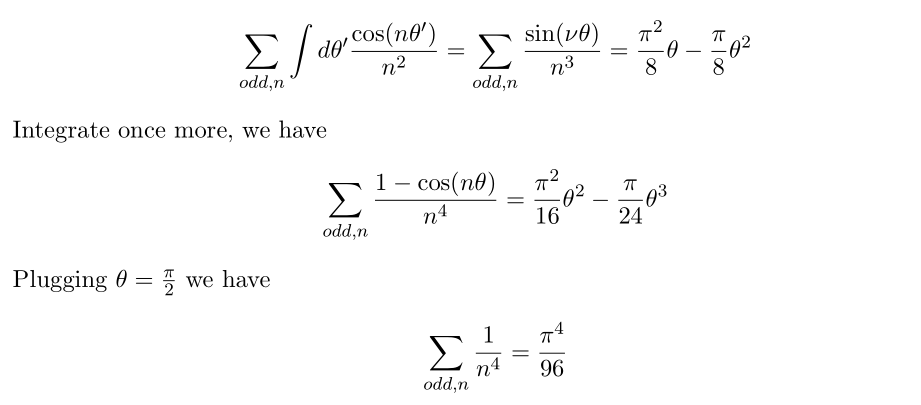
from similar way which we used before we have
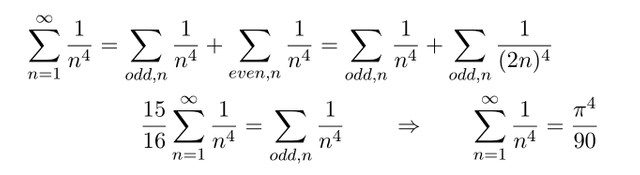
Now to go further, we can obtain zeta(6), plugging theta = pi/2 to our previous equation
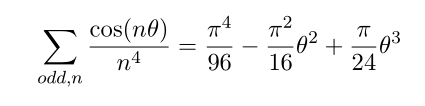
integrate this and reodering for 1/n^6, we can do the same thing.
In this way we can compute all even s for zeta function exactly. Of course one can do the other method or just using mathematica.
I hate Math haha
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This comment has received a 0.15 % upvote from @booster thanks to: @hamzaoui.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Oh no that's too sad.....
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
haha yeah
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This comment has received a 0.15 % upvote from @booster thanks to: @hamzaoui.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit