In this series what i want to derive is following equation
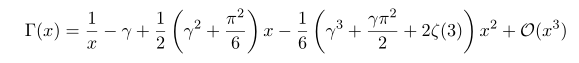
This fomrula frequently appear in physics and enginerring, but the derivation process does not well described. Using mathematica one can expand more hihger order terms without hesitiate. But here what we are going to do is derivation of this equation by hand. To do that, first in this post i will try to describe some basics in detail
The many definitions of gamma function
The most popular definition of gamma function comes from factorial. Using integration by parts for integer z we obtain factorials of z-1.
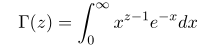
Euler's version of gamma function
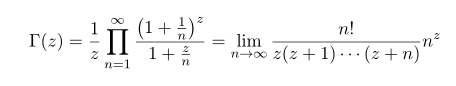
Weierstrass's version of gamma function
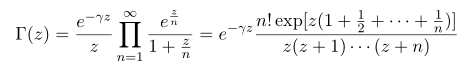
Note that in this defintion, the constant gamma is defined as
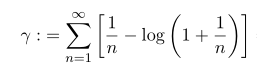
The differential forms of gamma function
When you dealing with gamma function, you frequently encouter its derivatives and higer deriviatives. like digamma, trigamma, polygamma etc.
First diagamma function is defined by
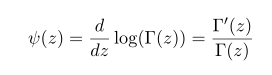
Interesting facts is due to recursive properties of gamma function, these polygamma also have some recursvie properties.
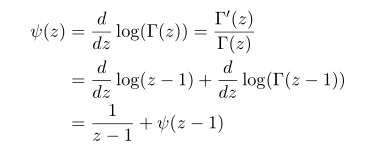
Solving this relation we have
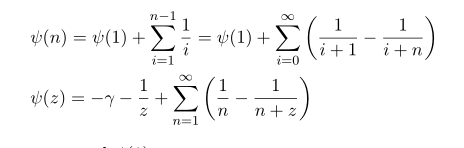
In the process we used which we will prove this later.
which we will prove this later.
Now differentiate psi with respect to z

again same way as before we have
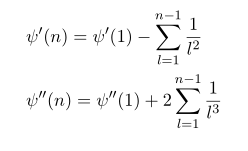
We can re-express these di, tri gamma functions into gamma function as follows
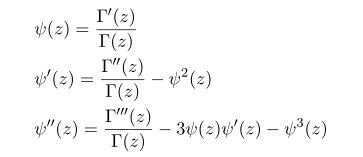
Basically these are obtain from the direct differentiation of first line.
The value of psi(1), psi'(1), psi''(1)
Since we didn't set initial values, to solve them exactly we need to figure out its initial values.
Starting from the definition of Euler's version of gamma function by taking Logarithm and take differential we have
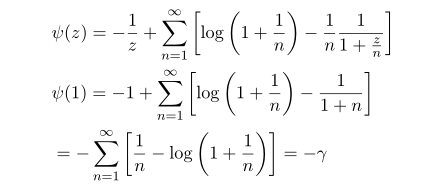
Plugging back to the form of digamma function we have
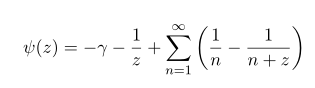
Since constant gamma vanishes upon on differentiation, by taking derivatives
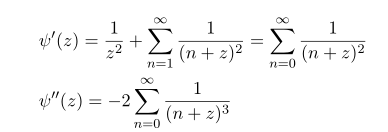
plugging z=1 we have

The computation related with zeta function you might refer my previous post on zeta function of even case
With these equations we can obtain
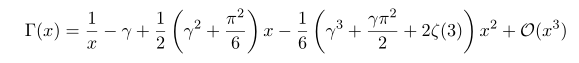
I will post relevant computation in upcoming post.
My post on gamma functions
[math, computation] Euler-reflection formula-version 1 : Basel Problem
[math, computation] Euler-reflection formula-version 2 : complex integration
[math, computation] Euler-reflection formula-version 3 : Differential equation