[math, computation] zeta 4 : version 1-trigonometric function

In this series of post, I'd like to mention how to compute zeta 4, I am thinking about 3 different ways for showing this. Of course there are many more ways of showing this. Among many I pick up three some easy method, not knowing many advanced mathematical stuffs.

In my previous post I already talk about some method of computing even zeta function. (see my previous post [math, computation] Some easy trick for computing Riemann zeta functions of even numbers)

For this series I'd like to talk about some other method for computing this zeta 4.

As a first trial, using trigonometric function one can compute zeta 4 easily.

To do so, we need some notes in [math, computation] Euler-reflection formula-version 1 : Basel Problem

equipped with these equations and using expression of taylor series, we will going to compute zeta 4. First write down the taylor expression for sin and sinh

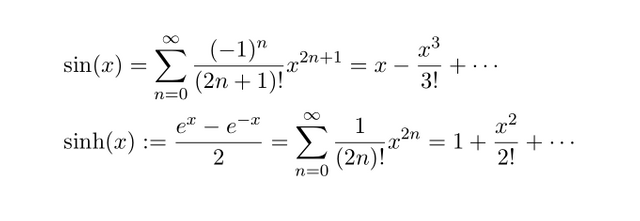
From this

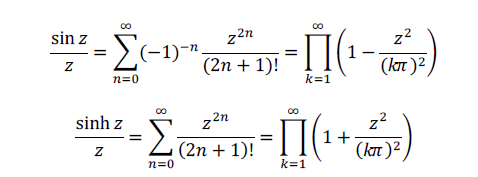
Multiply this and expand

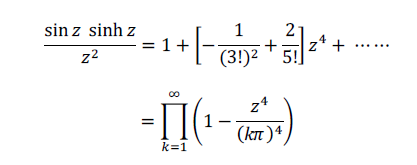
Collecting z^4 terms

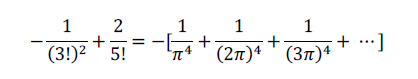
Now multiplying pi^4 then

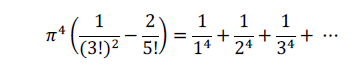
rewrite infinite sum into zeta 4 we have

By knowing some series expansion and products form of trigonometric function you can easily obtain some zeta functions, by properly manipulating orders of z.