[math, computation] zeta 4 : version 3 Parseval's theorem

In my previous posts

[[math, computation] zeta 4 : version 1-trigonometric function]
[[math, computation] zeta 4 version 2 -Fourier expansion]

We are talking about evaluating zeta 4 in two ways.

Using Parseval's theorem, we can even more easily compute zeta 4. First Parseval's theorem is related with Fourier expansion

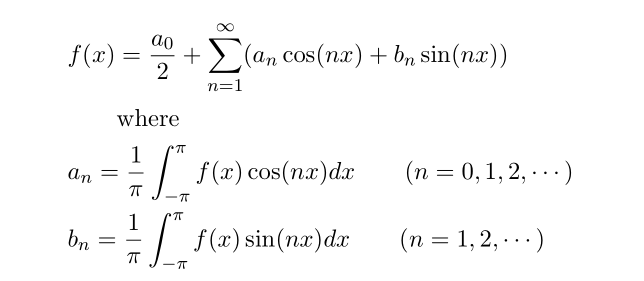
There are many types of Parseval's theorem, here we will use the expectation value of squares of f(x), which is related with Fourier coefficients.

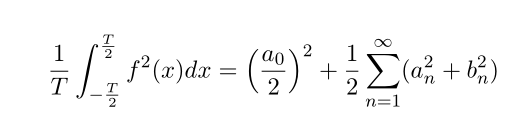
Using specific period and function f(x)

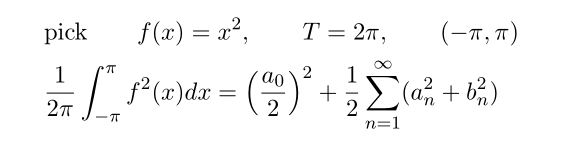
since f(x)=x^2 which is even function, b_n=0 thus we only compute a_n

From previous post on [zeta 4 with Fourier expansion]

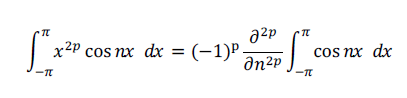
using above equation we can compute a_0 and a_n as follows

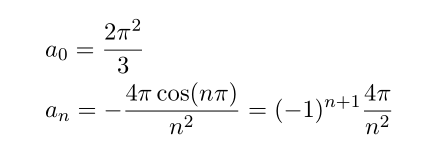
plugging this we have

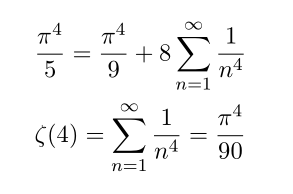
I guess this is the reason why many mathematicians are exciting about lemma and theorems! They are so powerful!