Hello steemians! It's finally pi day for those of you living in the Western Hemisphere. What's your favorite kind of pie? Feel free to weigh in after reading the post below.

If you haven't already seen my post about the connection between pi and quantum physics, feel free to check it out here.
The Euler Identity
The number pi has a number of interesting properties, probably the most famous of which was shown by Euler around 1750. The formula combines two other "interesting" numbers from mathematics, namely e (approximately equal to 2.71828), and i (defined to be the square root of -1) to form one of the most elegant identities known in mathematics.
Stated succinctly, the Euler identity is:
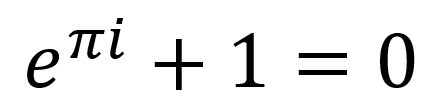
This may seem like a bit of mathematical witchcraft, but this is in fact a basic fact of a branch of mathematics known as complex analysis. Euler earlier discovered that:
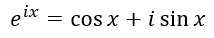
There are several proofs for this equation, but the most accessible probably involves using the MacLaurin series. And since this mainly intended to be about pi, we'll forgo this proof.
Anyhow, evaluating Euler's formula for x = π, we obtain cos(π) + i sin(π) = -1 + 0 = -1. Which, when added to 1, of course gives zero.
The beauty - and some might say irony - lies in the fact that both e and pi are irrational and transcendental numbers, and that i isn't really a physical quantity. Yet, when combined in this elegant manner, everything comes out to zero.
Also, it's worth mentioning that two famous people were born in March 14th: Wacław Sierpiński (1882), perhaps best known for the triangle that bears his name, and Albert Einstein (1879).