Se han identificado los parámetros específicos necesarios para gestionar un sistema propenso a conflictos. Al controlar dichos parámetros, se pueden crear condiciones para prevenir conflictos sociales
Un equipo de investigadores dirigido por el Profesor Asociado Alexander Petukhov del Instituto de Relaciones Internacionales e Historia Mundial de la Universidad Lobachevsky está desarrollando modelos de conflicto social sobre la base de dinámicas no lineales.
Para el modelado matemático, una característica importante de los procesos sociales y políticos es que no se pueden definir estrictamente. Siempre están sujetos a pequeños cambios y fluctuaciones. Muy a menudo, los procesos sociales se comparan con partículas brownianas. Estos pequeños cambios (fluctuaciones) en su trayectoria se explican por el movimiento caótico de otras moléculas. En los procesos sociales, las fluctuaciones pueden considerarse como manifestaciones del libre albedrío de los participantes individuales, así como de otras manifestaciones aleatorias del entorno externo.
En física, estos procesos generalmente se describen mediante la ecuación de difusión estocástica de Langevin, que también se ha aplicado para modelar ciertos procesos sociales.
El enfoque basado en tales ecuaciones tiene varias ventajas:
- Como ya se mencionó, permite tener en cuenta las manifestaciones del libre albedrío de los participantes individuales, así como otras manifestaciones aleatorias del entorno externo al sistema social.
El comportamiento del sistema social se puede calcular tanto para el conjunto como para sus elementos individuales.
Con este enfoque, es posible identificar algunos modos estables característicos del funcionamiento de los sistemas sociales, dependiendo de las diferentes condiciones iniciales.
Las ecuaciones de difusión como herramientas matemáticas están suficientemente validadas para ser utilizadas en la simulación numérica.
El modelo se basa en la idea de que los individuos interactúan en la sociedad a través de un campo de comunicación - h. Este campo, creado por cada individuo en la sociedad, modela la interacción de información entre individuos.
Sin embargo, debe entenderse que estamos hablando aquí de una sociedad que difícilmente es atribuible como un objeto en la topología espacial física clásica.
Según el Dr. Petukhov, desde el punto de vista de la transferencia de información entre individuos, el espacio en la sociedad combina coordenadas espaciales clásicas y características específicas adicionales. Esto se explica por el hecho de que en el mundo de la información moderna no hay necesidad de estar cerca del objeto de influencia para transmitir información a este objeto.
"Por lo tanto, la sociedad es un espacio multidimensional, social y físico que refleja la capacidad de un individuo para" llegar "a otro individuo con su campo de comunicación, es decir, para influir en ese individuo, sus parámetros y la capacidad de moverse en un espacio determinado". toma nota de Alexander Petukhov.
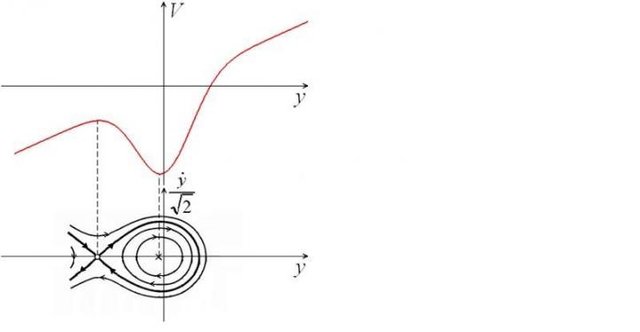
En consecuencia, la posición del individuo en relación con otras personas en dicho espacio proporciona un modelo del nivel de la relación entre ellos y de su participación en el intercambio de información. Cuando los individuos se encuentran cerca el uno del otro en este modelo, significa que hay un intercambio regular de información entre ellos, y se ha establecido una conexión social. En este contexto, la variante de interacción entre individuos o grupos de individuos resulta en un aumento dramático en la distancia (es decir, la distancia social? X = xi - xj, donde x es la coordenada en el espacio social y físico, i, j = [1, N], donde N es el número de individuos o grupos consolidados de individuos) entre ellos debe considerarse un conflicto.
Por lo tanto, suponiendo que un individuo es similar a una partícula browniana con cierto radio de influencia en otros individuos, el campo de comunicación puede representarse utilizando la ecuación de difusión.
Con base en el enfoque presentado anteriormente y el modelo desarrollado por los investigadores de la Universidad Lobachevsky, se revelaron los siguientes patrones característicos y las dependencias en las condiciones iniciales y de contorno:
- Se establecieron condiciones de frontera específicas, con la cuenta de influencia y control externo, bajo las cuales se crean los motivos para el surgimiento del conflicto social y su agravamiento. Tales condiciones están determinadas por los parámetros del sistema social.
Se encontró una región característica de estabilidad para un sistema social. En esta región, que está determinada por las trayectorias de fase, se mantiene una distancia social relativamente pequeña entre los objetos en estudio. Esta situación es característica de los grupos de población que interactúan activamente y están en contacto continuo con la información. Al mismo tiempo, se observó cómo cambia esta región, dependiendo de la influencia de la función de gestión del conflicto.
Al determinar y correlacionar estos estados límites con la parametrización introducida de la función de control, es posible determinar los patrones correspondientes a ciertos conflictos etno-sociales modernos. Por lo tanto, este modelo se puede utilizar como una herramienta para predecir dinámicas de conflicto y para producir escenarios de solución de conflictos.
"Al desarrollar este enfoque en el futuro, podremos crear sobre su base una herramienta para la previsión adecuada de los conflictos sociales", resume Alexander Petukhov.
Posted from my blog with SteemPress : https://matematicapositiva.com.ve/cientificos-de-la-universidad-lobachevsky-desarrollaron-un-modelo-matematico-de-un-conflicto-social/
I understand nothing, but let’s save math on steemit XD
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Well done @joseromerogc! You successfully guessed the match result.
Click on the badge to view your Board of Honor.
Do you want to know your current ranking? Read this post
Do not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - Round of 16 - Day 3
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit