I have to admit that I am stumped. It has been a while since I took graph theory. Here's the problem:
"Prove: If a graph has e edges and v vertices, and e > or equal to v, then the graph must contain a cycle. Note that it does not matter if the graph is connected or not."
In fact, I like this problem so much and want to know it, that I'll award the first person who can solve it 3 Steem Dollars as long as this post is still open. (I know 3 is not a lot but I'm just a broke mathematician philosopher).
Authors get paid when people like you upvote their post.
If you enjoyed what you read here, create your account today and start earning FREE STEEM!
If you enjoyed what you read here, create your account today and start earning FREE STEEM!
I think you can use induction to the number of vertices. Let G be a graph with only 1 vertex. To satisfy the condition "e is not less than v", it must have a loop. So, G has a cycle.
Now suppose that the statement is true for all graphs with number of vertices at most k. Consider a graph G with (k+1) vertices and suppose that |E(G)| is not less than |V(G)|. If G has no cycles, than it must have a "leaf", v_0. (A leaf means a vertex of a graph of degree 1.)
Now consider the graph H we get by removing the vertex v_0 from G. Then H is a graph with k=|V(G)|-1 vertices and |E(G)|-1 edges. So, the number of edges of H is not less than the number of vertices of H. By the induction hypothesis, H must contain a cycle. However, since H is a subgraph of an acyclic graph G, H cannot contain a cycle. This is a contradiction.
Now we see that the statement holds for all graphs with finite number of vertices.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
For the proof of the theorem that an acyclic graph with finite vertices must have a leaf, see the article "Acyclic graph must have a leaf" on math.stackexchange.com
There is a reply that shows a "tree(connected, acyclic graph)" with finite vertices has a leaf. One can easily generalize this theorem and prove that a "forest(acyclic graph)" with finite vertices must have a leaf.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Will do, thanks. I'm checking the proof right now. Thanks for the response.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I was just going over proofs on StackExchange and I think you're correct. I would be very impressed if you found this organically by yourself, but still since you answered it right I owe you 3 SD. I'll send that to you when I have that amount.

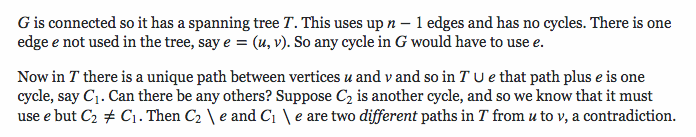

Here are some examples of the proof I found:
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit