Evaluating square roots some nice numbers that we talking about square root some numbers that you really want to remember are all the perfect squares
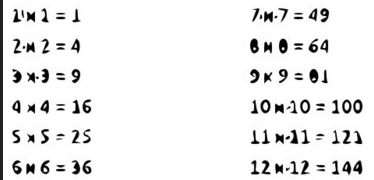
in other words 1 times 1 2 times 2, 3 times 3 all these results here 16, 25, 36... These numbers are all great numbers to look for and so memorize so that you can know that they are perfect squares and get the square root of some pretty easily
So if you want to memorize a list of a multiplication tables if you haven't already this is a really good list to start out with a little help you eventually one going through when factoring for square roots
So this lesson is a little bit about solving square roots that are not always perfect squares so it's pretty easy to solve them if they are, but if they not for example what if we are asked to solve the square root out 21

The first thing that we look for is it a perfect square or is there a factor that's a perfect square the factors of 21 are 1, 3, 7, 21 there's no perfect square factors so we'll go on to the next part that is estimated
What we would do with, 21 for example, is look at the two perfect square numbers that are around 21
So the square roots of 16 is 4 the square root of 25 is 5 so those are the two perfect squares they go on either side 21 that make sense 16 is the one that's to 21 and 25 is one that's just one greater than 21 alright and we look at and say, well 21 is right about between 16 and 25 so the square root of 21 is right about the middle between the square root of 16 and the square of 25 so that means it's approximately four-and-a-half (4.5)ok I will show some examples how to do this a little bit more
Here, let's look at another example first we use the calculator we find that the square of 21 is 4.58

This is just a way to check for accuracy all right, even more accurate than the abacus and alright looks practice a little bit if we're going to evaluate the square root of 27

the first thing that we do is find perfect square factors In this case 27 is 9 times 3,

9 is a perfect square so we can pull that out And find the square root of 9 is 3
 so in other words, this is 3 times the square root of 3
so in other words, this is 3 times the square root of 3
Now we have to find what is the value of the square root of 3 we're gonna look at perfect squares that are all-round the square root of 3 or around 3, 3 is between 1 and 4, 1 is a perfect square and 4 is a perfect square
So because 3 is between 1 and 4 the square root of 3 is between the square root 1 and the square root of 4 so between 1 and 2
It happened between 1 and 2 has 2 as square root of 4 so it's going to be about 1.6, 1.7 something like that
So if we wanna multiply that out and actually solve it's approximately equal to three times 1.7 or about 5.1

And with things like this this is a real estimate these on here, it's real if we use 1.6 would be a little bit farther off, but it wouldn't be that far off to be pretty close on wanna check with our calculator see that we're about the right area so that looks about, right.

But look at the next one the square root of 492

first thing that we do is we look for a perfect square factors have a perfect square factor of 4, 4 times 123 is 492

Will take the square root of 4 is equal to 2

And now what we need to do is find 2 perfect squares that are one that's just greater than one that just less than 123 from our original list we could take the square root of 121 at the square root of 144 so those are 2 perfect squares that are either side 123 one is lesser other greater than so because 123 is between 121 and 144 the square root of 123 is between the square root of 121 and 144 because it's really close to 121 yet its all estimating it closer to 121 or 144 well clearly it's really close to 121 just a little bit greater than that
The square root of 121 is 11 so we're going to say that it's about 11.1 or 11.2 okay cuz if 123 is really close to 121 the square root of 123 is going to be really close to the square root of 121 so a little bit biger
So we'll go ahead and say it's about 11.2 and we multiply them together 2 times 11.2 is 22.4 we can use the calculator find that it's actually 22.18

So we were pretty close 22.4, 22.1
You know it was. I mean it was pretty close if we'd used 11.12 it would have been a little bit closer, but you know, this is estimating when we estimate this is pretty close when we want something more accurate you definitely need to start checking with your calculator or doing other more advanced functions that will show you later on but for now estimating he just start using logic where does that fit 123 is between the 121 and 144 perfect squares still the square root is 123 is going to be between the square root of both of those numbers which one is a closer to and just give it a approximate decimal value