Problem solving strategies 

Image source

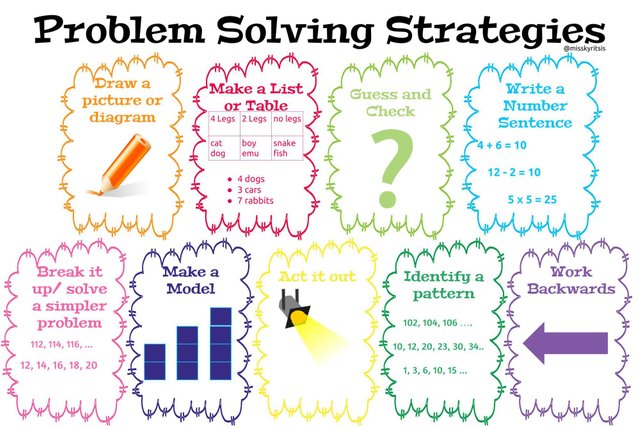
1. Look for a pattern
2. Make an organized list
3. Draw a table
4. Guess and check (Trial and improvement)
5. Work backwards
6. Use logical reasoning
7. Draw a diagram
8. Solve a simpler problem

After completing the first 2 problem solving strategies, we can look at the next two, drawing a table to organize data and the trial and improvement strategy.

3.  Make a table:

We can often solve problems involving relationships between 2 sets of numbers by drawing a table.  A table helps us to organize the data so that we can see the numerical relationship and to find the answer.

Example: 

In 2010, you bought a tree to plant in your backyard.  When you bought the tree, it was 1,2m tall.  Every year you measured the height of the tree and saw that it grows 0,2m every year. In 2010 you also bought another tree which was 0,2m tall and this tree grew 0,4 m every year.  In which year were these two trees the same height? 

Image source

NOTE:  Draw a table to organize the data about the heights of the plants.  

We can see that the height of the two trees were the same in 2015.

Activity:

A cellphone company check every 15 cellphones for software defects and every 20 cellphones for a hardware defect.  How often will a cellphone be checked for both the hardware and software defect at the same time?

4.  Guess and check (Trial and improvement):

Sometimes we are not sure on how to solve a problem in maths.  For this we have the trial and improvement strategy.  We guess!!  If it is wrong, we revise the first guess by adding or subtracting and we repeat this technique until we get the correct answer. 

Image source

Example:

At a fun fair, you use an equal number of $5, $2 and $1 coins to pay for a ride of $40.  How many coins did you use? 

Make a guess: 

Suppose you use 3 of each:

• The total will be 3 x $5 + 3 x $2 + 3 x $1 = $24 (too low)
• Revise:  Suppose you use 4 of each:  4 x $5 + 4 x $2 + 4 x $1 = $32  (still too low) 
• Revise:  Suppose you use 6 of each:  6 x $5 + 6 x $2 + 6 x $1 = $48 (too high)
• Revise:  Use the number between 4 and 6, which is 5 and try 5.5 x $5 + 5 x $2 + 5 x $1 = $ 40 which is the correct amount. 

You use 5 coins of each to pay for  the ride.  

Image source

Activity:

In a cricket match, Peter, the best batsmen in your team,  scored 50 runs before he was caught behind the wicket.  Peter scored an equal amount of 4s and 6s.  The rest of the runs was made by hitting nine 1s, four 2s and only one 3.  How many 4s and 6s did Peter score?  

Image source