
Every year, MIT hosts an "integration bee" in which first-year students compete to solve increasingly complex integrals using techniques they've learned in calculus. MIT's first integration bee was held in 1981, and has drawn large crowds ever since [1]. The competition usually consists of a qualifying round and a final round. Here is one of the questions from the qualifying round: (source)
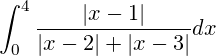
If you make it to the final round, you'll find that many of these integrals are far beyond the routine textbook exercises that most students will encounter, and require a bit of ingenuity, skill, and creativity to solve. The concepts needed aren't typically beyond those of a first year calculus course, but the idea is to find the "trick" behind them. Here is one such question from 2015 competition. Can you solve it?
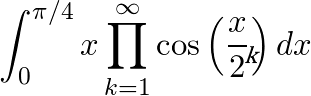
The entirety of the 2015 Integration Bee Final can be viewed here.
If you think you know, make a comment below. Don't cheat and watch the answer in the video!
Hint 1: Double angle formulas
Hint 2: L'Hopital's Rule
Just a quick note, the 2nd integral requires a k somewhere in the series term.
Sorry, gotta dash; back later!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You're right! I'm suprised I didn't notice it for an entire day. The correct integral is:
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
There is a full solution available online (for those interested) so I shan't repeat it - as it is also very long.
However, the key insight to solve that seemingly monstrous product is to use one of the trig identities - but in an unusual way - so that within just 2 or 3 terms the mind can see that the infinite product simplifies to just two terms.
Such problems are very much borderline A Level Further Mathematics - scanning the MIT paper, I think at least half of the problems could be done at school. Nowadays, a student would have to be studying Cambrdge's new Pre-U Level Mathematics as they have brought back all the topics that they have slowly removed from the (dumbed down) A Level.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I think that that's sort of the appeal of these sorts of problems. In and of themselves, they're not particularly difficult, but they require you to think outside of the box in order to get the solution. Once you see that light-bulb, the solution is obvious and elegant.
On your second point, yes, most of the problems could be done at school back in the day. I don't know the state of British mathematics education, but American maths education is in a sorry state. Most people can't wrap their head around the fact that 1/3 is in fact larger than 1/4.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Oh, I think we're in the realm of 1 in 10,000 who won't freak out just looking at that integral! There is a small counter-current holding on to mathematics as a rigorous subject; I mean, philosophy, for example, has almost totally disappeared from schools. Thankfully the maths competitions and Olympiads are away from the dead hand of government/corporate "mastery (obedience) learning". I teach a few gifted kids who haven't had their lights dimmed as yet, so that's fun!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I see that cos(x/2^1) = cos(2*x/2^2) = 1 - 2sin^2(x/2^2).
When k = 1, the product is cos(x/2^1).
When k = 2, the product is (1 - 2sin^2(x/2^2))*cos(x/2^2).
When k = 3, the product is (1 - 4sin^2(x/2^3)cos^2(x/2^3))*(1 - sin^2(x/2^3)*cos(x/2^3).
Does this lead to finding any useful pattern?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
The key step is using
sin(2x) = 2.sinx.cosx
so that
cos(x) = sin(2x)/2sin(x)
and by extension
cos(nx) = sin(2nx)/2sin(nx)
when plugged into the integral product, all the sines cancel out apart from the first and last terms.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Beautiful
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
DON'T CLICK ON HIS LINK, ITS A SCAM!! WATCH OUT FOR THIS PERSON!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
which one?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
the link that mr dimitrov10 wrote. I flagged him so his comment is not visible
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Ah now I see. Seems like my Smartphone Browser didn't even show that a comment is hidden.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
must be a smart anti-scam browser you got ;)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit