Hello my friends it's a me Drifter Programming again! Today we will talk about how we get the inverse of an square matrix, determinants and how we solve a linear system using determinants. So, if you have already checked out the Gauss method, then we can get started!
Inverse Matrix:
When talking about square matrixes we mostly also talked about the invertibility (if the matrix is invertible). If a matrix is invertible and represents a linear system then this system has 1 unique solution. So, when A*x = b is an linear system then x = A^-1*b, where A^-1 is the inverse of A. The inverse of a matrix is unique and thats why we have only one solution if the matrix is invertible.
Gauss-Jordan Method:
To invert a matrix we use the Gauss-Jordan method. When the canonical form of A is an identity matrix (diagonal matrix with '1's only) then A is invertible. So, to get the inverse we create an augmented matrix that contains A and I (A\I) and starting doing elementary operations until A becomes an identity matrix (I). After that where the identity matrix (I) was at the beginning now we have a new matrix that is the inverse of A (A^-1). If it's impossible to get an identity matrix out of A, then A is not invertible. Here is a good example.
Determinants:
The determinant of a square matrix is a real number that is represented by detA. This number is unique for each matrix and we can calculate only determinants of square matrixes! The determinant of an 1x1 matrix is equal to the value of the matrix (det[a] = a). To calculate the determinant of other square matrixes we have to use a specific formula that is called the Laplace extension, but I use another way that I find simpler. We also have easier ways for calculating the determinant of an 2x2 and 3x3 matrix that we will check in a sec. Another interesting determinant is that of an diagonal matrix, cause the determinant of such an matrix is simply the product of the diagonal elements. So, the identity matrixes have a determinant of 1 (det I = 1).
Determinant Calculation Trick:
Because, the determinant works with a recursion there is some kind of pattern occuring all the time. A determinant for a nxn matrix will contain the determinants of (n-1)x(n-1) matrixes and so on... This matrixes and determinants are called minor.
We follow a pattern of adding/subtracting by starting with positive and so the result will be a large sum that might include more sums inside. To calculate the determinant we can select any row or column we like and iterate through each element inside of this row or column.We start by multiplying the value of the first element with the determinant of an minor-matrix that doesn't contain the row and column this first element is in. We continue subtracting the second element times (product) the determinant of the minor-matrix that doesn't contain the row and column the second element is in. This continues on until we have no more element in the row/column. We then find the determinant of each minor matrix doing the same thing except if we are in an 3x3 matrix that we know a faster way that we will see in a sec.
Example:
So, the determinant of an 4x4 matrix when we start from the 1st row looks like this:

I found this example here.
Attention! The +- pattern starts from the top-left corner and continues going from row to row. So, if we try calculating the determinant of an 5x5 matrix starting from the second row than we will use an - first(+-+-+ for first row). This may not make sense now, but maybe the second row helps us later on, cause it gives us minor matrixes that are easier and so it is useful to know that this +- pattern in not per row, but has to do with the whole matrix row by row!
The determinant of an 2x2 matrix is simply
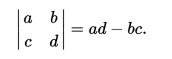
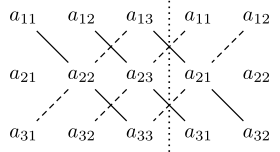
The determinant of an 3x3 matrix can be calculated using the rule of Sarrus. To use this rule we simply write an augmented matrix that contains our main matrix A and the first 2 columns repeated after A. We then find the sum of the products of the diagonals that go from the upper-left to the down-right corner, and subtract them with the sum of the products of the diagonals that go from the upper-right to the down-left corner.
The augmented matrix looks like this:
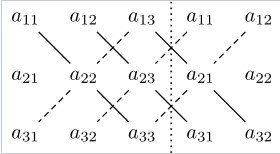
And so we have the following result:
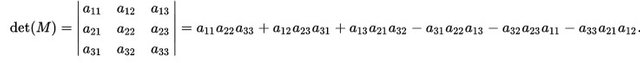
Determinant Rules:
We have some rules that are pretty useful sometimes. These are:
- When multiplying the elements of a single row or column then the determinant gets also multiplied by this number. This can be generalized having det (k*A) = k^n *A, where n is the numbers of rows/columns of A
- When having 2 equal (they could be in a ratio) rows/columns the determinant is 0 (det A = 0)
- When switching 2 rows/columns of a matrix the determinant changes sign (+ -> - and vise versa), and so when doing an odd number of switches the sign changes and when doing an even number of switching the sign doesn't change.
- The determinant doesn't change when doing elementary row/column addition (ri <-> ri +a*rj)
- When multiplying 2 matrixes the determinant of the result equals the product of the determinants of each matrix. det(A*B) = detA * detB
- A matrix is invertible only when the determinant is not 0!
- When a matrix is invertible then the determinant of the inverse matrix is the inverse of the first matrix. det A^-1 = 1/detA
- The determinant of the transpose matrix is equal to the determinant of the matrix we transposed
Adjoint matrix:
We specify a cofactor bij for each element aij of a matrix. This cofactor is equal to the determinant of the minor matrix that we get when removing the row/column the element is inside of the matrix with a sign that is specified by its posision. The position follows the +- pattern I talked about and so we have that:
bij = (-1)^(i+j)*det Aij, where i, j are the indexes and Aij is the minor matrix I told before.
The adjoint matrix is represented as adj(A) and contains all the cofactors of matrix A.
The inverse matrix can be found using the following:
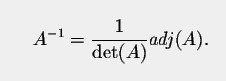
You can see that det(A) !=0 and now we know why a matrix with detA==0 can't be inverted.
Solving a Linear System using Determinants:
To solve a linear system using determinants we use the rule of Cramer. This rule tells us that if the determinant is non-zero then the system A*X = b has one solution X = (x1, x2, ..., xn) where:
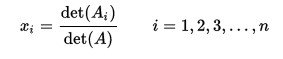
Ai is the matrix that we get when replacing the i-column with the column b of constant values.
When detA==0 then the system has no solutions or infinite solutions.
A special case are the homogeneous systems (A*X = 0) where we have 2 possible outcomes:
- when detA !=0 we have one solution that is the zero-solution
- when detA==0 we have infinite solutions that include the zero-solution
Possible Outcomes:
- From the rule of Cramer when detA != 0 the linear system has one unique solution
- detA==0 and the system is not homogeneous than we will have to use the Gauss method to find out if it has no or infinite solutions
Gauss Method Outcomes:
- When all elements except the most-right element (constant of b) in a row are 0 then we have no solutions, cause 0 != constant
- When the number of non-zero linear equations is less then the number of variables (n</li>
infinite solutions
- When the number of non-zero linear equations is greater or equal to the number of variables (n>=x) then we have one unique solution (this will not occur in square systems, cause we are using the Cramer method then)
The first means that if we find a row that looks like this:
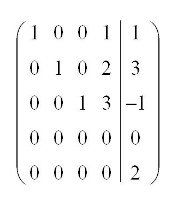
the linear system has no solutions, cause the last row has a constant == 0
In the same way if we find something like this:
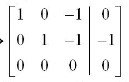
we have infinite solutions, cause we have more variables then linear equations.
Infinite Solutions:
To find how this infinite solutions look like we will select a variable or more to be a parameter or parameters and solve one of the equations having only the parameters and constants on the right. That way the variables that are not parameters will be found using a function that contains some parameter. The whole result will contain parameters and so we have infinite results.
Let's say that in the example I had before for infinite results we have the variables x, y and z. Then the first and second equation look like this:
x - z = 0
y - z = -1
z is common in both and so z will be our parameter and the value of z will be any real number.
That way we have x = z and y = z - 1
So, our solution is X =(z, z - 1), where z real
This last part is something that I forgot to talk about last time, but we managed to talk about it today and so we are now done with everything! Also, you can find a full-on example with Cramer here :)
And this is actually it and I hope you enjoyed this post!
Until next time...Bye!