Hello friends of steemit, continuing with my explanations about the science of mathematics, today I will speak in this post about the exponential function, its definition, the properties that make it up, the associated graphics, this function is very important since it allows us to model situations of real life, here also will be some examples of exercises where this function applies.
Exponential function
to exponential function, it is formally known as the real function ex, where e is Euler's number, approximately 2.71828; this function has as a domain of definition the set of real numbers, and has the peculiarity that its derivative is the same function. It is equivalently denoted as f (x) = ex or exp (x), where e is the base of the natural logarithms and corresponds to the inverse function of the natural logarithm.
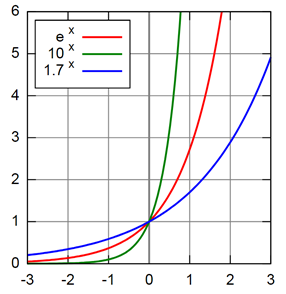
Exponential Function Chart
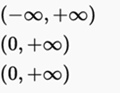
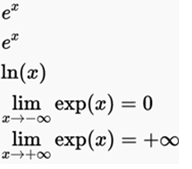
In much more general terms, a real function E (x) is said to be of the exponential type based on whether it has the form
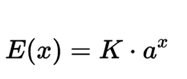
being a, K ∈ R real numbers, with a> 0, a ≠ 1. Thus, we obtain a range of exponentials, all similar, that depend on the base they use.
Definitions
The exponential function ex can be defined in several ways equivalent to each other, as an infinite series or as a limit of a sequence. In particular it can be defined as a series of powers:
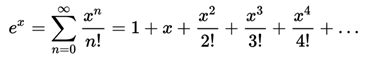
or as the limit of the succession:
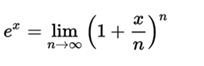
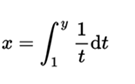
Properties
The exponential function (and exponentials in base other than e) satisfy the following general properties.
- They are the only functions that are equal to their derivative (multiplied by a constant, in case they have a base other than e)
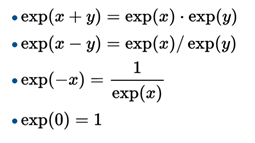
Derivative
The importance of exponential functions in mathematics and science lies mainly in the properties of its derivative. In particular,
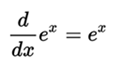
That is, ex is its own derivative. It is the only function with that property (without taking into account the multiplication of the exponential function by a constant). Other ways to express the above:
- The slope of the graph at any point is the height of the function at that point.
- The rate of increase of the function in x is equal to the value of the function in x.
- The function is a solution of the differential equation
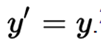
If the base of the exponential function is any real number greater than 0, then its derivative can be generalized like this:
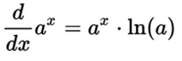
where the function ln (a) is the natural logarithm of a. In the particular case of a = e it turns out that ln (e) = 1 and therefore 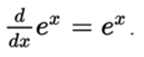
Complex exponential function
As in the real case, the exponential function can be defined as a holomorphic function in the complex plane in different ways, some of which are simple extensions of the formulas that are used to define it in the domain of real numbers. Specifically, the most usual way to define it for the domain of complex numbers is through the series of powers, where the real value x is replaced by the complex variable z:
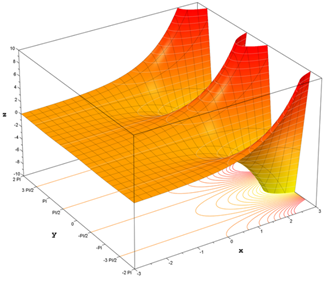
Graph of the real part of an exponential function in the field of complexes 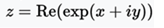
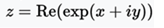
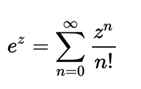
for pure imaginary values the identity is fulfilled
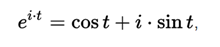
in which a particular case is the identity of Euler, connector of such important numbers as the one, the zero, e, pi number and the imaginary unit.
Using the previous identity, where now z = x + yi, with x and y real numbers, a definition equivalent to the first one is obtained,
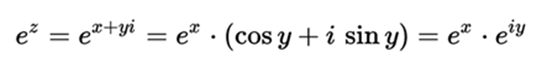
equation that shows that this function, besides being holomorphic, is periodic, with a period for the imaginary part of
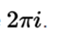
General exponential function
We have a fixed base = the complex number a different from e, and the exponent z which is a variable. With the indicated: the general exponential function w = f (z) = a is defined as:
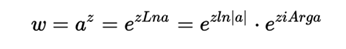
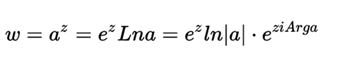
It is a family of univocal functions, not linked to each other, that are distinguished by the factors exp (2kπiz), where k is any whole number.
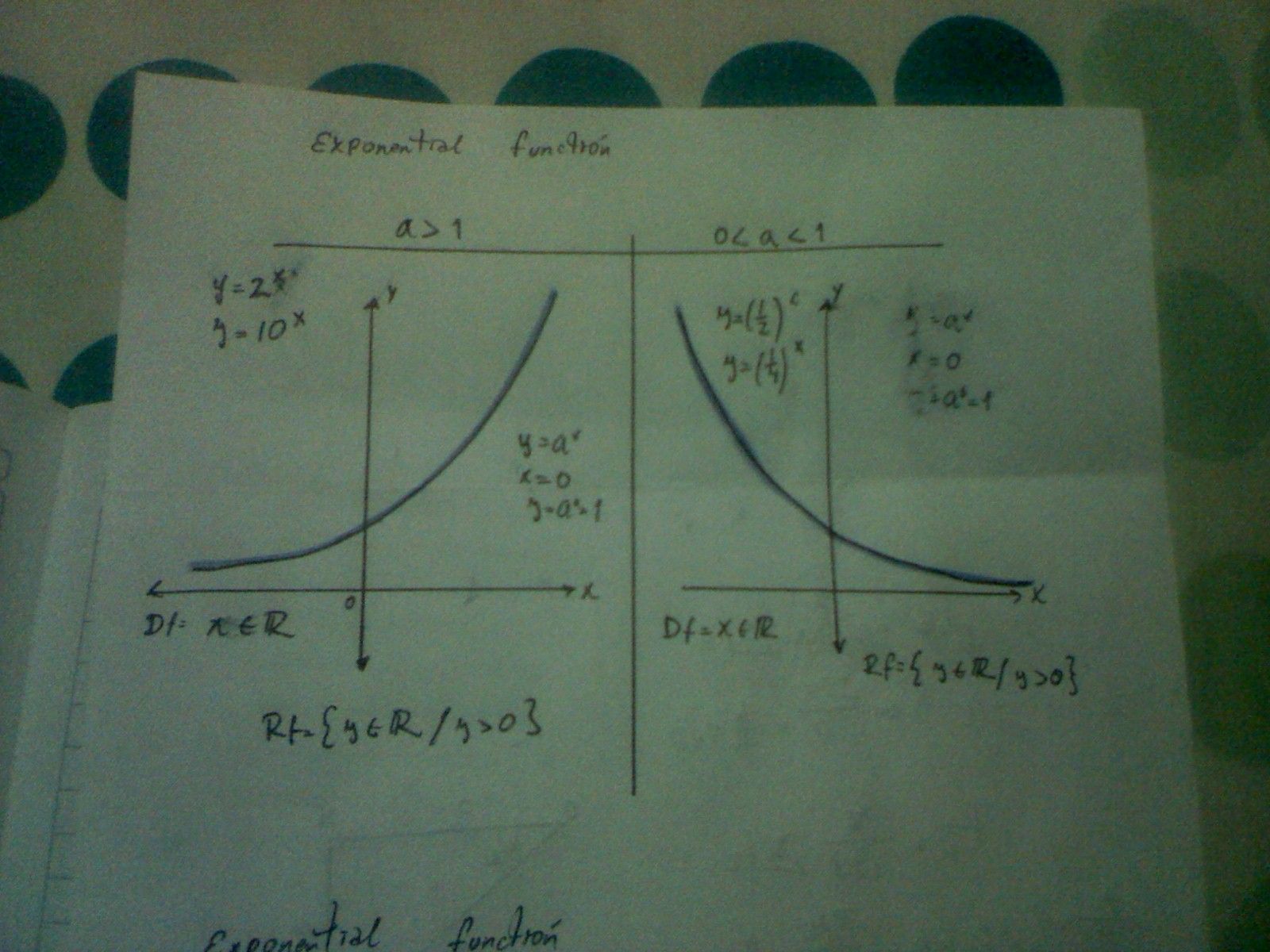
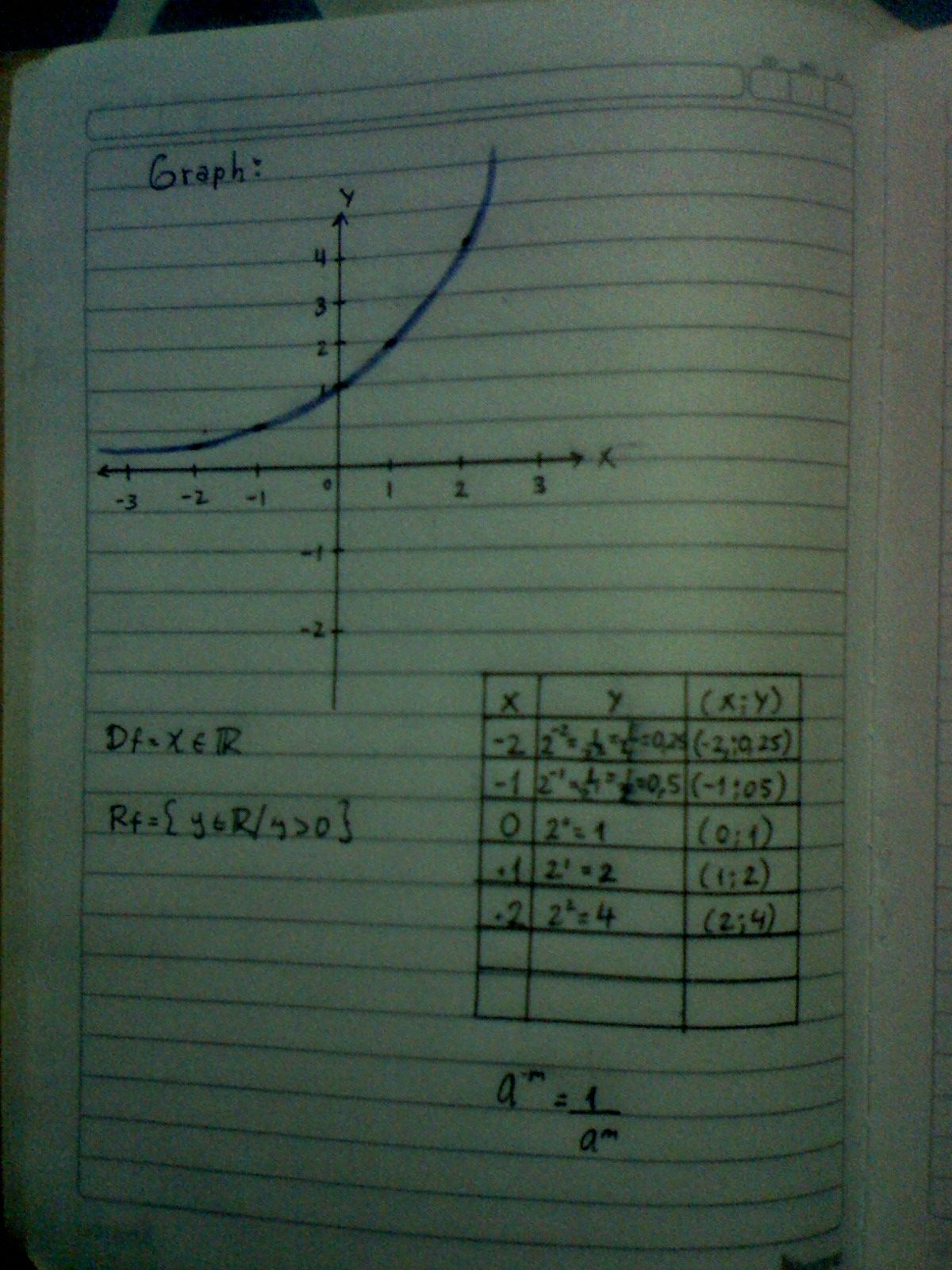
Below are examples of basic exercises, where the exponential function is applied, where the domain, the range is determined and the respective graph is represented.

Notes and references
1 . Gustafson. Intermediate algebra
2 . Haaser et al. Mathematical Analysis II
3 .Name used by the creative mathematicians: the North American Derryck, the Hungarian Polya and the Finnish Alfhors, etc.
4 . M. A. Lavréntiev / B. V. Shabat "Methods of the theory of functions of a complex variable, Editorial Mir Moscow (1991)
5 . Lavréntiev et al: cited work
Bibliography
Abramowitz, M. and Stegun, I. A .. Exponential Function. §4.2 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 69-71, 1972.
Courant, Richard and Fritz, John. Introduction to calculation and mathematical analysis Vol.I. Editorial Limusa, 1999.
Apostol, T. M., Calculus. Volume I. Calculation with functions of a variable, with an introduction to linear algebra. Editorial reverte, 2005
Ahlfors, Lars. Complex Analysis: an Introduction to the Theory of Analytic Functions of One Complex Variable (1953, 1966, 1979)
Well written, I am finding it more and more crucial that people know the characteristics of exponential functions and in particular the Taylor series expansion. I find many relevant use-cases for this in practice.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
thanks for your comment, a pleasure to make this kind of publications, I'm following you, I hope you can follow my explanations about math
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Great explanation bro but i dont understand complex mathematics !!!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Greetings friend, a pleasure to clarify all the doubts, thanks for your comment, I follow you, greetings.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I did follow you too.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
excellent post friend as always sharing your knowledge greetings
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Grear post! Hope to see more post about Math froM you... -A Math teacher here
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
hello friend greetings, if with pleasure every day I publish content about the science of mathematics, a pleasure that you follow me, I'll follow you, thank you for your comment.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I followed u already... My pleasure if u will follow back. Keep steeming...
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit