Hi, Steemers! This is my 5th post on Steemit and I'm very glad that you liked my previous post. I'm already thinking about the next dance tutorial. Today I want to tell you about one popular math object.
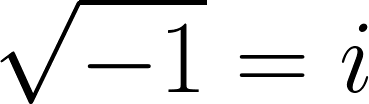
My basic concern of this post is to attract attention of the audience to the complex numbers and to show, complex numbers are not something difficult that can be figured out just by mathematicians; complex numbers are such a real thing.
I am sure, everyone of You has heard about complex numbers once or more times (a lot of people are coming them up at University ). But as far as I know, traditional ways of studying complex numbers field are too formal and they don't provide "visualisation".
Probably, this note , which I used to make for myself, will be useful for You.
Real Numbers and Actions
What are the real numbers ? Are a method of measure (3,5 kg of apples, 0,33 l of cola etc.)? Actually, numbers are not just numbers, but also operations of these numbers. We can sum and multiply numbers, and that let us describe them with actions.
For example, let's analize actions of real numbers for multiplication. Let x be a real number, we can treat it as oriented one-dimensional simplex (vector) with endpoint x.

After multiplying by 2, this vector will be twice longer. It is an action of number "2".

After multiplying by "-1", vector "turns around". It is a action of number "(-1)", so-called direction changing.

To sum up, these are actions of numbers. Now You understand , that "actions" of numbers can be visualised.
Therefore we can prolong vector and change its direction to opposite. This is real numbers.
Less Limits
What would be if we stop limiting ourselves using only one dimension? What would be if to add second dimension? And what is it two-dimension numbers? Let's say that number is a vector with endpoint in some point of plane (x).
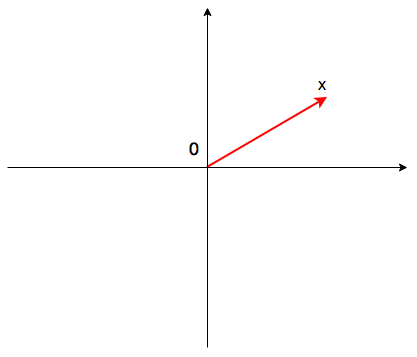
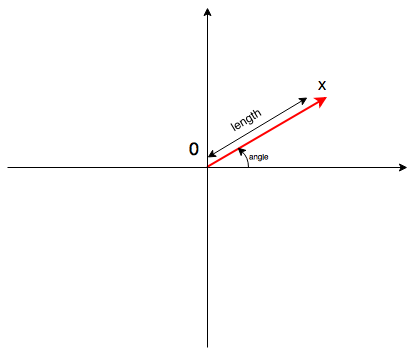
How to get along with operations of this kind of numbers? Firstly, let's decide, how we can describe numbers on plane. We can use Cartesian coordinate system but now more comfortable to use Polar coordinate system. Polar systems are using two magnitudes: length of vector and an angle.
Secondly, let's think how we can define interaction of numbers X and Y.
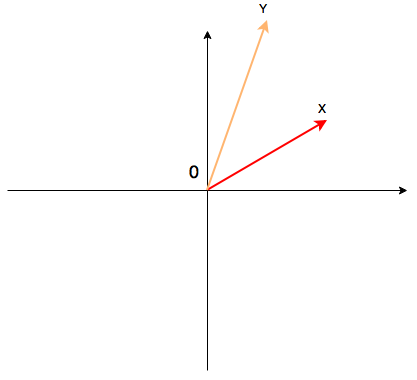
Remember, interaction of two numbers must result a number. What kind of number? Each arguments has an angle and length. Let interaction of two numbers Z=XY result such a number, that its length is equal to multiplication of length of operands, and its angle is equal to sum of angles:
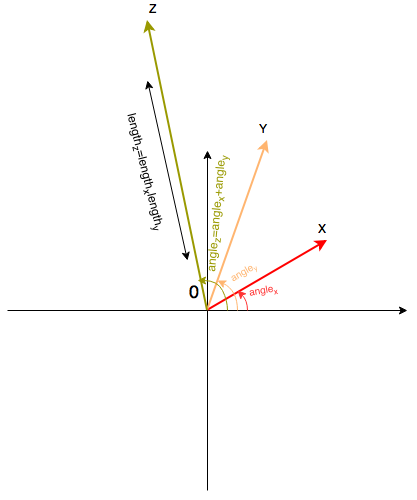
Actually, we have just made complex numbers. It's left to define sum of 2 numbers. It defines as sum of two vectors (the parallelogram rule).
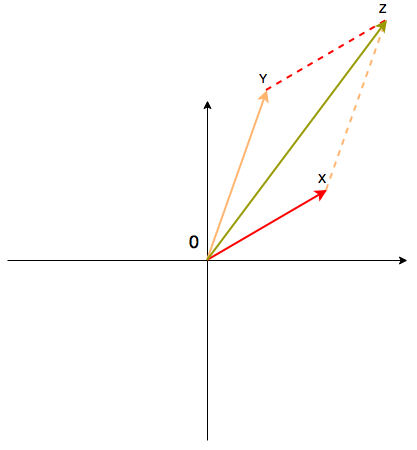
Now we have complex numbers. The plotting, which were given above, is geometrical plotting. Any complex number can be written down this way
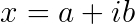
where a and b are vector coordinates on a plane.
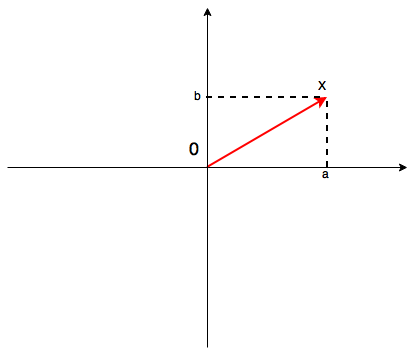
This kind of definition lets us easy to see complex numbers not just change its length (as the reals do), but also turn around! Therefore we can use them as an instrument for encoding the turns. Quarter-turn exactly is number i ( unit imaginary number).
Rotations
As I said, multiplication by a complex number takes a turn and prolongation. The set of complex numbers with length equal to one completely specify all possible turns.
If you go further, you can define a quaternions - four-dimensional numbers. They set the rotations in space. Moreover, they are used in navigation systems!
I hope you've enjoyed it,
Kate.
Вступайте в ряды Фурье!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Приятно видеть русскоговорящих, особенно знакомых с математическим юмором)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Complex numbers are not vectors.
It could be presented as vector (or as matrix).
Complex numbers are just a way to have a powerful tool for polynomials algebra.
Really, when we talk about "i", we talk about polynomial "x^2+1=0".
And when we use polynomials, we usually use complex numbers, and interpret 'em like frequency (in transfer function) or angular (polar system) or something else.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yes, you're right. It's just simple and useful to present our complex number like a vector. You can easily understand how to work with it this way. But they were ctreated to expand defenition of number.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Your 5th post...or story?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Of course, it's my 5th story. Anyway comments and posts are not the same things for me.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for the post :) I just recognize school program :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Oh, your school was rather cool) Russians Middle School curriculum are not includes complex numbers.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Quaternions are paltry objects. Octonions are even cooler!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@complexring can answer you that, he is a good mathematician.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
also must be mentioned but complex numbers are heavily used in anything related to electricity/electronics
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
coplex numbers
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit